INTRODUCCIÓN
Se estima que hay 232 millones de inmigrantes internacionales a nivel mundial1, de los que 76 millones viven en Europa, un tercio del total mundial2. Al margen del impacto social, económico y político de los movimientos migratorios en los países receptores y emisores, el impacto en la salud de las personas emigradas es de gran relevancia en salud pública. Diversos factores individuales (procedencia, cultura, decisión de migrar) y del entorno (recursos, opciones laborales), entre los que figura la actividad laboral, se apuntan como relevantes determinantes de la salud3, igualmente si se tiene acceso a la atención sanitaria4.
En España, una reciente revisión bibliográfica de artículos originales sobre inmigración y salud, publicados entre 1998 y 2012, señala que solo el 28% de los estudios tiene un diseño de cohortes, mientras que el 56% tiene diseño transversal, siendo insuficiente para describir el patrón epidemiológico y el proceso migratorio5. Estudiar el proceso migratorio y su impacto en la salud supone retos relacionados con la ausencia de criterios homogéneos en la definición de inmigrante, el sesgo de selección, el escaso tamaño muestral o la dificultad de reclutamiento6,7,8,9. Se ha descrito que los estudios con estrategias comunitarias de aproximación, en los que personas clave de las redes de migrantes apoyan el reclutamiento y que los estudios de cohorte que incluyen familias inmigradas tienen mayores tasas de participación y retención6,10. Son escasos los estudios longitudinales sobre inmigración y salud que consideran las características del entorno familiar, posiblemente debido a la dificultad que el propio proceso migratorio impone en las formas de familia, de escasa homogeneidad en el uso, clasificación y delimitación del concepto de familia10,11.
Desde mediados de los años 80, España se caracterizó por un incremento exponencial de la población inmigrante extranjera que se detuvo e incluso disminuyó en el año 2009, aunque desde 2013 ha vuelto a incrementarse ligeramente. En 2014, el saldo migratorio fue negativo a pesar de que la inmigración aumentó un 9,4% respecto a 201312. Aunque los datos absolutos muestran que la población extranjera residente en España sigue disminuyendo cada año, también se debe a que muchos de ellos adquieren la nacionalidad española. Durante 2015, 114.207 personas adquirieron la nacionalidad, el 2,56% de la población extranjera residente en este año12.
En 2014, las personas inmigrantes residentes en España (10% de toda la población), procedían sobre todo de Marruecos (15,4%), Ecuador (4,6%), Colombia (3,7%) y China (3,5%) entre los países de fuera de la Unión Europea12. Se caracterizan por ser jóvenes y activos, con un objetivo migratorio predominantemente económico y, alrededor del 50%, viven en familias que conviven con los hijos12,13,14.
El Subprograma Inmigración y Salud (SIS) del Consorcio de Investigación Biomédica de Salud Pública (CIBERESP) tiene como propósito estudiar la magnitud y la distribución de los problemas de salud en la población inmigrante de España así como sus determinantes, con el fin de contribuir a la mejora de su estado de salud e informar las políticas sanitarias y a la investigación aplicada dirigidas a esta población. En el marco del SIS, en el año 2014 se constituyó el Proyecto de Estudios Longitudinales de Familias Inmigrantes (PELFI) como un estudio de cohortes multicéntrico de familias inmigradas. La vocación del PELFI es poder incluir cohortes de distintas ciudades españolas que tengan como unidad de estudio la familia y que compartan información común para estudiar la historia e impacto del fenómeno migratorio en la salud.Así mismo, el estudio PELFI plantea incluir objetivos específicos relacionados con el ámbito de experiencia de los grupos participantes. Actualmente, el estudio PELFI incluye sub-cohortes en Alicante), Barcelona y Badalona/Santa Coloma de Gramanet y sus objetivos generales son : 1.- Describir el estado de salud de las familias inmigradas y su eventual evolución con el tiempo; 2.- Estudiar la evolución de los determinantes estructurales relacionados con la experiencia migratoria y la familia y su impacto en la salud; 3.- Analizar las condiciones de empleo y la evolución de su influencia sobre el estado de salud física y mental y 4.- Describir y analizar los factores conductuales y estructurales asociados a los problemas de salud mental. En las tres sub-cohortes la unidad de estudio son las familias, entendidas como unidades domésticas, incluyendo también los hijos e hijas de los migrantes, se incluyen las nacionalidades más prevalentes en cada ciudad y se cuenta con un grupo de familias control autóctonas.
El objetivo del presente artículo es describir el trabajo de campo basal y las principales características socio-demográficas de las familias incorporadas a las sub-cohortes de Alicante y Barcelona.
METODOLOGÍA
En 2014, año de preparación del proyecto PELFI, el municipio de Alicante registraba 332.067 habitantes empadronados, de los cuales el 18,3% eran nacidos en el extranjero. El municipio de Barcelona contaba con 1.602.386 habitantes de los cuales el 21,7% de estos nacidos fuera de España15. Para este estudio se seleccionaron los barrios de Zona Norte de Alicante y Nou Barris de Barcelona, dos barrios de características socioeconómicas similares y con alto porcentaje de inmigrantes, comparado con el total de sus respectivos municipios15.
La población de este estudio está constituida por familias inmigradas y autóctonas. Se delimitó la definición de familia utilizada en la Encuesta Nacional de Salud 2011-201216: Personas que ocupan una vivienda o parte de ella, comparten un presupuesto y consumo común (comparten alimentos u otros gastos relevantes con cargo a dicho presupuesto) y llevan viviendo juntos al menos seis meses en el momento del reclutamiento. Los criterios de selección de las familias incluyeron tener al menos un hijo de entre 12 y 17 años, al menos un adulto de entre 18 y 65 años nacido en Colombia, Ecuador, Marruecos o España y que hubiera trabajado un total de un año en España, no necesariamente de forma continuada. En los casos de familias biparentales ambos progenitores/tutores debían haber nacido en el mismo país. Debían tener expectativas de permanecer en España, por lo menos 18 meses después de haber sido selecionados. Solo se incluyeron en la muestra las familias en las que se entrevistaron a todos los sujetos de interés que cumplían los criterios de selección.
Muestreo y selección. Para la selección se utilizaron técnicas no probabilísticas. Se empleó principalmente la selección de conveniencia, el sistema de bola de nieve y la captación en lugares diana. Se usaron diferentes aproximaciones para reclutar a la población de estudio. Por una parte se realizaron reuniones con los agentes de mediación e informantes claves de los barrios. Estos se pusieron en contacto con las familias y, con su permiso, proporcionaron el contacto a los encuestadores. Por otra parte, para captar “a puerta fría” se visitaron lugares diana como centros escolares, centros de salud, plazas, iglesias o bares.
El cálculo del tamaño muestral para las dos sub-cohortes se definió como una muestra de 180 familias de padres nacidos en Colombia, Ecuador y Marruecos y se incluyó el grupo control con 50 familias autóctonas. Finalmente, se reclutaron un total de 250 familias, 193 inmigrantes y 57 autóctonas, incrementando el tamaño muestral en un 9% en prevención de las posibles pérdidas durante el seguimiento.
Recogida de datos. El trabajo de campo comenzó en junio de 2015. La recogida de la información se realizó por encuestadores con experiencia en trabajos con población inmigrante. En total intervinieron 16 encuestadores, 6 nacidos fuera de España, 13 mujeres (81,3%). Se llevó a cabo un protocolo común de instrucciones y se realizaron talleres/reuniones en ambas ciudades.
Los cuestionarios fueron diseñados ad hoc, uno con 112 preguntas para los adolescentes de 12 a 17 años y otro con 97 preguntas para las personas adultas, ambos con una duración estimada de alrededor de 30 minutos8. Se elaboraron a partir de otros cuestionarios -ITSAL17 y MICASA11- y los de las Encuestas Nacionales -ENS16 y ENCT18-. En ambos el 95% de las preguntas fueron cerradas. El equipo investigador organizó talleres con trabajadores de instituciones de salud, laborales y organizaciones no gubernamentales con los objetivos de identificar contenidos clave en la temática de estudio y mejorar los cuestionarios. Finalmente, para esta fase del trabajo de campo basal, se preguntaron cuestiones sobre características sociodemográficas y familiares, proceso migratorio, apoyo social, condiciones de trabajo y empleo, salud mental y comportamientos de riesgo. Si alguna persona de la familia cumplía los criterios y no aceptaba participar, se descartaba incluir a esta familia en el estudio, por lo que no se incluyeron familias parcialmente entrevistadas19.
Los cuestionarios se pueden consultar en la siguiente direccion web del proyecto: http://www.ciberesp.es/programas-de-investigacion/subprogramas-estrategicos/subprograma-inmigracion-y-salud-ciberesp-sis-ciberesp
Se realizó un estudio piloto con 18 familias, con el fin de afinar la calidad de los contenidos y asegurar la comprensión de las preguntas. Se mejoraron un total de 19 preguntas. Las encuestas fueron administradas mediante tabletas en Barcelona y con los cuestionarios impresos en Alicante. El control de calidad de la recogida de datos consistió, por un lado, en la supervisión directa en campo y, por otro, en la supervisión mediante la comprobación simultánea que ofrecen las tabletas y comprobación mediante llamadas telefónicas a algunos encuestados para verificar que habían respondido la encuesta.
Las entrevistas se realizaron en los domicilios, asociaciones y lugares públicos, entre otros, ofreciendo a las familias flexibilidad para elegir el lugar y la hora de la entrevista. Cuando el diseño de la escala lo requería, las preguntas fueron auto-administradas.
El proyecto fue aprobado por el comité ético de a la Universidad de Alicante y del Instituto de Recerca del Hospital Universitario Vall d’Hebrón. Se anonimizaron los datos, asegurando la confidencialidad de acuerdo a la Ley Orgánica 15/1999 de Protección de datos de Carácter Personal20. Los encuestados firmaron el consentimiento informado, previa explicación del proyecto y del cuestionario.
Análisis estadístico. Se realizó un análisis estadístico descriptivo de las variables que conforman las características de las familias y de los adultos y adolescentes como unidades en sí mismas.
Se calcularon la tasa de cooperación, dividiendo el número de familias entrevistadas (F) entre F más el número de familias contactadas que cumplían los criterios de inclusión pero que se negaron a participar (FC): F/F+FC. La tasa de distribución de respuesta, dividiendo F entre la suma de F más FC más familias contactadas que no cumplían los criterios de inclusión (FNC). Y la velocidad de reclutamiento, dividiendo F entre el tiempo que duró el trabajo de campo (bien en número de días bien en número de meses), basándonos en las definiciones de la Sociedad Americana para la Investigación de la Opinión Publica de 201619. Para el análisis estadístico se utilizó el programa Stata 14.
RESULTADOS PRELIMINARES DEL TRABAJO DE CAMPO
El trabajo de campo basal corresponde a la fase en que se reclutó a las familias participantes, primera obtención de información de la cohorte. La tasa de cooperación fuedel 82,0%, la tasa de distribución de respuesta fue del 72,9% y la velocidad de reclutamiento de 38,5 familias mensuales (1,3 familias diarias) en los 6,5 meses que duró el trabajo de campo en total en Alicante y Barcelona.
El 67,9% de las familias fueron reclutadas mediante la técnica de muestreo de conveniencia, el 29,7% mediante el sistema de bola de nieve y solo el 2,4% fueron captadas en lugares diana. Por municipalidad, el muestreo por conveniencia representó el 95,9% en Alicante y el 40,9% en Barcelona.
El 71,1% de la encuestas se realizaron en los domicilios de las familias. El 27,3% en instalaciones de asociaciones, ONGs y otros lugares prestados por entidades colaboradoras. El 1,6% se realizaron en lugares públicos, como bares, plazas o bibliotecas.
La encuesta más corta duró 6 minutos y la más larga 116 minutos, con una media de casi 25 minutos y una desviación estándar (DE) de 10,7. El 57,2% de las familias fueron entrevistadas por la tarde (de 16:00 a 19:59 horas), el 17,6% a medio día (12:00-15:59), el 14,4% por la noche (20:00-24:00) y el 10,8% por la mañana (08:00-11:59).
En Alicante, la tasa de cooperación fue del 91,7% y la de distribución de respuesta del 85,3%. La supervisión directa en campo fue del 15% y el control de calidad telefónico del 10,5%. Las entrevistas a personas adultas duraron una media de 28 minutos con una DE de 9,1. La más corta duró 10 minutos y la más larga 60. El 52,7% de las entrevistas se hicieron en horario de tarde (16:00h-19:59h).
En Barcelona se obtuvo una tasa de cooperación del 74,4% y una de distribución de respuesta del 64,0%. El sistema de control de calidad consistió en utilizar una hoja de Google compartido, con todas las citas, para que el equipo de investigación pudiera asistir a las entrevistas aleatoriamente y la comprobación simultánea que ofrecía el uso de la tableta permitía comprobar que la entrevista se estaba realizando en el lugar y en la hora programada. Las entrevistas en personas adultas duraron una media de 22 minutos, con una DE de 11,1. La más corta duró 6 minutos y la más larga 116. El 51,0% de las entrevistas se hicieron en horario de tarde (16:00h-19:59h).
Características sociodemográficas de las familias reclutadas. En total se reclutaron 250 familias, 82 procedentes de Ecuador, 82 de Colombia, 29 de Marruecos y 57 españolas (tabla 1). De ellas 152 (60,8%) se identificaron como biparentales. El 98,8% de las familias se componían de 2 a 5 miembros. El 49,6% convivía con otra familia que no pertenecía al mismo hogar, pero que vivía en la misma vivienda, caso que se daba más en Barcelona (62,5%) que en Alicante (36,1%; p<0,001). En el 48,0% de las familias había un menor de 18 años y en el 35,2% había dos, siendo el 16,8% las que tenían 3 o más menores.
Tabla 1. Características de las unidades familiares en las subcohortes de Alicante y Barcelona. PELFI, 2015

La tabla 2 muestra las características sociodemográficas de las 473 personas adultas encuestadas. Se entrevistó a más mujeres que hombres (59,8% frente a 40,2%). El 56,7% de las personas adultas tenía estudios de secundaria. Se hallaron diferencias estadísticamente significativas entre las sub-cohortes respecto a la variable de nivel estudios (p<0,001). En Alicante, el 30,9% de las personas adultas no tenía estudios o tenía estudios de primaria comparado con el 16,6% en Barcelona, ciudad que a su vez tuvo mayor porcentaje de adultos con estudios universitarios, el 27,3%, frente a Alicante con un 11,8%. El 68,8% de la cohorte estaba empleada la semana anterior a la de realización de la encuesta.
Tabla 2. Características sociodemográficas de las personas adultas (18 a 65 años) en las subcohortes de Alicante y Barcelona. PELFI, 2015
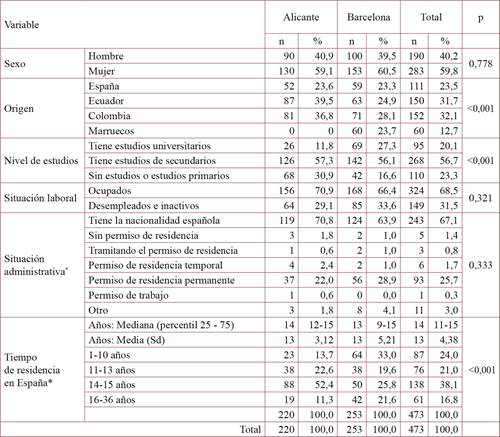
El 76,5% de personas adultas nacieron fuera de España y todas tenían tarjeta sanitaria. El 67,1% tenía la nacionalidad española y el 25,7% tenía permiso de residencia permanente. Llegaron al país entre 1979 y 2014 y llevaban una media de 13 años en España en el momento de la entrevista, con una desviación típica de 4,38.
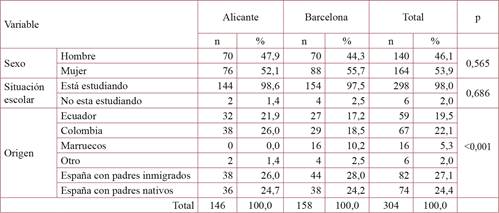
Como muestra la tabla 3, se entrevistó a 304 adolescentes de entre 12 y 17 años de edad. El 53,9% eran mujeres y el 98,0% estaba estudiando. El 27,1% de los adolescentes nació en España pero pertenecían a familias inmigradas, es decir, que sus padres nacieron fuera de España, y el 24,4% eran del grupo que nació en España de padres españoles.
COMENTARIOS
Por lo que sabemos hasta ahora, este es el primer proyecto longitudinal multicéntrico realizado en España para el estudio del proceso migratorio y la salud, en el que se entrevista a varios miembros dentro de cada familia.
Los resultados de este trabajo muestran que la tasa de cooperación, que resulta muy elevada, indica que el sistema de reclutamiento empleado es muy útil para este tipo de estudios. Un estudio previo, realizado en varias ciudades españolas, con selección de conveniencia de más de 2.000 inmigrantes, tuvo una tasa de cooperación del 53,4% (no incluye familias)8. Otro estudio de revisión, muestra que se obtienen mejores resultados cuando la selección es de conveniencia y el tamaño muestral es menor a 500, con tasas superiores a 88%, aunque tampoco incluye familias como población de estudio10. Por tanto, la estrategia no probabilística de aproximación comunitaria, es decir, el asesoramiento, cooperación y confianza con los informantes clave, combinado con un bajo tamaño muestral, son dos factores que podrían explicar estos resultados positivos del trabajo de campo basal en nuestra investigación6,8,10, que permitió además superar el número de familias estimadas en el diseño.
Aunque desconocemos la magnitud del sesgo de reclutamiento y participación y, por lo tanto, se debe evitar generalizar los resultados a toda la población migrada, el proyecto fue diseñado para explorar asociaciones y generar información útil respecto a los procesos de reclutamiento y también de la salud y sus determinantes en familias inmigradas de características similares. Si bien las técnicas probabilísticas de reclutamiento permiten establecer muestras representativas, suelen adolecer de tasas muy bajas de participación cuando se trata de población inmigrante por lo que, para investigar inmigración y salud el sistema de muestreo probabilístico tampoco asegura una muestra representativa como ya se ha descrito en estudios previos6,8,9,10.
En este trabajo, más de la mitad del muestreo fue por conveniencia, lo que podría sugerir un sesgo de reclutamiento de una mayoría de familias integradas en red social y extra familiar (acuden o participan en asociaciones, ONGs, iglesias, centros escolares, entre otros), y se podría suponer que se excluyó a familias en peores condiciones socioeconómicas o con menor presencia en determinadas redes sociales de apoyo. Sin embargo, la aproximación de técnicas de conveniencia y bola de nieve permite llegar a casi toda la comunidad cuando, como se ha dicho, se tiene la confianza de los informantes clave, caso más acusado en Alicante.
La experiencia previa de los encuestadores y la flexibilidad y facilidades que se ofrecieron a las familias para ser encuestadas favoreció las elevadas tasas de respuesta. Algunas diferencias entre Alicante y Barcelona, como la duración del trabajo de campo basal, podrían explicarse por ejes de desigualdad como el sexo y la procedencia, es decir, por el hecho de que solo en Barcelona se reclutaron familias de origen marroquí. En España, Delclós et al. describieron que los inmigrados procedentes de marruecos suponen más dificultades de reclutamiento que los de otros países de origen, especialmente cuando son mujeres8. En la sub-cohorte de Barcelona solo se contó con una traductora-entrevistadora de origen marroquí. Como encontró Aroian et al. en un estudio previo, posibles barreras idiomáticas, culturales o de carácter religioso podrían haber influido en estos resultados21.
Hasta el momento, en estudios similares3,6,8,10,22, o tienen otras técnicas de selección de participantes o siguen otros criterios, impidiendo la comparación de resultados descriptivos de características sociodemográficas entre ellos. Haber seleccionado solo tres países de nacimiento extranjeros, Ecuador, Colombia y Marruecos, constituye una limitación, no solo por el tamaño muestral. Se eligieron por tener mayor presencia en España, teniendo en cuenta las limitaciones de presupuesto, que reducía las posibilidades de incluir, además, a personas inmigradas de otros países, que también la tienen pero que, además, en muchos casos carecen del nivel suficiente de castellano para realizar la entrevista.
Los datos presentados sugieren que la realización de estudios longitudinales en población inmigrada en España es viable si se cuenta con los recursos adecuados, pero sobre todo aporta información clave para el diseño y mejora de las correspondientes estrategias de reclutamiento para este tipo de cohortes. La próxima descripción de los resultados basales de la sub-cohorte de Badalona/Santa Coloma de Gramanet y especialmente el análisis conjunto del seguimiento de estas familias, así como el aumento de la población de estudio mediante la incorporación de otras ciudades al Proyecto PELFI, permitirá identificar los determinantes no solo de participación sino también de adherencia a los estudios longitudinales por parte de población migrada y empezar a describir cómo influye el proceso migratorio en las salud de estas familias a lo largo del tiempo. La actual situación migratoria en España y en el resto de Europa hace más pertinente que nunca que la investigación en salud pública incorpore y financie este tipo de investigaciones.