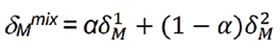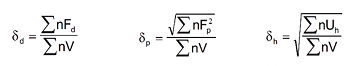Highlights
Partial solubility parameters were used to research the dissolution behaviour of barnidipine in seventeen mono-solvents.
Partial solubility parameters were calculated by applying theoretical group contribution methods, proposed by Hoftyzer-Van Krevelen and Fedors.
Miscibility and solubility behaviour were revealed by Hansen solubility parameters
The solvent effect was discussed by KAT-LSER model in seventeen mono-solvents.
Introduction
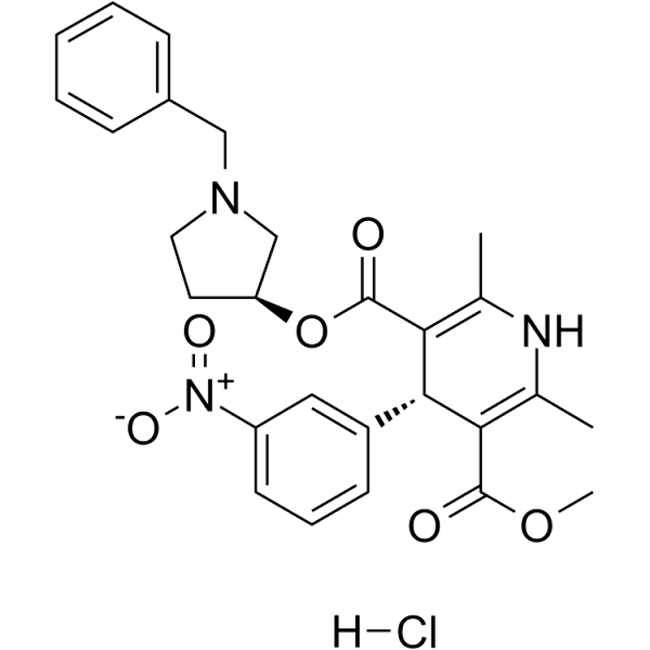
Barnidipine (Fig. 1, 3-(3S)-1-benzylpyrrolidin-3-yl 5-methyl (4S)-2,6-dimethyl-4-(3-nitrophenyl)-1,4-dihydropyridine-3,5-dicarboxylate) (CAS 104713-75-9, molecular formula C27H29N3O6 and molar mass 491.544 g/mol) is an antihypertensive drug that belongs to the group of dihydropyridine (DHP) calcium antagonists (Figure 1). Barnidipine has selective action against cardiovascular calcium antagonist receptors and its antihypertensive action is related to the reduction of peripheral vascular resistance secondary to its vasodilator action. As with other DHP calcium antagonists, vasodilator adverse events such as headache, flushing and peripheral edema account for most adverse events reported with its use and are generally transient. Barnidipine contains two chiral centres thus can have four possible enantiomers. The active component is composed of a single optical isomer (3’S. 4S configuration), which is the most potent and longest acting of the four enantiomers.1
The solubility and other physicochemical data of drugs in pure solvents play an important role in the process of drug discovery and the development of future formulations. Barnidipine belongs to class II of the Biopharmaceutical Classification System (BCS).2 In this study, the solubility of barnidipine in 17 pure solvents, which are widely used in the pharmaceutical industry including manufacturing and purification, was measured at 298.15 K and p = 0.1 MPa. The classical flask-shaken technique has been used as the solid-liquid equilibrium method to evaluate the solubility of barnidipine.3
In addition, the calculation of Hansen solubility parameters (HSP) was proposed, key to help in the design of drugs.4-6) Hansen divided the cohesive energy density (the square root of cohesive energy density is called solubility parameter, δ) into contributions from nonpolar interactions (van der Waals dispersion forces), dipole interactions and hydrogen bonding (Equation 1). HSP can be used for polar and hydrogen bonding systems to evaluate the compatibility of substances. Hansen solubility parameters (HSP) may be useful for preparing drugs and to estimate their miscibility.6
where the terms δd, δp, and δh are partial parameters representing the dispersion, polar and hydrogen bonding components of the total solubility parameter δT . The value of δd of a given solvent was assumed to be equal to that of a non-polar substance (e.g. hydrocarbon) of about the same chemical structure.
Furthermore KAT-LSER model had been applied to explore the solvent effects on barnidipine based on linear solvation energy relationships concept.7-9
Methods
Materials
Barnidipine (mass fraction purity > 0.999) was supply from Laboratorios Liconsa (Spain). 1,4-Dioxane, acetone, benzene, isopropyl myristate, N,N-Dimethylformamide (DMF), acetophenone, ethyl acetate, water, chlorobenzene, methanol, ethanol, 1-Octanol, 1-Pentanol, acetonitrile, 1,2-Dichloroetane, acetic acid, were acquired from Sigma Aldrich Co. (USA) and diethylene glycol monoethyl ether (DEGME, Transcutol® HP). The detailed properties regarding materials are listed in Table 1.
Table 1. Properties of solvents used in the present study.
| Chemical name | CAS Number | Molecular formula | Molar mass (g/mol) | Source | Purity mass fraction |
|---|---|---|---|---|---|
| Ethanol | 64-17-5 | C2H5OH | 46.07 | Sigma Aldrich | ≥99.9% |
| Water | 7732-18-5 | H2O | 18.02 | Millipore | ≥99.9% |
| Ethyl acetate | 141-78-6 | C4H8O2 | 88.11 | Merck | 99.5% |
| 1,4-Dioxane | 123-91-1 | C4H8O2 | 88011 | Sigma Aldrich | 99.5% |
| Acetic acid | 64-19-7 | CH3COOH | 60.05 | Sigma Aldrich | 96.0% |
| 1-Pentanol | 71-41-0 | C5H12O | 88.15 | Sigma Aldrich | ≥99.9% |
| DMF | 200-679-5 | C3H7NO | 73.09 | Sigma Aldrich | 99.8% |
| Benzene | 71-43-2 | C6H6 | 78.11 | Sigma Aldrich | 99.8% |
| DEGME | 111-90-0 | C6H14O3 | 134.17 | Gattefossé | 99% |
| Acetone | 67-64-1 | C3H6O | 58.08 | Merck | ≥99.5% |
| Chlorobenzene | 108-90-7 | C6H5Cl | 112.56 | Sigma Aldrich | ≥99.5% |
| 1-Octanol | 111-87-5 | C8H18O | 130.23 | Sigma Aldrich | ≥99.0% |
| Acetophenone | 98-86-2 | C8H8O | 120.15 | Sigma Aldrich | 99% |
| Isopropyl alcohol | 67-63-0 | C3H8O | 60.10 | Sigma Aldrich | ≥99.5% |
| Methanol | 67-56-1 | CH3OH | 32.04 | Merck | ≥99.9% |
| Acetonitrile | 75-05-08 | CH3CN | 41.05 | Merck | ≥ 99.8 % |
| 1,2-Dichloroethane | 107-06-2 | C2H4Cl2 | 98.96 | Sigma Aldrich | ≥99.0% |
Calculation of partial solubility parameter
The Hansen solubility parameters (HSP) are physicochemical parameters and are widely used to estimate the type of interactive forces drug-solvent, corresponding to atomic dispersion (δd), molecular dipolar interactions (δp), and hydrogen-bonding interactions (δh) (Equation 1). Hydrogen bonding is used here in a general sense to mean highly polar, oriented interactions of specific donor acceptor types.(10-11
HSP was used to estimate the miscibility of solvent and solute.12-14 The HSP for solvent mixtures (δMmix) is estimated through Equation 2:
the parameter α represents the volume fraction composition of cosolvent in the selected solutions; δ1M and δ2M express the HSP of cosolvent and water, correspondingly.
To evaluate the interactions of ‘‘solvent and drug” molecules, the solubility parameter (Δδ)15 (Equation 3) is employed here to illustrate the mixing procedure between solute and solvents.15
It has been observed that the Δδ value of <5.0 MPa1/2 indicates the high miscibility possibility between solute and liquid solvent.16
Bustamante et al.17-18 found that it is possible to directly regress lnX2 against the three partial solubility parameters, improving the significance of the regression coefficients. The modified models are presented as:
Equation 4 can also be used to calculate the partial solubility parameters of the solute using the ratio of the coefficients in expressions equivalent to the following:
δd2 = - (C2 /2C1 )
δp2 = - (C4 /2C3 )
δh2 = - (C6 /2C5 )
The HSP can as well be estimated from group contribution methods.19-22 The group contribution methods are only approximate, but they are very convenient to obtain a quite idea about the magnitude of the solubility parameters of a drug. The partial parameters are estimated from:
where Fd, Fp and Uh have been determined by Hoftyzer-Van Krevelen19-22 and Fd represents the contribution to the dispersion force; Fp stands for the contribution to the polarity force; and Uh stands for the contribution to the hydrogen bond interaction energy.
Solid-state characterization methods of barnidipine
Differential scanning calorimetry (DSC) (DSC 3, Mettler, Switzerland) was used to determine the melting temperature and the enthalpy of fusion of barnidipine. Approximately 5 mg was added in an aluminum hermetic pan with pin-holed lids, which were subsequently crimped. Indium was used as a standard substance during the calibration process. The test temperature ranged from 303.15 K to 573.15 K and the heating rate was 10 K/min under the protection of nitrogen. At least 3 separate DSC measurements were performed on each solid preparation.
Solubility measurements of barnidipine
The shake-flask technique was applied to measure the solubility of barnidipine in the seventeen mono solvents at 298 K. Excess amount of drug was collocated in flask of 100 mL and introduced into a thermostatized bath (±0.1 K) (HETO® Type SBD50-1 bio. Paris, France) shaking continuously at constant highest temperature to obtain the equilibrium of solubility at least three days (during this time, the mixture was checked at intervals to ensure the solid-liquid equilibrium). The main principle of the experimental equipment is to ensure stirring and dissolving of solute to reach saturation under a constant temperature. Once reached the equilibrium, samples of the saturated solutions were filtered (Durapore membranes 0.2 µm pore size, Darmstadt, Germany) and diluted with absolute ethanol. The concentrations were determined in a single beam spectrophotometer (Agilent® 61030AX. CA. United States) at λmax = 358 nm. The densities of the solutions were measured at each temperature in 10-mL pycnometers, to convert the molar solubility into mole fraction units.
All solubility measurements were repeated three times. The experimental solubility of barnidipine fraction (X2) in each solvent was calculated using Equation 5. The relative deviations (RD) between the experimental data and the literature data were less than 3%, which indicates that the measurement system and method used were reliable and accurate.
In the formula,M1 andM2 are the relativemolar massof barnidipine and solvent, respectively, and m1 is the mass of solute and m2 represent the mass of pure solvent.
Results
Solid-state properties of barnidipine
Differential scanning calorimetry was performed for the original powder and for the solid phase after equilibration with the pure solvents, this allows to detect possible changes of the thermal properties of the solid phase. The DSC thermogram of barnidipine is depicted in Figure 2. The thermal analysis results showed that the onset temperature and specific fusion enthalpy (ΔHF ) were 230 °C and 75.6 J/g respectively, associated with the polymorphic form II. The use of form II provides a new opportunity to improve and facilitate the handling and storage of barnidipine hydrochloride since it is a light-stable crystalline form. Characterization of the original barnidipine powder solid phase and the equilibrated solid phases with the selected pure solvents showed in all cases the same melting-related endothermic event, suggesting that barnidipine exists in a pure crystalline form that was not transformed into no polymorphic form after solubility experiments performed. Unfortunately, there is not much information previously published in relation to the barnidipine polymorphism, a patent approved in 2014 has been found, on polymorph of barnidipine hydrochloride and processes for its preparation.23
Experimental solubility data of barnidipine in seventeen mono solvents
The experimental mole fraction solubility data of barnidipine in seventeen mono solvents at 298.15 K and the partial parameters and total solubility parameters of solvents chosen are tabulated in Table 2. It can be seen temperature has different effects on the solubility change trend of various types of solvents24. Experimental mole fraction solubility was ranked in the following order: isopropyl myristate < benzene < chlorobenzene < ethyl acetate < water < 1,4-Dioxane < acetone < acetonitrile < 1,2-Dichloroethane < 1-Octanol < 1-Pentanol < ethanol < acetophenone < methanol < DEGME < acetic acid < DMF. As can be appreciated, the solubility of barnidipine increases to a maximum with solvents as DEGME, acetic acid or DMF, are Lewis-acid solvents suggesting that barnidipine is a better proton-acceptor than proton-donor. According to this result, solubility of barnidipine is completely analogous to the order of polarity, this result may be due to the higher polarity of barnidipine. Solvents like DMF or acetic acid, contain similar groups of C=O than the drug, which may lead the larger solubility. In addition, the intermolecular interactions such as hydrogen bonds and Van der Waals’ forces between solvent-solvent and solute-solvent will also influence the solubility. Then the solubility data would be helpful in separation, purification studies and formulation development of barnidipine in chemical and pharmaceutical industries.
Table 2. Values of HSP of selected solvents and equilibrium solubility of barnidipine in mole fraction scale in pure solvents at T/K = 298.15.
| Solvents | δd | δp | δh | δT | X2 | Δδ | Weight |
|---|---|---|---|---|---|---|---|
| Ethanol | 15.8 | 8.8 | 19.4 | 26.5 | 1.87·10-4 | 7.36 | 0.01 |
| Water | 15.6 | 16 | 42.3 | 47.9 | 1.42·10-5 | 20.79 | 1 |
| Ethyl acetate | 15.1 | 5.3 | 9.2 | 18.5 | 7.82·10-6 | 16.15 | 0.01 |
| 1,4-Dioxane | 19.0 | 1.8 | 7.4 | 20.5 | 2.35·10-5 | 20.37 | 1 |
| Acetic acid | 14.5 | 8.’ | 13.5 | 21.4 | 4.32·10-3 | 11.13 | 0.01 |
| 1-Pentanol | 13.0 | 4.5 | 13.9 | 21.7 | 1.06·10-4 | 13.61 | 1 |
| DMF | 17.4 | 13.7 | 11.3 | 24.8 | 6.67·10-3 | 10.88 | 0.01 |
| Benzene | 18.4 | 1 | 2 | 18.6 | 5.56·10-7 | 24.79 | 1 |
| Cl-Benzene | 19.0 | 4.3 | 2 | 19.6 | 1.27·10-6 | 23.1 | 0.01 |
| 1-Octanol | 17.0 | 3.3 | 11.9 | 20.9 | 9.75·10-5 | 15.93 | 1 |
| Acetophenone | 19.6 | 8.6 | 3.7 | 21.7 | 3.61·10-4 | 19.91 | 1 |
| Acetone | 15.5 | 10.4 | 7 | 20 | 6.17·10-5 | 15.52 | 1 |
| Isopropyl myristate | 15.9 | 2.1 | 2.8 | 16.3 | 5.02·10-7 | 23.21 | 1 |
| DEGME | 15.5 | 5.7 | 11.2 | 19.95 | 6.00·10-4 | 14.43 | 0.01 |
| Methanol | 15.1 | 12.3 | 22.3 | 29.6 | 5.33·10-4 | 3.55 | 1 |
| Acetonitrile | 15.3 | 18 | 6.1 | 24.4 | 7.67·10-5 | 15.65 | 1 |
| 1,2-Dichloroethane | 19.0 | 7.4 | 4.1 | 20.8 | 7.67·10-5 | 19.87 | 1 |
The solvents with a less ability for solubilizing barnidipine (isopropyl myristate, benzene and chlorobenzene) have small total solubility parameters. The solubility in primary alcohols, 1-Octanol, 1-Pentanol, ethanol, and methanol also follows the order of increasing solubility parameter. With the decrease of the carbon chain length, the solubility of barnidipine increased significantly, and the maximum values were obtained in methanol. Overall, explaining the dissolution behavior of barnidipine requires the consideration of solid-liquid equilibrium is affected by different interactions. So barnidipine is easier to dissolve in solvents with shorter carbon chains and higher polarity.
On the other hand, the effect of mole fraction on Δδ, key parameter to judge the ability of solvent to dissolve solute (eq. 3), was evaluated and the results are included in Fig. 3. To facilitate the interpretation of the results, a number has been assigned to each solvent (Table 2). Ethanol and methanol are the solvents that are furthest away. Δδ were found to decrease linearly with increasing molar fraction. The maximum solubilization of barnidipine could be possible due to upper polarity and different solute-solvent interactions. Accordingly, DMF could be utilized as an efficient cosolvent in the solubilisation process.
An approximation to the calculation of the cohesive energy and the solubility parameter of drug were made from group contribution methods. Table 3 summarizes the results of the application of the group contribution method of Fedors25 for estimate interne energy (ΔE), molar volume (ΔV), and total Hansen solubility parameter of barnidipine δ2 = 23.2 MPa1/2. According to the group contribution method proposed by Hoftyzer-Van Krevelen δd, δp, δh and δT of barnidipine can be calculated, as can see in Table 4.
Table 3. Application of the group contribution method of Fedors25 for estimate interne energy, molar volume and total Hansen solubility parameter of barnidipine.
| Group or atom | ni | ΔEi(kJ/mol) | ΔVi(cm3/mol) | niΔEi (kJ/mol) | niVi (cm3/mol) |
|---|---|---|---|---|---|
| (-CH3) | 3 | 4.71 | 33.5 | 14.13 | 100.5 |
| (-CH2-) | 4 | 4.94 | 16.1 | 19.76 | 64.4 |
| (>CH-) | 2 | 3.43 | -1 | 6.86 | -2.0 |
| (>C=) | 4 | 4.31 | -5.5 | 17.24 | -22.0 |
| Phenyl | 1 | 31.90 | 71.4 | 31.90 | 71.4 |
| Phenylene | 1 | 31.90 | 52.4 | 31.90 | 52.4 |
| Ring closure-5 | 2 | 1.05 | 16.0 | 2.10 | 32.0 |
| Conj in ring | 2 | 1.67 | -2.2 | 3.34 | -4.4 |
| (-COO-) | 2 | 18.00 | 18.0 | 36.00 | 36.0 |
| (-NH-) | 1 | 8.40 | 4.5 | 8.40 | 4.5 |
| (-N<) | 1 | 4.20 | -9.0 | 4.20 | -9.0 |
| (-NO2) arom | 1 | 15.36 | 32.0 | 15.36 | 32.0 |
| 191.19 | 355.8 | ||||
| δ2 = (∑ni Ei /∑ni Vi )1/2 = 23.2 MPa½ =11.34 (cal/cm3)½ | |||||
Conversion of (J/cm3)1/2 or MPa1/2 into (cal/cm3)1/2 is simple because it only requires division by 2.045.
Solvent effects: KAT-LSER model
The KAT-LSER (Kamlet-Abboud-Taft linear solvation energy relationship) model is applied to the barnidipine solubility to explain the Lewis-acid-base and polarization effects upon improvement of this property. Classical KAT-LSER model takes the form of Equation 6.26,27
where,c1 α and c2 β refer to the energy terms for specific solute-solvent Lewis acid and base interactions, respectively; c3 π represents the energy term for non-specific interactions; whereas, the last term in the Equation 6 denotes cavity term defining the energy for solvent-solvent molecule interactions. This term designates the drug accommodation energy as a product of the Hansen solubility parameter, δ1, and molar volume of barnidipine,V2 . The universal gas constant,R, and experimental temperature,T/K, are considered here in denominator with the purpose of getting a dimensionless magnitude of the cavity term.c0 represents the solute-solute interactions and measures the intercept at α = β =π= δ2 = 0;c1 andc2 are a measure of the property susceptibility of barnidipine to solute-solvent interactions of specific hydrogen bonding, whilec3 andc4 represent the solute sensitivity to the nonspecific electrostatic solute-solvent and solvent-solvent molecule interactions.
Table 5 summarizes the solvatochromic parameters,α, β, and π, as well as the Hansen solubility parameters of 15 solvents studied in this research taken from the literature.28-32
Table 5. Solvatochromic parameters and total Hansen solubility parameter of some solvent studied.
| Solvent | αa | βa | πa | δ2 (MPa1/2)b |
|---|---|---|---|---|
| Ethanol | 0.86 | 0.75 | 0.54 | 26.5 |
| Water | 1.17 | 0.47 | 1.09 | 47.8 |
| Ethyl acetate | 0.00 | 0.45 | 0.45 | 18.1 |
| 1,4-Dioxane | 0.00 | 0.37 | 0.49 | 20.5 |
| Acetic acid | 1.12 | 0.45 | 0.64 | 21.4 |
| 1-Pentanol | 0.84 | 0.86 | 0.40 | 21.7 |
| DMF | 0.00 | 0.69 | 0.88 | 24.8 |
| Benzene | 0.00 | 0.10 | 0.55 | 18.8 |
| Cl-Benzene | 0.00 | 0.07 | 0.68 | 19.8 |
| 1-Octanol | 0.77 | 0.81 | 0.40 | 21.0 |
| Acetophenone | 0.04 | 0.49 | 0.81 | 21.8 |
| Acetone | 0.08 | 0.48 | 0.62 | 20.0 |
| Methanol | 0.98 | 0.66 | 0.60 | 29.6 |
| Acetonitrile | 0.19 | 0.40 | 0.66 | 24.4 |
| 1,2-Dichloroethane | 0.00 | 0.10 | 0.73 | 20.9 |
aTaken from Marcus.(33)
bTaken from Barton.(20)
In this way, KAT-LSER model obtained is shown as Equation 6 (with r = 0.905 and F = 11.36).
Positive values of c1 (3.24), c2 (7.14) and c3 (15.80) demonstrate the favourable contribution of Lewis-acid base and polarizability of barnidipine solubility, whereas the negative values of c0 (-20.28) and c4 (-4.55) demonstrate the unfavourable contribution of solute-solute interactions and cavity energy requirements on the solubility of this drug. Moreover, if absolute values of c1, c2, c3 and c4 are compared the following contribution percentages are obtained: 10.6, 23.2, 51.4 and 14.8%, respectively, which means that polarization effects implies the higher contribution on solubilisation, followed by the Lewis basic behaviour of barnidipine owing tertiary amine group and oxygen atoms, whereas the Lewis acidic behaviour of this drug is the lowest favourable contributor and it could be due to hydrogen atom of secondary amine group.
Discussion
Hansen solubility parameters
Robust regression methods as well as analysis of residuals were used to detect inconsistencies of individual cases with the overall regression model. From these results, weighted regression were performed to obtain the partial solubility parameters, i.e. smaller weights were assigned to the solvents that least fitted the models. The parameters are calculated from regression coefficients that are statistically significant at least at the 0.05 probability level using Eq. 4.17,18 using the dependent variable, lnX2. A weight of 0.01 was assigned to the following solvents: ethanol, ethyl acetate, acetic acid, chlorobenzene, DEGME and DMF which least fit the model. For the remaining solvents the weight was fixed at unity.
The results of partial solubility parameters for barnidipine from experimental values are δd =14.32 MPa1/2; δp =15.69 MPa1/2; δh =21.55 MPa1/2 and for total solubility parameter is δT =30.25 MPa1/2, that experimental value is not close to obtained using Fedors or Hoftyzer-Van Krevelen methods. This indicates that the actual polarity of the drug against the solvents is larger than expected from the additive contribution of its groups. On the other hand, the experimental δT obtained is in excellent agreement with the value calculated from the Fedors method. The reason may be that the Fedors method includes a larger number of groups than the Hoftyzer-Van Krevelen method. The group contribution methods are useful because they provide a rough estimation of total and the partial solubility parameters.
Δδ factor has been well established in the literature that the smaller the difference in solubility of two compounds is the more miscible they are Hoftyzer-Van Krevelen method is of the same order of accuracy and the optimal way for estimation of the solubility parameter is to apply both taking the average results Table 2 summarizes the values obtained, as can see methanol and ethanol are the two best solvents for barnidipine, representing the smallest increment values, that is, solubility depends on hydrogen bonding (δh ) preferentially. To describe the miscibility between barnidipine and the pure solvents, Δδmethanol =3.55, parameter appointed for mutually miscible systems. It can be concluded that when the parameters of barnidipine are closer to those of the selected solvent, barnidipine will theoretically be more soluble in the solvent. This indicates that the difference values (Δδ) are important indexes to predict the extent of dissolution.
Conclusion
ln X2 as dependent variable was used, r2 value is higher (>0.98) and all the regression coefficients are significant. The total and partial solubility parameters obtained are in quite good agreement considering the structure of the drug, δ T =30.25 MPa1/2.
Barnidipine is easier to dissolve in solvents with shorter carbon chains and higher polarity. The influence of solute-solvent interaction, solvent-solvent interaction, physical and chemical properties of solute and solvents were studied and analysed.
Experimental data were compared with the data calculated according to the Fedors and Hoftyzer-Van Krevelen methods to show the importance of using both methods to determine HSP. It is interesting to evaluate the experimental and theoretical values estimated from the group contribution methods of Fedors for total solubility parameters and Hoftyzer-Van Krevelen for total and partial solubility parameters.
According to KAT-LSER model, solvent effect (solvent interaction) was investigated through correlating barnidipine solubility data in selected solvents. It turns out that the self-cohesive interaction of the solvent may have a more significant weight on the solubility of barnidipine.