INTRODUCTION

The worldwide prevalence of overweight and obesity has increased remarkably over the past decades ^1,2, which is associated with attempting to lose weight. Nowadays, there are different dietary strategies to slimming and many of these lead to an initial weight loss from 5 to 9%, which seems stable over the first six months. In most cases, in fact, the real problem lies not in weight loss, but in the maintenance of long-term weight reached: a meta-analysis study on the body weight reduction showed that after 48 months half of the body weight lost is regained ³. In addition, the National Health and Nutrition Examination Survey (NHANES) has shown that 35% of people who have achieved a significant reduction in weight have regained it after one year. Even today it is believed that the principle which underpins the process concerning the change in body weight resides in the balance between the energy content of food eaten and the energy expended by the body to maintain vital functions and associated with physical exercise relationship ⁴. Since living organisms obey to the first principle of thermodynamics, the energy balance equation is used to predict changes in body weight as a result of a variation in energy intake or/and in energy expenditure. Despite the simplicity of this principle, the calculation of the energy balance change and the translation of this one in a change in body weight is not simple. Often, the static equation of energy balance is used improperly; in fact, energy intake is equal to energy expenditure only in a particular case: when body weight and body composition are maintained constant ⁵. It is not considered that the process is dynamic and that the variation of energy expenditure depends itself on the variation of body mass, due both to an increase and to a decrease of weight ^6,7,8. The "rule of body weight loss" is derived from the estimation of the energy content of the lost weight, but ignores the dynamic physiological adaptations that arise during the change of weight, which lead to changes both in the basal metabolic rate and in energy expenditure for physical activity ⁹. Unfortunately, this static rule for weight loss continues to be used in prescriptions and advice geared to slimming, and at the population level it is applied to predict the effect on the prevalence of obesity and the effect of certain programs ^10,11,12,13. These same concerns, together with the numerous contradictions emerged from a proportional and linear conception of the masses changing processes, as well as the use of static energy balance equation for predicting the resulting changes in body mass, contributed to design a new method abbreviated as BFMNU (Biologia e Fisiologia Modellistica della Nutrizione Umana) ^14,15), according to which it was possible to predict the change in mass and body composition in response to a change in mass and food energy introduced.

The aim of the study was to evaluate the relationship between the energy contained in food from the diet (energy supply) and body mass, on a large and heterogeneous sample of 120 subjects in various pathophysiological conditions. In addition, other correlations were analyzed: between food energy and food mass, and between the ∆% of body mass and the ∆% energy food supplied after the elaboration of the diet.

METHODS

The study concerns the collection, from the database, of the data of 120 subjects in a variety of pathophysiological conditions, which had previously been followed in a dietetic path of annual duration (BFMNU method), for which all the information necessary for the research was available.

The BFMNU method was devised by Pietro Marco Boselli ¹⁸ in 1995 with the objective of proposing a new nutritional intervention method, different from the existing ones, which was able to systemically interpret the metabolic processes of mass and energy, and to overcome the many and obvious contradictions of the methods already in use. It is a phenomenologic-mathematical method applicable to any individual, at any physiopathological condition, whose primary objective is to determine the optimal diet that most of all is capable of producing a synergistic change in body mass, body composition and energy in order to improve the functionality of the body with the smallest possible variation in comparison to previous eating habits. In order to achieve this goal, and therefore provide an adequate diet, it is necessary to know the starting body composition: the method uses the measurement of lengths and circumferences to calculate volume (V), the surface area (S) and pseudo thickness (Sp), considering the body as a set of geometric solids; through these structural variables the body composition can be calculated as follows ¹⁴:

In this formulae, Mw , Mp , Ml , Mg and Mt are respectively the body masses of water, proteins, lipids, carbohydrates and total, expressed in kg , S is the body surface area in m2, V is the volume expressed in dm3 and Sp is the pseudo thickness in cm. Through the use of the DIES4 software, specifically designed for the application of the BFMNU model and the facilitation of calculations, the constant rates related to each component can be determined:

For this study, 120 subjects including men, women and children, aged 7 to 78 years, were randomly selected from a pool of subjects who followed the BFMNU diet for a period of one year, in years 2010-2015. For each subject data were collected, including age, body mass (Mc), initial body mass index (Mci) and the final body mass (Mcf) corresponding to stable weight reached, the height (h) and the body mass index (BMI). There were also collected data about the diet normally followed before the BFMNU dietetic treatment, resulting from food consumption diaries filled in by them, such as food mass (Ma) and the daily food energy (Ea). The food consumption data were obtained using the protocol provided by the BFMNU method: this involves the compilation by the subject of a diary of nutrition and excretion in which the subject for three days, including two weekdays and one during the weekend (not necessarily consecutive), must note the weight (g) of each food and/or drink consumed and the weight of urine and feces excreted. The diary must adhere to the representativeness and accuracy requirements, for which the individual must follow to write what normally is part of his current diet, and that has been part over a period of at least eight months prior to the compilation. The study was approved by the Ethical Committee of University of Milan (Italy).

RESULTS AND DISCUSSION

The correlation between MCi of the subjects and Ea introduced was investigated, corresponding to the diet followed by the person before the dietetic treatment. The correlation index amounted to 12.5% and therefore, it is insufficient to justify a valid linear correlation between the two variables mentioned (Fig. 1). As shown in figure 1, the points on the graph, each representing a different subject, are randomly distributed and the regression applied is actually meaningless; it just puts in evidence the great dispersion of experimental points.

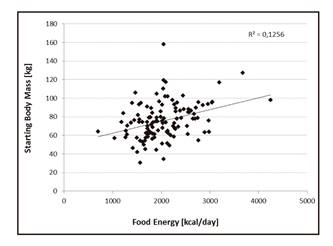
Figure 1 Correlation between food energy (Ea) characteristic of the subjects' habitual diet subjects and starting body mass (MCi). 

Figure 2 shows the distribution of the starting body mass (MCi) and the food energy normalized on starting body mass (Ea/MCi), whose correlation is equal to 29.2%. Despite being increased compared to that shown in figure 1, the correlation index is still insignificant: dietary energy justifies body mass only for a quarter of the subjects considered. Additionally, this distribution highlights another aspect: the basal metabolic rate changes with the body mass so greater than the extra basal metabolism, because it is connected to the evaporation rate (perspiratio insensibilis) and then to the body surface. Therefore, the increase of the index value of correlation shown in figure 2 is a consequence of the operation of normalization: the body mass is in fact more correlated with the ratio Ea/ MCi than with Ea.

Based on the results obtained, is it possible to change the body mass of an individual by changing the intake of food energy? Is it possible to predict changes in body composition by relying on the static equation of energy balance?

Figure 2 Correlation between food energy (Ea) normalized on starting body mass (MCi) and starting body mass. 

The fact that emerges, that is that there is no significant correlation between Ea and MCi, questions the validity of all diets determined on an energy basis.

Actually, what correlates body mass with food mass (and also body energy with food energy) is the metabolism of the subject, characterized by the metabolic constant rates (k) that are specific of the individual himself. In fact, the metabolic rates explain how the outcome of body mass can be independent of the food energy introduced with the diet ¹⁵.

The correlation between food mass (Ma) and food energy (Ea) was also studied (Fig. 3) and, contrary to what might be expected, the correlation coefficient is equal to 0.211: with the same amount of food mass, the energy content varies depending on the composition of nutrition.

Figure 3 Correlation between food energy (Ea) and food mass (Ma). 

Finally, on the set of the collected data, we studied the relationship:

The correlation is highly significant and shows that about 96% of the percentage changes of dietary energy justify the percentage change in body mass (Fig. 4). It should be considered that the percentage changes, both of the body mass and food energy, are dimensionless and without units of measurement. Therefore, the non-rectilinear correlation found only expresses the link between the numerical values: this, however, allows to predict the final body mass (Mcf) of the subject after the variation of food energy (Ea) caused by the new diet obtained through the solution of the system of metabolic balance.

Figure 4 Correlation between percentage changes of body mass and percentage changes of food energy. 

The same correlation, applied to the food energy data suggested by diets formulated on an energy basis, produces a correlation index R2 = 0.3439. This result shows the difference between the two different approaches, BFMNU and diets on an energy basis, and especially the inadequacy of the latter.

The results concerning the non-correlation between Ea and Mci emerged in our study reflect and confirm the doubt which motivated the initial choice to perform this type of analysis. As shown by Alpert ¹⁶, the commonly used energy balance equation is inadequate to predict changes in body mass consequent to different energy supplies. In addition, small increases in taking energy during long periods cannot lead to higher weight gains, as often claimed ^16,17. The only exception is within the same individual under equilibrium conditions: with the same diet, metabolism, and pathophysiological conditions, in the same individual, the correlation between Ea and Mc is still valid, as motivated by the specific heat of macronutrients. Instead, the correlation between Ea and Mc, applied in situations of imbalance, that is, in most cases, is not significant from the biological point of view; for this reason, it is necessary to consider the calculation of quantitative balances (mass - mass and energy - energy). It is therefore necessary to update the existing standard by which nutrition plans are prescribed for any changing and stabilization of body weight and statistical evaluations are made on the population scale. Being able to customize nutrition on the individual, on the basis of its metabolic speed, allows minimizing the experimental errors due to inference of the energy expenditure of the subject, as well as the maximization of the result on the progress and improvement of body composition ¹⁸.