INTRODUCCIÓN
El empleo de gases de uso aeronáutico es de enorme importancia para las unidades aéreas. Los parámetros analíticos del oxígeno de alta cota (líquido y gaseoso) están determinados por el STANAG 7106 y es el personal farmacéutico militar de los Centros de Farmacia del Aire los que efectúan, garantizan e interpretan los análisis. Desde el año 1997 se han realizado expedientes de contratación para el suministro de oxígeno de vuelo, otros gases y elementos asociados para el Ejército del Aire y el Centro de Farmacia del Aire de Madrid (CEFARMA) ha sido el responsable de los mismos. El ahorro económico por la centralización del suministro del material y productos se han considerado muy aceptables por el Mando Logístico del Aire (MALOG). No obstante, desde el 2007 se han producido desajustes entre lo programado como gasto y lo realmente ejecutado como tal. Esto ha llevado, en ocasiones, a que el CEFARMA solicite la devolución de asignaciones económicas o requiera nuevos créditos presupuestarios para hacer frente al consumo y servicios efectuados por las empresas. Así, en el año 2011 se solicitó una reducción del 17 % sobre el total del expediente (50% de la asignación económica anual). En el año 2014 se efectuó la devolución de más de la cuarta parte de la prorroga asignada para gasto en oxígeno de alta cota y en los años 2015 y 2016 también se produjo el reintegro anual del 18% del total del expediente. Por otra parte, en los años 2009 y 2010 se efectuaron ampliaciones y prorrogas de contrato por un importe total de casi un millón de euros para hacer frente a suministros no inicialmente estimados. Por ello, es importante realizar previsiones económicas, lo más ajustadas posibles, para evitar singularidades presupuestarias en las partidas referentes al oxígeno de alta cota y elementos afines. El objetivo de este trabajo es realizar estimaciones econométricas1, a partir de las series temporales de consumo, para efectuar adecuadas previsiones de gasto agregado en futuros expedientes de contratación referidos al suministro de oxígeno de vuelo, otros gases y elementos asociados utilizados en el Ejército del Aire.
El objeto del análisis de una serie temporal es el conocimiento de un patrón de comportamiento para prever una acción futura (siempre que las condiciones sean estables), ya que son un conjunto de observaciones ordenadas en el tiempo que muestran la evolución de un fenómeno o variable a lo largo de él1,2. Lo habitual es identificar cuatro componentes que son: tendencia, estacionalidad, ciclos y residuos. El orden en el que se producen los fenómenos o variables a estudiar es esencial y modificarlo implica alterar la información que existe en la serie. Cualquier serie temporal se forma por un conjunto de observaciones de una variable dependiente tomadas durante un tiempo, que tienen dos importantes elementos: uno de carácter determinista y que permanece en el tiempo y otro aleatorio que es lo que se conoce como error o ruido blanco del proceso2,3.
Es importante destacar que, si al conocer la evolución de la serie en el pasado se pudiese predecir exactamente el comportamiento futuro, estaríamos ante un comportamiento totalmente determinista cuyo estudio no comportaría interés al estar formulado por leyes matemáticas y físicas, bien conocidas. En general, las series temporales están asociadas a fenómenos aleatorios y su estudio permite acercarse a su estructura para realizar pronóstico futuro1,3.
Los parámetros estadísticos no temporales se han criticado por sus limitaciones e invalidez cuando hay correlaciones entre los términos de error. Por ello, se han propuesto diferentes soluciones con el objeto de eliminar los problemas de autocorrelación2 en las series temporales. En la actualidad, entre las más empleadas, está la técnica de modelado conocida por su acrónimo ingles ARIMA (autorregresivo integrado de media móviles)2. Fue desarrollado por Box, Jenkings4 y Tiao5 y resulta un método muy útil para tratar tendencia, estacionalidad y error aleatorio de las series temporales.
MÉTODO
Procedimiento Box-Jenkings
Según este método, cada observación, en un momento determinado, es modelada en función de los valores anteriores. Es un enfoque basado en determinar el modelo probabilístico que rige el comportamiento de la serie temporal. La metodología por este sistema se fundamenta en realizar una identificación del patrón, estimación de parámetros y diagnosis del modelo3,6,7.
Los modelos se conocen con el nombre genérico de método “autorregresivo integrado de medias móviles”, ARIMA (AutoRegresive Integrated Moving Average), que deriva de sus tres componentes: AR (autorregresivo), I (integrado) y MA (Medias Móviles).
Un modelo se define como autorregresivo si la variable interna de un periodo determinado es posible explicarla por las observaciones, de ella misma, de los periodos anteriores (de su propio pasado), añadiéndose, además, un término de error. Si el proceso es estacionario y presenta una distribución normal, en determinadas condiciones previas, toda variable Yt se puede expresar como una combinación lineal de sus valores pasados y de un componente de error6.
El modelo general ARIMA (p,d,q) se denomina proceso autorregresivo integrado de medias móviles de orden p, d, q y toma la expresión general de la siguiente ecuación:
(1-a1L1-a2L2-…….-apLp)(1-L)dYt=(1-b1L1-b2L2-…….bqLq)Ԑt
Siendo:
Yt: valor de la variable en el momento t.
L: operador de retardos (Yt-1=Yt*L).
ap: coeficientes del operador de retardos para el componente autorregresivo.
bq: coeficientes del operador de retardos para el componente de medias móviles.
Ԑt: componente aleatoria.
El término de error se denomina ruido blanco y tiene que ser de media nula, varianza constante y covarianza nula entre errores de observaciones diferentes7.
Un modelo ARIMA (0, d, 0) es una serie temporal que se convierte en ruido blanco después de ser diferenciada d veces. Los modelos ARIMA (p, d, q) permiten describir las observaciones tras haber sido diferenciadas d veces para eliminar las posibles fuentes de no estabilidad. Si hay un componente igual a cero o es nulo se excluye del término correspondiente de la fórmula general7.
Sin entrar en detalles, para que un proceso aleatorio tenga una formulación de tipo ARIMA es necesario que se cumpla la condición de estabilidad. En la práctica la serie temporal ha de ser, al menos, débilmente estacionaria. Si se quiere determinar la estructura del proceso estocástico mediante un modelo de tipo autorregresivo es necesario asegurarse que la serie es estacionaria, y si no lo es, hay que transformar la serie temporal original para obtener otra serie temporal que cumpla el criterio de invariabilidad con respecto al tiempo6,8.
La verificación de la constancia temporal de la serie, en media, se puede realizar de diferentes maneras. Normalmente, el gráfico permite determinar fácilmente si existe tendencia o es estable durante periodos temporales determinados5,6. Si hay tendencia, se trabaja sobre los residuos o se diferencia la serie para hacerla estacionaria (estacionaria en varianza). Para determinar que la serie temporal presenta invariabilidad temporal en varianza (orden de integración) se realiza el llamado test de Dickey-Fuller Ampliado (test DFA)6. En este test la hipótesis nula es la ausencia de invariancia en el tiempo (si el valor estimado es menor, en valor absoluto, que el tabulado, dentro de un determinado nivel de confianza, se admite la hipótesis nula: ausencia de invariancia temporal, o lo que es lo mismo “presencia de una raíz unitaria”). Si se acepta la hipótesis nula, la serie no es útil para el modelo ARIMA.
Existen otros modelos de análisis de series temporales no autorregresivos igualmente válidos para realizar predicción en este contexto. Entre ellos destacan el análisis de suavizado exponencial, aditivo o multiplicativo, lo basados en transformadas de Fourier o incluso los realizados a partir de análisis de recurrencia, simulaciones de Montecarlo y redes neuronales. La matemática necesaria y el software para desarrollarlos no es fácil de aplicar, aunque las conclusiones finales son semejantes a las obtenidas a partir de los procesos autorregresivos. Los modelos ARIMA son muy útiles porque su empleo se fundamenta en modelos de carácter estacionario que en la práctica son muy apropiados para estudiar la vinculación retrospectiva de los valores de una serie temporal. Un estudio general de la metodología de procesos autorregresivos supone su extensión tanto a modelos aditivos como a modelos multiplicativos. En este trabajo se ha utilizado el modelo aditivo en el que cada dato tiene una dependencia lineal de los valores de su pasado.
MATERIALES
Se han recopilado todos los datos económicos de las unidades aéreas que están integradas o han solicitado su incorporación a los diferentes expedientes para el suministro de gases desde el año 2004 hasta el año 2017. Los datos se han obtenido de los certificados de facturación, facturas y albaranes en los que se detallan el consumo e importe, la fecha de facturación y la unidad a la que pertenece la misma.
Los importes se han deflactado3 tomando como año base el 2016 y, posteriormente, se han agrupado por meses, trimestres y años.
La agregación de datos se ha realizado con la aplicación Filemaker Pro Advanced V15 (©Filemaker inc,). Para el tratamiento estadístico y econométrico se han utilizado los programas informáticos Microsoft® Excel (2016), Eviews® 10.0 (IHS inc.), Gretl (2017c) y Statistica v 12 (StatSoft, 2014).
RESULTADOS
Se han estudiado las series temporales correspondientes al número de facturas y al gasto total trimestral agregado facturado entre los años 2004 y 2018.
En la figura 1 se muestran las series temporales de gasto trimestral agregado para todas las unidades aéreas (en términos constantes, deflactadas) y número de facturas pagadas para los expedientes de suministro de oxígeno y elementos asociados desde el año 2004 al año 2016.

Fuente: elaboración propia.
Figura 1 Evolución de gasto trimestral (en términos constantes) y número de facturas pagadas para los expedientes de suministro de oxígeno y elementos asociados desde el año 2004 al año 2016.
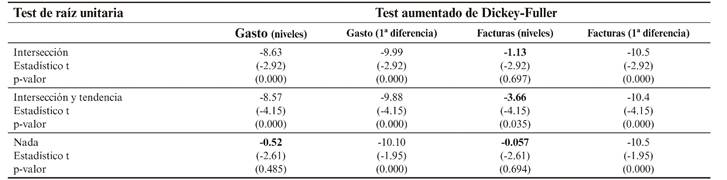
En la tabla 1 se exponen los resultados del test de raíz unitaria realizado con el estadístico aumentado de Dickey-Fuller (test ADF). A partir de los gráficos de la figura 1 puede deducirse que la serie temporal que se corresponde con el gasto trimestral podría llegar a considerarse estacionaria. El test ADF permite identificar la existencia de raíces unitarias. Se observa, en la tabla 1, que para las series temporales gasto y facturas, en niveles, existe ausencia de constancia en el tiempo. En necesario rechazar la hipótesis de ausencia de invariabilidad temporal para los niveles (datos reales) y aceptar que es estacionaria en primeras diferencias. Por ello, ambas series son integradas de orden 1. Existen otros contrastes de hipótesis que pueden ser utilizadas como comparación. Entre ellos destaca el contraste de Phillips-Perron (PP) que conduce a resultados y conclusiones semejantes a las del test ADF7.
Tabla 1 Resultados del test de raíz unitaria realizado con el estadístico aumentado de Dickey-Fuller para demostrar la estabilidad de las series diferenciadas (los resultados en negrita indican ausencia de estabilidad). Software utilizado: Eviews® 10. Fuente: elaboración propia.
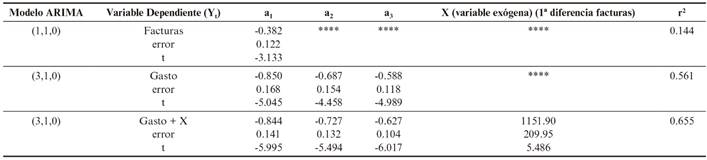
En la tabla 2 se detallan los resultados calculados para los coeficientes del componente autorregresivo de cada modelo ARIMA estudiado, con indicación del error estándar y el valor de significatividad del estadístico t-Student. Las series temporales son integradas de primer orden. Las series no estacionarias que presentan una tendencia lineal, normalmente, se transforman para convertirlas en estacionarias utilizando la ecuación Et=Xt-Xt-1. La primera diferencia de esta nueva serie no tendrá tendencia y Xt es, entonces, una serie temporal, homogénea, integrada de orden uno7. Si la tendencia es cuadrática se realiza la diferenciación en dos etapas, en primer lugar, Ft=Xt-Xt-1 y posteriormente Et=Ft-Ft-1. La serie Xt será homogénea e integrada de orden 2 (segundo orden). Lógicamente, para tendencias de orden p, será necesario realizar p diferenciaciones y las series se conocerán como integradas de orden p. En las series temporales que existe una tendencia de tipo exponencial esta puede eliminarse calculando, inicialmente, el logaritmo y después la primera diferencia de la serie logarítmica (Et=lnXt-lnXt-1)6,7,9.
Tabla 2 Valores de los coeficientes del componente autorregresivo para los modelos ARIMA estudiados. Se ha indicado el valor del coeficiente de determinación (r2) encontrado en cada modelo autorregresivo, así como los resultados obtenidos para el error estándar y t-Student. Software utilizado. Gretl (2017 c) y Eviews® 10. Fuente: elaboración propia.
En la tabla 3 se recogen las ecuaciones finales obtenidas para realizar el cálculo predictivo en el gasto agregado trimestral total para los expedientes de gases. El pronóstico del gasto agregado anual se obtiene de la suma trimestral utilizando cada una de las ecuaciones propuestas, de forma independiente. Para el modelo ARIMA (3,1,0) con variable exógena, X, esta ha sido el número de facturas. La serie temporal X: número de facturas se corresponde con la factura por cada servicio de suministro realizado y puede estimarse, trimestralmente, a partir del modelo ARIMA (1,1,0).
Tabla 3 Ecuaciones de pronóstico de gasto trimestral conjunto y número de facturas relacionadas con el gasto trimestral agregado para los expedientes de gases. Las ecuaciones han sido adecuadas para realizar prospectiva de gasto para el año 2017. Una vez concluido el ciclo anual será necesario recalcular los coeficientes para obtener nuevas ecuaciones de predicción de gasto conjunto y ser utilizadas para el año 2018. Software utilizado. Gretl (2017 c) y Eviews® 10. Fuente: elaboración propia.
| Variable dependiente | Modelo ARIMA | Ecuación propuesta |
|---|---|---|
| Nº Facturas (Yt) | (1,1,0) | 0.618*Yt-1+0.382*Yt-2 |
| Gasto trimestral (Yt) | (3,1,0) | Yt = 0.150*Y t-1+0.163*Y t-2+0.099*Y t-3+0.588*Y t-4 |
| Gasto trimestral (Yt) | (3,1,0) | Yt =0.156*Y t-1+0.117*Y t-2+0.100*Y t-3+0.627*Y t-4+ +1151.90*Xt -179.70*Xt-1 -134.86 *Xt-2115.10*Xt-3-722.24*Xt-4 |
(X: nº de facturas)
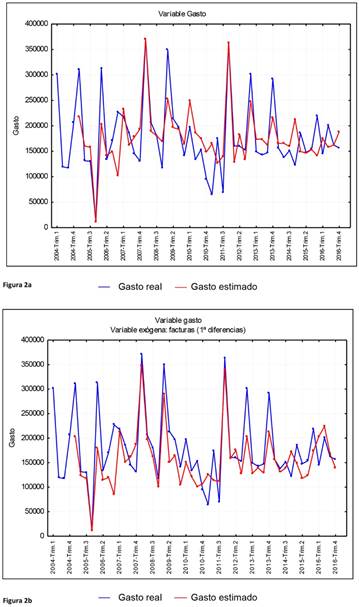
En la figura 2 se muestra el grafico de gasto trimestral real y gasto trimestral calculado y pronosticado partir de la ecuación del modelo ARIMA (3,1,0) sin variable exógena y con variable exógena (X: número de facturas) para el periodo de tiempo 2004-2016. Las ecuaciones de los modelos autorregresivos se extienden para la totalidad del año 2017 y permiten explicar entre el 55 % y 65 % de la posible variabilidad que se pueda dar en el gasto total para todas las unidades aéreas incorporadas a los expedientes de gases (figura 3).
Fuente: elaboración propia.
Figuras 2ay 2b Gráfico de gasto agregado trimestral real y gasto agregado trimestral estimado a partir de la ecuación de los modelos ARIMA (3,1,0) con ausencia (a) y presencia (b) de variable exógena (X: número de facturas). Las líneas de color azul son los datos reales y las de color rojo se corresponden con los datos estimados El gasto se da en euros constantes. Software utilizado Statistica v 12 y Eviews® 10.

Fuente: elaboración propia.
Figuras 3a y 3b Gráficos de regresión lineal de datos reales frente a estimados para los modelos ARIMA (3,1,0). Dependiendo del modelo utilizado, ausencia (3a) o presencia de variable exógena (3b), la variabilidad total explicada por las ecuaciones oscila entre el 55% y el 65% de la totalidad de incertidumbre presente. El gasto se da en euros constantes. Software utilizado: Statistica v 12.
En la figura 3 se ha representado la regresión lineal de gasto trimestral real frente al gasto trimestral estimado para los modelos ARIMA (3,1,0) a partir de las ecuaciones de la tabla 3.
En la tabla 4 se detallan los resultados obtenidos para el gasto trimestral anual del año 2017, para cada análisis autorregresivo, utilizando las ecuaciones propuestas en la tabla 2. El signo del error indica la desviación que se ha tenido con relación al valor real. Un signo negativo indica que el modelo es insuficiente o escaso y un signo positivo indica que el modelo se ha desbordado. No obstante, aunque el seguimiento trimestral presenta errores ciertamente importantes, el resultado final es lo realmente interesante. Para el modelo ARIMA (3,1,0), sin variable externa, un error anual total pronosticado de -1.3% puede considerarse muy aceptable, si se tiene en cuenta la tremenda incertidumbre que mueve el expediente de gasto de gases en el que se encuentran presentes un gran número de unidades aéreas, cada una de ellas generando su propia fuente de error.
Tabla 4 Resumen de los valores obtenidos en la verificación y seguimiento de cada ARIMA (3,1,0) para los gastos trimestrales y acumulados anuales. Los datos de gasto son los que se incorporarán al modelo ARIMA para el año 2018 (de forma anual o trimestral) y se utilizarán para realizar seguimientos trimestrales y nuevas previsiones para años sucesivos. Fuente: elaboración propia.

DISCUSIÓN
Uno de los problemas iniciales es estimar que modelo ARIMA utilizar. Los parámetros se obtienen de forma que la suma cuadrática de los errores sea la menor. La estimación no es sencilla y muchas ocasiones es necesario utilizar métodos iterativos de estimación no lineal10. Se han planteado pruebas para validar el modelo autorregresivo elegido y verificar si se ajusta realmente al conjunto de los datos reales. Entre los más destacados se encuentra el denominado modelo de sobreparametrización7. Básicamente, consiste en estimar el modelo a un orden superior al que se ha elegido y comprobar que los parámetros obtenidos son o no significativamente diferentes de cero. Si el modelo es correcto los residuos se comportan como ruido blanco y si no, se comportan como ruido autocorrelado. Muy utilizadas son las funciones de autocorrelación de los residuos. Estas funciones tienen que ser significativamente nulas en todo su recorrido. Test, como el Q de Box-Pierce o el Q de Ljung-Box son muy apropiados para comprobar si los residuos obtenidos son conformes con un ruido blanco7. A partir de los errores determinados para el gasto total real se ha elegido como apropiado para realizar estimaciones el modelo ARIMA (3,1,0). En la figura 4 se han representado los correlogramas4 para los residuos. Se observa que las autocorrelaciones residuales no son significativas (están dentro de las bandas de error). Además, para este modelo autorregresivo, se rechaza la hipótesis nula de autocorrelación global, ya que el valor del estadístico Q de Ljung-Box es menor que el punto crítico tabulado. Todo ello hace considerar a los residuos como ruido blanco (no existe autocorrelación) y se confirma la validez predictiva del modelo ARIMA (3,1,0).
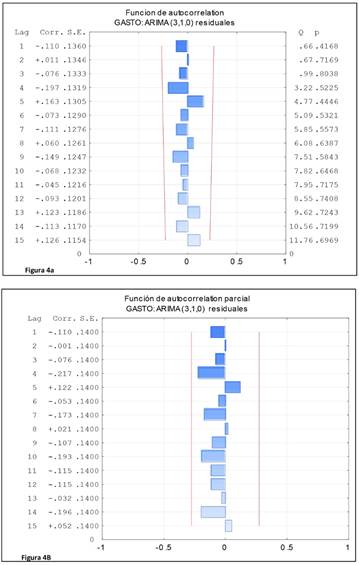
Figuras 4a y 4b Correlograma para los residuos obtenidos en el modelo autorregresivo ARIMA (3,1,0). Las líneas rojas indican el límite de confianza calculado para el error estándar y suponer que los elementos residuales se pueden considerar ruido blanco. En la función de autocorrelación se ha indicado el valor del estadístico Q (Ljung-Box) para cada uno de los retardos considerados. Figura 4a. Modelo ARIMA (3,1,0); Figura 4b. Modelo ARIMA (3,1,0) con variable exógena. Software utilizado: Statistica V 12 y Eviews® 10.
A partir de los modelos autorregresivos se obtienen ecuaciones y modelos matemáticos que explican el comportamiento y estructura de la serie y permiten realizar prospectiva. Las ecuaciones aquí obtenidas, del modelo ARIMA (3,1,0), están ayudando a realizar estimaciones, bastante ajustadas, sobre los requerimientos de gases que las diferentes unidades aéreas precisan para su operatividad. Es necesario recordar que los ARIMA empleados se basan en la premisa de invariancia o estabilidad de la serie. Cualquier modificación, no prevista, que altere de manera notable la serie temporal implica nuevo modelo matemático de predicción, estudio de posible estacionalidad y constancia temporal, tendencias, correlaciones, etc. El modelo calculado se corresponde con el gasto conjunto total de todas las unidades aéreas incorporadas a los expedientes de gases del Ejército del Aire y que en la actualidad son 31. La desagregación de los gastos para cada una de ellas, ha permitido elaborar modelos autorregresivos de estimación de gasto individualizado por unidad. El seguimiento y validación de las estimaciones realizadas se está efectuando a partir de los gastos reales ejecutados durante el año 2018. En la tabla 5 se muestran los datos obtenidos para gasto real y gasto estimado por el modelo ARIMA (3,1,0) durante el año 2018. La reducción del error cometido con respecto al que se obtuvo en el primer trimestre del año 2017 parece indicar que las previsiones realizadas son adecuadas. No obstante, será a la finalización económica del año 2018 cuando se establecerá un mejor análisis sobre la prospectiva total de la evaluación trimestral y anual realizada.
Tabla 5 Gasto real y gasto estimado utilizando el modelo ARIMA (3,1,0) para el primer trimestre y primer mes del segundo trimestre del año 2018 (deflación trimestre 1 de 2018: 1.008; deflación mes abril 2018: 1.017). Elaboración propia. Fuente para deflación: Instituto Nacional de Estadística.
| 2018 Trimestre | Gasto real (€) | Gasto estimado (€) | Error (%) |
|---|---|---|---|
| 1 | 173565,58 | 195953.79 | +12,90 |
| 2 (mes de abril) | 58463.71 | 52718.17 | -9.82 |
| Total | 232029.29 | 248671,96 | +7.17 |
Es necesario destacar que para las series temporales aquí estudiadas se están realizando otro tipo de estudios con modelos autorregresivos de carácter estacional. Este tipo de modelos se denominan SARIMA o SARIMAX, dependiendo de si son estacionales, con ausencia o presencia de variable exógena. Los resultados obtenidos son muy prometedores. Otros estudios han obtenido ecuaciones simplificadas de gasto agregado para este tipo de situaciones11. Así, se ha encontrado que resulta muy útil para estimar rápidamente el gasto trimestral conjunto la ecuación Y=e12±e10 (Y: gasto trimestral; e= 2.718). Para el gasto mensual agregado la ecuación es Y=e11±e8 y el gasto anual total se calcula por la ecuación Y=n*(4*e12±e11) (n: número de años; 1≤n≤4). Estas ecuaciones no son series temporales, pero han resultado muy apropiadas para la detección de errores en los modelos de previsión o desviaciones en el gasto acumulado estimado por ARIMA (3,1,0).
Anteriormente se indicó que los modelos autorregresivos integrados de medias móviles no son los únicos modelos de predicción en series temporales que existen. Los análisis empleando los modelos de vectores autorregresivos (VAR) para corregir las correlaciones espurias o modelos de vectores con corrección del error (VEC), basados en un equilibrio a largo plazo entre variables que, en el corto plazo no existe, son muy utilizados en el campo económico, aunque también se utilizan en otros campos de carácter analítico e interpretativo12. Otros, como los métodos de Holt y Winters también son muy útiles para la interpretación y estudio de pronóstico en series temporales de carácter estacional y que muestran tendencia. Sin embargo, los ARIMA son matemáticamente muy intuitivos y permiten estudiar el comportamiento de una gran variedad de series temporales y modelar algunas de las más importantes fuentes de error que en ellas se encuentran. Las correcciones de tendencias (invariabilidad en el tiempo), estimaciones de estacionalidad o la visualización de errores aleatorios hacen de estos modelos de los más versátiles y utilizados para realizar pronóstico y estimación futura.
CONCLUSIÓN
El seguimiento económico de los expedientes de contratación para el suministro de oxígeno de vuelo, otros gases y elementos asociados para el Ejército del Aire que realiza el personal farmacéutico del Centro de Farmacia del Aire de Madrid es de gran importancia. Los modelos autorregresivos de medias móviles (ARIMA), por su versatilidad, están resultando de gran ayuda en la realización de las estimaciones económicas de los expedientes de gases que es necesario plantear. Un modelo sencillo, que cumple con los requisitos matemáticos establecidos, es el modelo ARIMA (3,1,0), sin variable externa. Con este modelo se puede realizar seguimiento de gasto de manera trimestral, y por desagregación o agregación, también de forma mensual o anual, respectivamente.
Durante el tiempo (6 trimestres) que se lleva realizando el seguimiento mediante el modelo ARIMA deducido en este trabajo no se han producido desajustes importantes entre lo calculado y lo gastado.
En el año 2019 se ha de proponer un nuevo expediente para la gestión analítica y económica del oxígeno de vuelo y elementos asociados utilizados en el Ejército del Aire, y las ecuaciones de gasto predictivo obtenidas aquí y mejoradas a partir de nuevos datos, una vez aplicados los términos correctores anuales, servirán para plantear la prospectiva de gasto que se marcó como objetivo principal de este trabajo y que no es otro que la de estimar correctamente, con la enorme dificultad que implica, qué asignación económica total se prevé para un expediente de contratación que tiene, hasta el momento, 31 unidades aéreas y una duración media de 4 años.













