Mi SciELO
Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Escritos de Psicología (Internet)
versión On-line ISSN 1989-3809versión impresa ISSN 1138-2635
Escritos de Psicología vol.2 no.3 Málaga ago. 2009
¿Qué código subyace a las Multiplicaciones? Evidencias de una tarea de magnitud con priming enmascarado
Which code does underlie multiplication? Evidences from a magnitude decision task with masked priming
Jesús Damas López
Nesplora Neuroscience Support Systems S.L.
Dirección para correspondencia
RESUMEN
Estudios recientes han mostrado que la presentación previa y enmascarada de una multiplicación favorece la denominación del resultado de ésta. Los diferentes modelos de procesamiento aritmético que coexisten actualmente ofrecen explicaciones distintas a este fenómeno, no estando claro cuál es el locus (semántico o verbal) de este efecto de facilitación. En el presente estudio intentamos determinar la naturaleza del efecto manteniendo la secuencia de exposición, pero variando la tarea, cambiando la tarea verbal de denominación por una tarea semántica de decisión de magnitud ("¿es el número que aparece en pantalla mayor o menor que 18?"). Se presentaron una serie de números target precedidos de una multiplicación enmascarada, coincidente o no con el número target sobre el que se debía realizar el juicio de magnitud. El tiempo en juzgar la magnitud de los targets fue similar tanto si la multiplicación previa tenía como resultado el target como si no. Así, la presentación de una multiplicación enmascarada no parece activar su solución a nivel semántico, lo que sugiere que el locus de los efectos de priming de multiplicación encontrados en las tareas de denominación tiene su origen en las representaciones verbales de las multiplicaciones.
Palabras clave: Priming enmascarado, multiplicaciones simples, tarea de decisión de magnitud.
ABSTRACT
Recent studies have shown that the prior masked presentation of a multiplication facilitates the naming of its solution. The different models of arithmetical processing that coexist today offer various explanations for this phenomenon, and it is not clear what is the locus (semantic or verbal) of this facilitation effect. In the present study we try to determine the nature of the effect by keeping the same exposition sequence, but changing the naming verbal task to a magnitude decision task ("is the number displayed more or less than 18?"). We presented a series of target numbers preceded by a masked multiplication matching or non-matching the target number on which the magnitude judgement should be done. The time to judge the magnitude of the matching targets was similar to that taken to judge the non-matching ones. Thus, the presentation of a masked multiplication does not appear to activate its solution at the semantic level, suggesting that the locus of the priming effects found in naming tasks has its origin in the verbal representations of the multiplication.
Keywords: Masked priming, single-digit multiplications, magnitude decision task.
A pesar de la importancia de los procesos cognitivos implicados en el cálculo numérico, no son demasiados los estudios dedicados a este tema en comparación con los que estudian otros procesos cognitivos como, por ejemplo, el lenguaje. Así, mientras que los modelos de procesamiento del lenguaje están bastante bien asentados, no ocurre lo mismo con los modelos de procesamiento de números arábigos o de operaciones aritméticas.
La aritmética implica distintos procesos cognitivos y estrategias dependiendo del tipo de operación, símbolo numérico usado, etc. Parece claro que el procesamiento de números en su forma arábiga es asimétrico con respecto al de números en su forma verbal (ver Damián, 2004). Por otra parte, Cappelletti y sus colaboradores (Cappelletti, Butterworth y Kopelman, 2001) sugieren que el dominio aritmético semántico es independiente de cualquier otro dominio semántico, aunque no está claro si dentro de ese conocimiento semántico-aritmético pueden distinguirse o no distintos subsistemas, con contenidos puramente numéricos por un lado y con contenidos léxicos por otro (ver Salguero, Lorca y Alameda, 2004).
Lo que parece intuitivo es que los procesos aritméticos están relacionados de alguna manera con los procesos lingüísticos: aprendemos a multiplicar con estrategias verbales; contar es aparentemente una tarea verbal pura; los números también son, en definitiva, palabras... Sin embargo, esta relación entre lenguaje y aritmética no está clara. Varios autores (Dehaene y Cohen, 1995; Delazer y Bartha, 2001; Lee y Kang, 2002) defienden que el lenguaje estaría implicado en tareas como contar o leer números en voz alta, pero también en el cálculo de multiplicaciones, no estando implicado en otras operaciones aritméticas. Pero por otra parte ciertos autores defienden la independencia del cálculo aritmético con respecto del lenguaje (De Rammelaere, Stuyven y Vandierendonck, 2001; García-Orza, León-Carrión y Vega, 2003; McCloskey, 1992).
Para intentar dar explicación a los resultados que se han obtenido hasta ahora en relación con el procesamiento aritmético, y dar una descripción de la relación entre el mismo y los procesos lingüísticos, se han propuesto diversos modelos.
El modelo de McCloskey (1992; McCloskey, Caramazza, y Basili, 1985) constituye el primer intento serio desde la neuropsicología cognitiva de descripción de los procesos psicológicos implicados en el procesamiento numérico y aritmético, desde el reconocimiento de números en sus distintas formas de expresión y su producción hasta el cálculo de operaciones. Aunque ha sufrido alguna pequeña variación desde su elaboración inicial (McCloskey et al., 1985), mantiene su estructura básica (McCloskey, 1992).
De acuerdo con este modelo, dentro de la identificación y la producción de los símbolos numéricos se distinguiría una forma arábiga, de carácter visual, y una forma verbal, que incluiría la forma fonológica y escrita de los números. Las operaciones aritméticas, desde la recuperación de hechos numéricos hasta el cálculo mental, se llevarían a cabo utilizando una representación abstracta unitaria de cantidad, independiente del código en el que se presente el input. Ello implica necesariamente que cualquier hecho numérico, antes de ser procesado, ha de ser traducido a ese código abstracto por módulos específicos, igual que otros módulos específicos se encargarían de traducir ese código abstracto a otros códigos (verbal o arábigo) en la producción numérica. Así, al ser demandada la resolución de un determinado hecho aritmético u operación simple, éste pasaría por el sistema de comprensión de números arábigos o verbales, dependiendo de la notación en la que estuviese expresado; después se accedería a la representación abstracta, la cual nos serviría para realizar un cálculo, si es oportuno; y, finalmente, se expresaría el resultado pasando por uno de los módulos (verbal o arábigo) de producción de números.
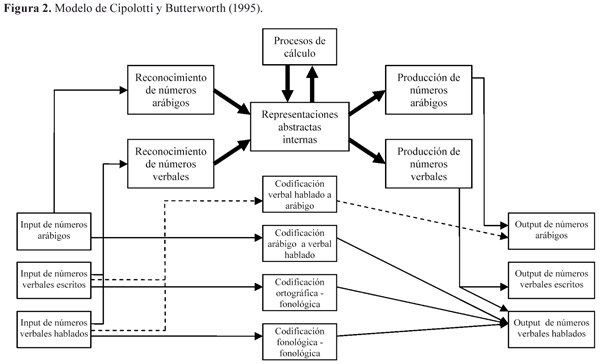
Otros modelos rechazan explícitamente la hipótesis de McCloskey relativa al papel central de la representación abstracta en todos los procesos aritméticos. Algunos autores sugieren la existencia de una ruta asemántica para la transcodificación entre notaciones numérica y verbal sin pasar por una representación semántica intermediaria. Cipolotti y Butterworth (1995), en su modelo de multi-ruta, proponen que tenemos un sistema de representaciones abstractas que se utiliza para hacer cálculos, pero que no tiene porqué ser utilizado, por ejemplo, para hacer tareas de lectura y escritura al dictado de números arábigos. El modelo sería una extensión del modelo de McCloskey, añadiéndole a éste rutas asemánticas que permiten la conversión entre unos códigos y otros sin acceder a la representación semántica del número. Se utilizaría una ruta u otra dependiendo de las demandas de la tarea, siendo inhibidas las rutas distintas a la activada.
El modelo de triple código de Dehaene (1992; Dehaene y Cohen, 1995), por último, asume que hay tres categorías de representación mental en las que los números pueden ser manipulados por el sistema cognitivo. Una sería la forma visual del número arábigo, la cual estaría formada por una cadena de dígitos. Otra sería la forma verbal, la cual estaría formada por una secuencia de palabras organizadas sintácticamente, y podría estar relacionada con el cálculo de multiplicaciones. Ni la forma visual ni la verbal contendrían información semántica; ésta sólo estaría en la representación analógica de la magnitud, que contendría la información que nos permite, por ejemplo, hacer estimaciones, comparaciones entre dos números, o restar. Según el modelo, el acceso a cualquiera de los tres tipos de representación puede ser directo, dependiendo del tipo de estímulo: un conjunto de objetos puede evocar el acceso directo a su magnitud asociada, un número arábigo provocará la activación de su forma visual a través del sistema de reconocimiento visual del sistema cognitivo y, por su parte, la forma verbal estaría conectada a los sistemas lingüísticos de reconocimiento de palabras. Además, se establecen conexiones directas entre ellos, de forma que se podría acceder rápidamente a una magnitud a partir de un número arábigo o de su forma verbal y viceversa, a la vez que se podría pasar de la forma verbal a la visual o al contrario sin acceder a la representación de la magnitud.
Existen escasos estudios sobre la relación entre el procesamiento numérico, o más concretamente, el cálculo, y el lenguaje. Las conclusiones que arrojan los resultados de estos estudios pueden ser útiles para plantear cuál de los modelos de procesamiento aritmético comentados anteriormente es el que mejor describe los procesos de cálculo y reconocimiento numéricos, y para determinar la implicación del lenguaje en los mismos.
Delazer y Bartha (2001) hacen una revisión de diversos estudios de caso único de pacientes con afasia y encuentran que muchos de ellos tenían problemas en tareas como contar o leer números en voz alta, y también problemas para el cálculo de multiplicaciones, en contraste con la preservación de la habilidad para otras operaciones aritméticas. Estos datos, que sugieren la existencia de una relación entre la multiplicación y el lenguaje, pero no entre el lenguaje y otras operaciones aritméticas, son favorables al modelo de Dehaene y Cohen (1995).
Por otra parte, García-Orza y colaboradores (2003) encontraron en su paciente JS una disociación entre el cálculo básico y la lectura de números arábigos. Este paciente, que sufría anomia, dislexia fonológica y graves problemas de escritura, cometía numerosos errores a la hora de nombrar números arábigos, pero mostraba una buena comprensión numérica probada por su buen rendimiento en tareas de comparación de números o de cálculo de operaciones aritméticas simples. Esto sugiere que ese cálculo puede ser independiente del procesamiento lingüístico. En concreto, la multiplicación no requeriría la activación de la forma fonológica de los operandos, constituyendo un dato en contra del modelo de Dehaene y Cohen (1995).
También en contraste con la idea de que los hechos aritméticos utilizan una forma verbal dependiente del sistema lingüístico, De Rammelaere y sus colaboradores (De Rammelaere et al., 2001) encuentran, por medio de experimentos con participantes sanos y utilizando un paradigma de doble tarea, que el bucle fonológico no parece estar implicado en la verificación de operaciones aritméticas simples. Sin embargo, Lee y Kang (2002), usando igualmente un paradigma de doble tarea con participantes sanos, encuentran que la supresión articulatoria disminuye significativamente el rendimiento en tareas de multiplicación y no en tareas de resta, resultado a favor de la postura de Dehaene (1992; Dehaene y Cohen, 1995); sin embargo, Damas y García-Orza (2004) no pudieron replicar estos resultados.
Reynvoet, Brysbaert y Fias (2002), por medio de experimentos con un paradigma de priming semántico, encuentran datos que apuntan a la rápida implicación de la semántica en la denominación de números, lo que apoya que, aunque la resolución de las multiplicaciones pueda ser muy rápida, esto no es óbice para que, como propone modelo de McCloskey (1992), haya implicación de la semántica.
En una investigación publicada recientemente (García-Orza et al., 2009) encontramos, utilizando un paradigma de priming enmascarado, que la exposición a una multiplicación (representada con la forma arábiga de los números) durante un breve espacio de tiempo mejora el tiempo de lectura en voz alta del número resultado de la operación (en comparación con la lectura de ese mismo número cuando va precedida de una operación cuyo resultado no coincide con ese número). Así por ejemplo, si se presenta "2x3" y después "6", éste número se lee más rápido que si se hubiese presentado "2x5" y luego "6". Este fenómeno podría explicarse desde el modelo de McCloskey (1992) si pensamos que la presentación previa del prime activa el resultado de la multiplicación en el sistema de representaciones abstractas, y esta activación es aprovechada en el proceso de lectura del número target, haciendo más rápida su lectura. También podría explicarse por el modelo de Dehaene y Cohen (1995), si tenemos en cuenta que el sistema encargado de la lectura en voz alta del target es el mismo que el que se encargaría de realizar la operación de multiplicación, de forma que el sistema aprovecharía la activación de la representación verbal producida por la presentación de la multiplicación para facilitar el proceso de lectura. Desde el modelo de Cippolotti y Butterworth (1995) habría más dificultades para dar una explicación a este efecto, pues habría que pensar que en el breve lapso de tiempo que existe entre la presentación del prime y la presentación del target -50ms de SOA (stimulus-onset asynchrony ó asincronía estimular)-, el sistema tendría que resolver la operación usando un código abstracto y posteriormente activar la representación del resultado de la multiplicación a nivel fonológico.
Esto permitiría que cuando llegara el proceso de denominación del número por una vía asemántica pudiera existir algún tipo de facilitación.
Para intentar determinar qué modelo explica mejor el fenómeno, en el presente estudio decidimos mantener la secuencia de exposición empleada en el estudio de García-Orza et al. (2009) pero variando la tarea: en vez de usar una tarea de denominación usamos una tarea de tipo semántico. Presentamos una serie de multiplicaciones enmascaradas, precediendo cada una a un número que el participante tenía que juzgar si era mayor o menor que 18. El número a evaluar podía o no ser el resultado de la multiplicación que le precedía.
Como control utilizamos también primes de repetición, e incluimos dos condiciones de asincronía estimular (SOA de 67 y 150ms respectivamente) con objeto de explorar el curso temporal de la tarea, pero manteniendo la garantía de automaticidad del proceso. Así, cambiando la lectura en voz alta de los números por una tarea de comparación de magnitud (que exige semántica), podríamos saber si la mera exposición a una multiplicación con sus números escritos en forma arábiga puede dar acceso automático a la representación semántica del resultado de la operación y por tanto facilitar la tarea de juicio de magnitud. Si esto ocurriese,
no podría ser explicado por el modelo de Dehaene y Cohen (1995), ya que las rutas cognitivas implicadas en la multiplicación y en la decisión de magnitud son diferentes, no dejando lugar a que un proceso influya sobre el otro.
Sin embargo, sí que podría explicarse con el modelo de McCloskey (1992), pues la ruta cognitiva sería la misma que para la lectura (y la explicación sería equivalente desde el modelo de Cippolotti y Butterworth (1995), ya que los módulos implicados serían los mismos que en el modelo de McCloskey (1992)).
Método
Participantes
Veintiséis estudiantes de la facultad de Psicología de edades comprendidas entre 21 y 28 años (M=23.44) participaron voluntariamente en el experimento. De ellos, 22 eran mujeres y 4, hombres. Todos los participantes tenían una visión normal o corregida en el momento de hacer el experimento y eran diestros. Todos los procedimientos experimentales se realizaron siguiendo las normas éticas de la APA (2002).
Aparatos y materiales
Los estímulos eran presentados en una pantalla de ordenador de un tamaño de 17" y una tasa de barrido de aproximadamente 16.6 ms (60 Hz), por medio del software E.R.T.S. (Experimental Run-Time System) versión 3.30 (Beringer, 1999). Los participantes daban sus respuestas mediante las teclas 'A' y 'L' del teclado.
Como targets se seleccionaron 10 números arábigos entre '6' y '30', 5 mayores de '18' y 5 menores de '18', que fueron presentados con caligrafía tipográfica y tamaño de 42mm. Antes de ellos aparecían como primes enmascarados multiplicaciones (representadas como "[dígito]x[dígito]=") cuyo resultado podía ser o no el número target. Las multiplicaciones siempre fueron de un solo dígito por otro, distintos entre sí y distintos de '0' y '1'. La distancia numérica entre cada target por encima de '18' y dicho número fue pareada con cada uno de los targets por debajo (excepto '10' y '28'; ver Tabla 1). Se incluyó también una condición de control o de priming de repetición, en la que los targets iban precedidos de los números arábigos resultado de las multiplicaciones.
En la condición coherente los targets coincidían con el resultado de la operación que mostraba el prime o con el propio prime (en el priming de repetición). En la condición incoherente el target era el número cuya distancia numérica a '18' es la misma que entre el prime y '18', pero con distinto estatus (i.e. mayor vs. menor); por ejemplo, el target correspondiente al prime '15' era '21' (ver Tabla 1).
Procedimiento
La tarea experimental está basada en el procedimiento de Greenwald et al. (Greenwald et al., 2003). De forma previa al experimento propiamente dicho, los participantes debían solucionar las operaciones aritméticas de una hoja que se les suministraba, a modo de entrenamiento. Las operaciones incluían 25 restas, 25 multiplicaciones, y 25 números a copiar, y entre ellas aparecían las operaciones que posteriormente serían utilizadas como estímulos en la fase experimental. También antes de la tarea experimental, los participantes completaban un sencillo cuestionario sobre su aprendizaje aritmético y lingüístico y su capacidad visual, para asegurar que todos tenían una buena capacidad perceptiva y para descartar a aquellos que pudieran presentar problemas de discalculia.
En la tarea de ordenador los participantes se situaban a una distancia de unos 60 cm. del monitor. Al principio de la tarea aparecían en la pantalla unas simples instrucciones que indicaban al participante que tenía que juzgar si el número que aparecía en la pantalla era mayor o menor que 18.
En cada ensayo aparecía una máscara formada por cuatro almohadillas (####) durante 300ms, después el prime durante dos barridos de pantalla (aprox. 33ms.) y después de nuevo la máscara durante un tiempo variable (dependiendo del SOA del ensayo). Finalmente, aparecía el número a evaluar, el target, durante 450ms., después de los cuales era sustituido por un símbolo de interrogación, sugiriendo al participante que indicase su juicio.

La tarea experimental se dividió en dos sesiones. De forma previa a cada una de ellas se presentaron 20 ensayos de práctica (no considerados en el análisis). Los ítem que aparecían en la sesión de práctica eran distintos a los empleados en las sesiones experimentales aunque similares (otros dígitos).Las dos sesiones experimentales, ambas de 80 ensayos, se diferenciaban en que en cada una (y en sus correspondientes ensayos de práctica) las teclas de respuesta se usaban de forma inversa, con objeto de controlar posibles efectos de destreza: en una, la tecla "A" servía para juzgar menor que 18 el número que aparecía en pantalla, y para juzgarlo mayor se usaba la tecla "L"; en la otra era al contrario. El orden de las sesiones experimentales fue contrabalanceado.
En cada sesión experimental se presentaban los diez targets, cinco menores que 18 y cinco mayores, ocho veces cada uno. En la mitad de las ocasiones (un bloque) el tiempo de aparición de la segunda máscara era el de dos barridos de pantalla (33ms. aprox., SOA de 67ms.), y en la otra, aprox. 120ms. (SOA de 150ms.), y dichos bloques fueron contrabalanceados. Dentro de cada bloque, los 10 targets iban dos veces precedidos por multiplicaciones, una vez por multiplicaciones coherentes y otra por multiplicaciones incoherentes, y otras dos por números arábigos, que podían ser iguales al target (coincidiendo con el resultado de las multiplicaciones coherentes) o diferentes al target (coincidiendo con el resultado de las multiplicaciones incoherentes).
Resultados
Para el análisis sólo se tuvieron en cuenta las respuestas correctas. Dado el escaso número de errores (el 2.67% del total), no se procedió al análisis de los mismos. También se establecieron puntos de corte en 3000 y 1500 ms. y fueron despreciados los tiempos de respuesta fuera de ese rango (2.26%). Además, uno de los 26 participantes fue eliminado por tener el 20% de las respuestas fuera del rango válido. Las medias de los tiempos de respuesta obtenidos por el resto de los participantes se muestran en la tabla 2.
Se procedió a un análisis de la varianza de medidas repetidas, en el que las teclas de respuesta, el SOA, el tipo de prime y la coherencia con el target eran factores intrasujeto. Ninguno de los factores principales resultó significativo, excepto el factor tipo de prime, siendo superiores los tiempos de respuesta en la condición en la que el target iba precedido de una multiplicación que en la que iba precedido de un número (F(1,24)=6.03; p< .05).
El análisis de las interacciones de segundo y tercer orden no mostró resultados significativos (todas las F<1), excepto la interacción entre el factor tipo de prime y el factor de coherencia: en la condición de prime de repetición el efecto de la coherencia fue distinto que en la condición de prime de multiplicación (F(1,24)=9.10; p< .01). Cuando el prime fue de repetición, el análisis mostró que los participantes respondieron significativamente más rápido (24 ms) cuando el prime era coherente que cuando no lo era (t(24)=-3.15; p< .05). Por otra parte, cuando el prime fue una multiplicación no se observaron diferencias significativas entre los tiempos de respuesta con prime coherente y con prime no coherente (t(24)=-0.12; p=0.90).

Efecto de distancia
En experimentos de comparación de magnitud de números se ha encontrado repetidamente el llamado efecto de distancia semántica (o numérica), que consiste en que cuando hay que decidir entre dos números cuál es mayor o menor, las respuestas son más rápidas cuanto mayor es la distancia numérica entre los dos números (Brysbaert, 1995; Dehaene, 1990; Moyer y Landauer, 1967, cit. Koechlin et al., 1999; Reynvoet, Brysbaert y Fias, 2002).
A continuación, con el objetivo de evaluar el efecto de distancia en nuestros datos y comprobar así la robustez de nuestro diseño, realizamos un ANOVA estatus numérico x distancia x tipo de prime x coherencia. Incluimos también en el análisis la variable estatus numérico (estar por encima o por debajo de 18) porque consideramos que podía jugar un papel importante en el proceso de comparación. La variable 'distancia' resultó claramente significativa (F(3,72)=21.36; p< .01). También resultó significativa la interacción estatus numérico x distancia (F(3,72)=3.66; p< .05), lo que quiere decir que el efecto de distancia se daba de forma diferente en los números mayores de 18 que en los menores. Dicho de otra forma, la interacción indica que aun siendo significativa la distancia en ambas condiciones, es menor la influencia de la misma dentro del grupo de números mayores que 18 (F(3,72)=5.38; p< .01) que en el grupo de los números menores que 18 (F(3,72)=17.11; p< .01), lo cual apoya la idea de Dehaene y Cohen (1995) de que la representación de magnitud sigue una progresión logarítmica (i.e. hay mayor distancia entre el 1 y el 2 que entre el 31 y el 32).
La interacción distancia numérica x coherencia asimismo resultó significativa (F(3,72)=3.72; p< .05). Aunque tanto en coherentes como en incoherentes se observó el efecto de distancia (respectivamente, F(3,72)=19.33; p< .01 y F(3,72)=6.41; p< .01) en el caso de los ítem coherentes (fueran los primes multiplicaciones o números arábigos) la distancia entre el target y 18 fue más decisiva a la hora de suponer una facilitación o inhibición del juicio de comparación que para los ítem no coherentes.
El resto de interacciones con la variable distancia numérica no resultó significativo.
Discusión
Esta investigación se enmarca en un proyecto que trata de analizar la implicación de los códigos lingüísticos en la resolución de operaciones aritméticas. En el presente experimento, el objetivo concreto era contrastar la relación entre la semántica y la resolución de multiplicaciones simples. Para ello llevamos a cabo un experimento de priming enmascarado, en el que los participantes tenían que realizar juicios de magnitud acerca de una serie de números presentados (en su forma arábiga) en una pantalla de ordenador, habiéndose presentado antes de cada uno la multiplicación cuyo resultado es dicho número o uno no relacionado. Como control utilizamos priming de repetición: el target podía ir precedido de un número arábigo igual o diferente.
Los resultados indican que se produce un efecto de facilitación cuando el prime y el target son exactamente el mismo número, efecto que se ha encontrado en otros estudios similares (Koechlin et al., 1999; Naccache y Dehaene, 2001; Reynvoet, Brysbaert, Fias, 2002), pero no encontramos efectos de priming al utilizar las multiplicaciones como prime. Esto es, hay una disminución significativa del tiempo que tardan los participantes en juzgar si un número es mayor o menor que 18 cuando antes del número a juzgar se presenta de forma enmascarada el propio número (en comparación con cuando se presenta un número distinto). Sin embargo, no encontramos diferencias significativas cuando presentamos como prime la multiplicación que da como resultado el número a juzgar (con respecto a cuando presentamos una multiplicación cuyo resultado es de distinto estatus numérico que el número a juzgar).
Estos resultados son compatibles con el modelo de triple código de Dehaene y Cohen (1995), dado que el procesamiento de la multiplicación se llevaría a cabo en el sistema de representaciones verbales, y para ello habría que acceder al código lingüístico, mientras que el número target sobre el que hay que hacer el juicio de magnitud se codificaría directamente en su representación abstracta, no viéndose facilitada su activación por el procesamiento de la multiplicación. Por el contrario, desde el modelo de McCloskey (1992; y de forma equivalente en el modelo multirruta de Cipolotti y Butterworth, 1995) sí se hubiese esperado cierta facilitación, pues dado que el camino para el procesamiento del target es el mismo que para el prime, el sistema ya tendría que haber activado la representación analógica del target antes de ser procesado. Así, nuestros resultados sugieren que no existe solapamiento entre los procesos implicados en la resolución de multiplicaciones y aquellos implicados en la decisión de magnitud sobre un número arábigo.
Los hallazgos, por un lado, del clásico efecto experimental de distancia (Brysbaert, 1995; Dehaene, 1990; Moyer y Landauer, 1967, cit. Koechlin, Naccache, Block, y Dehaene, 1999; Reynvoet, Brysbaert y Fias, 2002) y, por otro, del efecto de priming de repetición, garantizan la potencia de nuestro experimento y sugieren que la ausencia de efectos de priming con multiplicaciones se debe a que los códigos empleados en la resolución de multiplicaciones difieren de los empleados en el juicio sobre su magnitud, y no son debidos a falta de potencia de nuestro diseño. De forma similar, la ausencia de efectos con diferentes SOAs permite descartar que los efectos de facilitación semántica tengan lugar con un curso temporal diferente al empleado en la tarea de denominación.
La importancia de los procesos verbales en relación con el procesamiento aritmético no está bien establecida. Se han propuesto distintos modelos para intentar explicar la forma en la que procesamos los hechos numéricos y el papel que juegan los códigos lingüísticos dentro de ese procesamiento.
En concreto, a la hora de resolver multiplicaciones simples, el modelo de triple código de Dehaene y Cohen (1995) asume que se utilizan códigos verbales, mientras que otros modelos como el de McCloskey (1992; McCloskey et al., 1985) o el modelo multirruta de Cipolotti y Butterworth (1995) asumirían que para realizar cualquier operación, incluyendo la multiplicación, habría que acceder antes a la representación abstracta de los operandos.
Nuestros resultados estarían a favor del modelo de Dehaene y Cohen (1995), pues mientras que encontramos cierta facilitación para la tarea verbal de leer un número presentando antes la multiplicación cuyo resultado es ese número (García-Orza et al., 2009), no ocurre lo mismo cuando la tarea a realizar es de índole semántica. Esto es, la activación previa del resultado de la multiplicación no es aprovechada en la tarea de juicio de magnitud y sí en la de denominación, indicando que la presentación previa de la multiplicación activa una representación de tipo verbal que sí es aprovechada cuando la tarea es de tipo verbal y no cuando es de tipo semántico. Así, los datos sugieren que la resolución de multiplicaciones simples es una tarea automática que se produce mediante la activación de representaciones de tipo verbal.
Referencias
American Psychological Association (2002). Ethical Principles of Psychologists and Code of Conduct. (2002). American Psychologist, 57, 1060-107. [ Links ]
Beringer, J. (1999). Experimental run time system (ERTS), version 3.30. Frankfurt: Berisoft. [ Links ]
Brysbaert, M. (1995). Arabic Number Reading: On the Nature of the Numerical Scale and the Origin of Phonological Recoding. Journal of Experimental Psychology: General, 124, 434-452. [ Links ]
Cappelletti M., Butterworth, B. y Kopelman, M. (2001). Spared numerical abilities in a case of semantic dementia. Neuropsychologia, 39, 1224-1239. [ Links ]
Cipolotti, L., Butterworth, B. (1995). Toward a multiroute model of number processing: impaired number transcoding with preserved calculation skills. Journal of Experimental Psychology: General, 124, 375-390. [ Links ]
Damas, J. y García-Orza, J. (2004, abril). Multiplicaciones simples y códigos verbales: Evidencias desde el estudio de sujetos sanos. Póster presentado en el V Congreso de la Sociedad Española de Psicología Experimental (SEPEX). Madrid. [ Links ]
Damian, M.F. (2004). Asymmetries in the processing of Arabic digits and number words. Memory & Cognition, 32, 164-171. [ Links ]
De Rammelaere, S., Stuyven, E., Vandierendonck, A. (2001). Verifying simple arithmetic sums and products : Are the phonological loop and the central executive involved? Memory & Cognition, 29, 267-273. [ Links ]
Dehaene, S. (1992). Varieties of numerical abilities. Cognition, 44, 1-42. [ Links ]
Dehaene, S. y Cohen, L. (1995). Towards an anatomical and functional model of number processing. Mathematical Cognition, 1, 83-120. [ Links ]
Delazer, M., y Bartha, L. (2001). Transcoding and calculation in aplasia. Aphasiology, 15, 649-679. [ Links ]
García-Orza J., Damas-López J., Matas A, Rodríguez J.M. (2009). "2 x 3" primes naming "6": evidence from masked priming. Attention, Perception and Psychophysics, 71, 471-80. [ Links ]
García-Orza, J., León-Carrión, J. y Vega, O. (2003). Dissociating arabic numeral reading and basic calculation: a case study. Neurocase, 9, 129-139. [ Links ]
Greenwald, A.G., Abrams, R.L., Naccache, L. y Dehaene, S. (2003). Long-Term Semantic Memory Versus Contextual Memory in Unconscious Number Processing. Journal of Experimental Psychology: Learning, Memory and Cognition, 29, 235-247. [ Links ]
Koechlin, E., Naccache, L., Block, E. y Dehaene, S. (1999). Primed Numbers: Exploring the Modularity of Numerical Representations with Masked and Unmasked Priming. Journal of Experimental Psychology: Human Perception and Performance, 25, 1882-1905. [ Links ]
Lee, K-.M., y Kang, S.-Y. (2002). Arithmetic operation and working memory: differential supression in dual tasks. Cognition, 83, 63-68. [ Links ]
McCloskey, M. (1992). Cognitive mechanisms in numerical processing: Evidence from acquired dyscalculia. Cognition, 44, 107-157. [ Links ]
McCloskey, M., Caramazza, A. y Basili, A.G. (1985). Cognitive mechanisms in number processing and calculation: Evidence from acquired dyscalculia. Brain and Cognition, 4, 171-196. [ Links ]
Naccache, L. y Dehaene, S. (2001). Unconscious semantic priming extends to novel unseen stimuli. Cognition, 80, 223-237. [ Links ]
Reynvoet, B., Brysbaert, M. y Fias, W. (2002). Semantic priming in number naming. The Quarterly Journal of Experimental Psychology, 55A(4), 1127-1139. [ Links ]
Salguero, M.P., Lorca, J.A. y Alameda, J.R. (2004, Abril). Conocimiento numérico cuantitativo y léxico: Evidencias de doble disociación. Póster presentado en el V Congreso de la Sociedad Española de Psicología Experimental. [ Links ]
![]() Dirección para correspondencia:
Dirección para correspondencia:
Jesús Damas-López.
Nesplora Neuroscience Support Systems S.L.
Edificio Joxe Mari Korta.
Avda. Tolosa, 72. Donostia-San Sebastián.
jdamas@nesplora.com
Fecha de recepción: 26 de junio de 2009
Fecha de aceptación: 3 de julio de 2009