Introduction
Beliefs about and attitudes concerning mathematics show significant impact on one’s decisions about the amount and nature of mathematics one will study in the future. To state differently, students’ mathematics-related career trajectories are likely to be influenced by their emotions, feelings and self-beliefs toward mathematics. Hence, attitudinal constructs either guide students to study mathematics or mathematics-related fields or they push students away from careers that require even moderate mathematics competencies (Hafner, 2008). As a result, educating learners with strong self-beliefs in mathematics and positive attitudes towards mathematics should be the overarching aim of all educators. Thus, there has been a major shift to study contributions of affective variables, such as self-efficacy, attitudes and dispositions, on cognitive skills (Aiken, 1970; Pajares, 2006; Schunk & Mullen, 2012).
Motivational and emotional variables involving belief, anxiety and attitudes are also important in understanding mathematics achievement (Soleymani & Rekabdar, 2016). Thus, despite the fact that mathematics is viewed as a cognitive discipline, the affective dimension should not be ignored; so, understanding the nature of attitudinal constructs and their relationships with demographic characteristics and mathematics achievement should be a major research concern. In other words, in this research we aimed to investigate how seventh grade students’ academic self-efficacy, mathematics anxiety, attitudes toward mathematics, and mathematics achievement differ according to gender and school type. We also explored how well academic self-efficacy, mathematics anxiety and attitudes toward mathematics together with gender and school type predict mathematics achievement.
Academic self-efficacy beliefs
Academic self-efficacy, how self-efficacy is perceived in school context, is learners’ self- perceived confidence to successfully perform a particular academic task. For students, academic self-efficacy is a critically important belief because it influences one’s choices, effort, persistence, and feelings. Individuals with higher level of self-efficacy show greater effort, persistence and resilience. According to Bandura (1992), self-efficacy beliefs, individuals’ beliefs about their competence, evolve during early childhood as the children encounter different experiences, obstacles, new tasks or difficult situations. An essential characteristic of self-efficacy is that it has a significant relationship with cognitive and non-cognitive constructs, including academic achievement (Schunk & Mullen, 2012). Regarding school mathematics, self-efficacy is found to be one of the most critical variables for explaining difference in mathematics performance of students that explains quarter of the variance while predicting students’ mathematics achievement (Pajares, 2006). Indeed, mathematics self-efficacy is a stronger predictor of mathematics achievement than mathematics anxiety and previous mathematics experience (Pajares & Miller, 1994). In an earlier research, Liu and Koirala (2009) investigated the relationship between mathematics self-efficacy and mathematics achievement of high school students. Results of correlation analysis and survey linear regression analysis indicated that mathematics self-efficacy and mathematics achievement were significantly related. It was also found out that mathematics achievement could be predicted by mathematics self-efficacy scores. More research should be conducted to explore the relationship between mathematics self-efficacy and achievement (Liu & Koirala, 2009). Yet, studies conducted in Turkey and many other contexts have focused on dual relationship between the variables; but, combined effect of attitudinal variables on mathematics achievement have been ignored. As a result, exploring the relationship between mathematics achievement and self-efficacy was selected as one of the focal points of the present study.
Mathematics Anxiety
Mathematics anxiety, a critical factor to explain the nature of mathematics performance, is defined as “feeling tension and anxiety that interferes with the manipulation of numbers and the solving of mathematical problems in a wide array of ordinary life and academic situations” (Richardson & Suinn, 1972, p. 551). A negative relationship between mathematics anxiety and achievement has been reported previously. For instance, Cates, Rhymer, Smith, and Skinner (1998) conducted a research study with undergraduate students to investigate the relationship between mathematics anxiety and mathematics performance related to fluency measures in single digit computations. Data analysis showed that there was negative correlation between student fluency scores (i.e., speed and accuracy of acquisition level material) and mathematics anxiety; but, it was not significant. Elsewhere, it was found out that students with low anxiety finished multidigit problems correctly per minute compared to the students with high anxiety (Cates & Rhymer, 2003). In an earlier study with a set of long-term trend data, Ma and Xu (2004a) found out that junior and senior high school students’ former low performance in mathematics was significantly associated with future high mathematics anxiety. Conversely, the researchers reported that prior high mathematics anxiety was slightly associated with future low mathematics achievement. Thus, their findings were not consistent regarding the relationship between the two concepts and their findings was limited to junior and senior high school students. In another research with 10th grade students Karimi and Venkatesan (2009) examined the relationship between mathematics anxiety and performance. Researchers stated negative significant correlation between mathematics performance and anxiety parallel to the other research studies in the literature (Devine, Fawcett, Szucs, Dowker, 2012; Hembree, 1990; Ma, 1999). Based on the above literature we could deduce that although several research studies have been carried out regarding mathematics anxiety, little attention was given to younger students (Bonnstetter, 2007). Newstead (1998) stressed that mathematics anxiety begins at early age. When the mathematics instruction at early ages focuses on alternative teaching methodologies like problem solving and encourages students’ informal discussions, students’ mathematics anxiety would be lower than the mathematics anxiety of students who were exposed to traditional instructional methods. Thus, early grades are critical stages in controlling of math anxiety amoung young students if the instruction focuses on traditional methods of instruction . Thus, one of the concern of the present study is to investigate seventh grade students’ anxiety levels which is one of the critical levels in the development of mathematics anxiety.
Attitude towards Mathematics
Attitude, a hard to define concept, is “a learned disposition or tendency on the part of an individual to respond positively or negatively to some object, situation, concept or another person” (Aiken, 1970, p. 551). In mathematics, Ma and Kishor (1997) indicated the inconsistent research findings regarding the relationship between attitude towards mathematics and mathematics achievement. While some researchers reported a statistically significant relationship (Michelli, 2013), others stated statistically significant but not strong relationship between attitude towards mathematics and mathematics achievement (Aiken, 1970; 1976; Ma & Kishor, 1997). Ma and Xu (2004b) investigated the causal ordering between mathematics attitude and mathematics achievement of secondary school students. Students were randomly selected from seventh graders and were followed for six years until they reached 12th grade. Students completed achievement tests on basic skills, algebra, geometry, and quantitative reasoning and a questionnaire regarding attitude towards mathematics. Data analysis revealed that for all grade levels prior achievement significantly predicts future attitude. However, prior attitude does not significantly predict future achievement. Thus, researchers emphasized the predominance of achievement over attitude in secondary school years. Similarly, in a recent study, Soleymani and Rekabdar (2016) investigated the relationship between undergraduate students’ mathematics achievement and attitudes toward mathematics. They reported that previous performance has positive effect on attitude towards mathematics. However, the effect of attitude on final grade was not statistically significant. On the other hand, in their meta analytical study, Ma and Kishor (1997) stated that the effect of attitude toward mathematics on achievement was not strong and the effect of mathematics achievement on attitude toward mathematics was not significant. Thus, based on the inconsistent findings, attitude towards mathematics is chosen as one of the constructs in the present study.
Gender and School type
The role of gender in learning mathematics has been emphasized at different venues (Isiksal & Cakiroglu, 2008; Savas & Duru, 2005). Empirical studies have revealed that males are more likely to outperform females (Alacacı & Erbas, 2010; Clewell & Campbell, 2002, Soleymani & Rekabdar, 2016) especially in the area of measurement, proportionality, geometry, spatial geometry, analytic geometry, trigonometry, mathematics applications, problem solving and reasoning (Clewell & Campbell, 2002). However, research studies indicated that gender difference is also connected to the grade level and performance being measured. Females are more likely to outperform males during elementary and middle school years on computation; however, during high school, males are better at problem solving (Clewell & Campbell, 2002; Hyde, Fennema, & Lamon, 1990). Gender difference exists mostly in high school and college; but, such a difference is either weak or does not exist in elementary and middle school (Leahey & Guo, 2001; Mullis, Martin, Gonzalez, & Chrostowski, 2004). In their study with Turkish students, Alacacı and Erbas (2010) investigated the effects of gender, SES, school resources, school autonomy, school program type on mathematics performance in PISA 2006. They concluded that in Turkey the advantage of boys over girls is higher than the OECD average among 15-year-old students. Similarly, Soleymani and Rekabdar (2016) stated that male undergraduate students have better scores in mathematics performance than females. Nevertheless, research studies emphasized that the difference between males and females are getting smaller. For instance, in their study with secondary school (7-11 grades) students, Ma and Xu (2004b) stated that both males’ and females’ achievement mean scores increase in a similar manner and thus there is no gender difference among the grade levels regarding basic skills, algebra, geometry, and quantitative reasoning. Similarly, no gender difference was detected between mathematics achievement test scores of 5th graders (Michelli, 2013).
The relationship between gender and affective variables (e.g., efficacy, anxiety and attitude) in elementary years has not been explored as thoroughly as that of the relationship between gender and mathematics achievement. In addition, the findings of those studies explaining the difference in mathematics self- efficacy, mathematics anxiety and attitude towards mathematics with respect to gender were not determined as consistent as differences in achievement scores (Fennema & Sherman, 1977). For instance, the sources of gender differences in attitude towards mathematics were found to be more complex and complicated. Some studies emphasized that males showed more positive attitudes towards mathematics than females (Michelli, 2013; Tasdemir, 2009); whereas, in other studies females were found to hold more positive attitudes towards mathematics compared to their male counterparts (Savas & Duru, 2005). Similar to achievement, Ma and Xu (2004b) stated that both males’ and females’ attitude scores decrease in the same manner across grade levels indicating no gender difference regarding mathematics attitude among secondary school students. In another research, the relationship between attitude towards mathematics and mathematics achievement of 9th and 10th grade level students was examined. Researchers found out that there is a positive relationship between attitude and mathematical achievement only for females and the correlation was not significant for males (Mubeen, Saeed, & Arif, 2013).
There is no consensus regarding gender differences in mathematics anxiety. A number of studies reported females are more anxious about mathematics than males (Bonnstetter, 2007). Ma (1999) stated that gender differences in mathematics anxiety do not appear until the end of elementary grades, while this difference becomes stronger among high school and college students where female students have higher anxiety. On the other hand, some researchers reported no difference or minimal differences between mathematics anxiety levels of males and females (Birgin, Baloglu, Catlioglu, & Gurbuz, 2010). Even in a more recent study, Olmez and Ozel (2012) reported that secondary school males were significantly more anxious than females.
Regarding self-efficacy, there are number of studies investigated gender differences in mathematics self-efficacy (Pajares & Miller, 1994). Those studies reported diverse findings; for example, it was found out that 15-year old Belgian females participated in the 2003 PISA survey felt less efficacious than males (Ferla, Valcke & Cai, 2009). An analysis of TIMSS mathematics data indicated that US eight grade male students had higher mathematics self-efficacy than female students (Louis & Mistele, 2012). In their study, Isiksal and Askar (2005) examined the effect of dynamic geometry software on 7th grade students’ mathematics achievement and mathematics self-efficacy. Researchers reported no significant mean difference on gain scores of girls and boys regarding mathematics achievement and mathematics self-efficacy. In a more recent work, Kiran and Sungur (2012) studied gender difference in science self-efficacy and strategy use of middle school students. Their analyses of the data from 1932 students showed no gender difference regarding science self-efficacy and strategy use. In another recent meta-analysis of 187 studies on gender differences in academic self-efficacy (Huang, 2013), significant gender difference between -1.60 and 1.40 in terms of effect size with a mean of .08 was found out. It was observed that while females’ self-efficacy scores were significantly higher than males’ self-efficacy scores in language arts with a mean effect size of -.16, in mathematics males’ self-efficacy scores were significantly higher with a mean effect size of .18 (Huang, 2013). In a recent research, Peters (2013) reported that male college algebra students’ mathematics self-efficacy scores were significantly higher than females’ scores. Based on the literature review, it can be concluded that research studies regarding gender differences in some affective variables are inconclusive and need more attention.
Regarding the school type variable, in a study on the US NAEP data (S. Lubienski, C. Lubienski, & Crawford Crane, 2008), researchers investigated effect of school type on mathematics achievement of 4th and 8th grade students. Analysis of the large-scale NAEP data indicated that private school mathematics scores were significantly lower than scores of demographically similar public schools. NAEP findings also show that students’ own backgrounds have substantial effect on their mathematics achievement more than the school they attend (C. Lubienski & S. Lubienski, 2013). In their book, Lubienskis discuss the reasons underlying public school students’ better performance over those attending private schools (C. Lubienski & S. Lubienski, 2013). On the other hand, it was also reported in a review that schools with high SES students perform higher mathematics achievement than those with low SES students (Sellström & Bremberg, 2006). In a different research on the PISA data, the researcher compared Finnish and German students’ performance (Amermuller, 2004). Finnish students have performed better than German students in the PISA. In Germany, students are placed into different school types at early ages; yet, in Finland, there is just a single school type. Amermuller stated that German students in less prestigious school types were performing lower than those attending prestigious school types; however, there is not enough evidence showing that this low performance can be attributed to the effect of the school type (Amermuller, 2004). Thus, future research is needed to examine the effect of school type on student achievement.
Furthermore, in the accessible literature, it was seen that much more emphasis was given to the relationship between school type and mathematics achievement than the relationship between affective variables and school type. Thus, in this research study, with the data collected through nationwide standardized examination, it was aimed to investigate the relationship between school type, affective variables and mathematics achievement in the Turkish context.
Purpose
Achievement in mathematics is a gateway to prestigious jobs and future carrier choices. In addition to cognitive domains, affective domains play crucial role in performing mathematical activity. Social scientists have been interested in explaining differences in mathematics performance of students with the help of emotional parameters and self-beliefs in the last decade (Hafner, 2008). Understanding the relationship between affective and cognitive domains is essential for better academic achievement (Zan, Brown, Evans, & Hannula, 2006). Indeed, investigating and illuminating the relationship between academic performance and affective variables is important to enhance the quality of mathematics teaching and learning. However, most of the research studies conducted in Turkey and other contexts focus on the relationship between those constructs and ignore the combined effect of these constructs on achievement (Pajares & Miller, 1994). Therefore, the present study provides an alternative model consisting of three attitudinal (efficacy, anxiety and attitude) and two demographic variables (gender and school type) to study differences in mathematics performance in Turkey.
The main purpose of this study is to investigate the relationship among seventh grade students’ mathematics self-efficacy, mathematics anxiety, attitude towards mathematics, and mathematics achievements in terms of gender and school type. Another purpose is to examine the role of three affective variables (mathematics self-efficacy, mathematics anxiety and attitude towards mathematics) and two demographics (gender and school type) on predicting mathematics performance of seventh grade students in Turkey.
Research Questions
(1) Is there a significant mean difference in seventh grade students’ mathematics self-efficacy scores in terms of gender and school type?
(2) Is there a significant mean difference in seventh grade students’ mathematics anxiety scores in terms of gender and school type?
(3) Is there a significant mean difference in seventh grade students’ attitude towards mathematics scores in terms of gender and school type?
(4) Is there a significant mean difference in seventh grade students’ mathematics achievement scores in terms of gender and school type?
(5) How well do the three measures of affective variables (self-efficacy, anxiety and attitude) and two demographics (gender and school type) predict mathematics achievement of seventh grade students?
Methods
Participants
The data was collected from 934 seventh grade students with an average age of 12 from 13 elementary schools, seven public and six private, in Ankara, Turkey. The participants were selected based on the convenience of accessibility and proximity to the researcher. While 481 (51.5%) participants were from public schools, 453 (48.5 %) of them were from private schools. Regarding gender, 477 (51.1 %) female and 457 (48.9 %) male students participated in this study.
Instruments
Mathematics Self-Efficacy Scale (MSES; Umay, 2001), Mathematics Anxiety Scale (MANX; Richardson & Suinn, 1972), and Mathematics Attitude Scale (MAS; Askar, 1986) were used to collect the data.
Mathematics Self-Efficacy Scale (MSES)
The MSES (Umay, 2001) is a 5-point Likert-type scale ranging from 1 (strongly disagree) to 5 (strongly agree). The 14-item scale was developed to measure individuals’ self-efficacy beliefs in mathematics. Umay (2001) categorized the MSES items into three factors: Perception of mathematics self-esteem, awareness of behaviors in mathematics and adapting mathematics skills to daily life. “I consider that mathematics is not an appropriate profession for me”, “I know how to behave when I confront a new situation in mathematics”, and “I consider that I use mathematics effectively in daily life” are sample items for each factor, respectively. Having high scores in the MSES indicates that participants have high self-efficacy beliefs in mathematics. Umay (2001) reported a Cronbach alpha reliability coefficient of .88 for the total scale, and calculated Cronbach alpha for the present study is above .70 which is an acceptable level of reliability in educational research (Fraenkel & Wallen, 2006).
Mathematics Anxiety Scale (MANX)
The MANX was used to measure seventh grade students’ level of mathematics anxiety. It is a 5-point Likert-type scale ranging from 1 (strongly disagree) to 5 (strongly agree) and was adapted from the Mathematics Anxiety Rating Scale (Richardson and Suinn, 1972) by Erol (1989). In this scale, the participants were asked to respond to 45 items related to their level of mathematics anxiety. The items were formed under four dimensions; test anxiety, mathematics anxiety, anxiety in daily life and self-confidence in mathematics. “I am very scared of mathematics quizzes” is a sample item for test anxiety, “I am confused in mathematics courses” is a sample item for mathematics anxiety, “I am even confused of excitement while calculating the change in the bus” is a sample item for anxiety in daily life, and “I cannot even perform a simple mathematical operation such as addition while someone is watching me” is a sample item self-confidence in mathematics. Having high scores on the MANX indicated that participants feel more anxious toward mathematics-related tasks. The Cronbach alpha coefficient for the total scale was found as .91 (Erol, 1989). The Cronbach alpha for the present study is above .70, which is acceptable in educational research studies (Fraenkel & Wallen, 2006).
Mathematics Attitude Scale (MAS)
The MAS, a 5-point Likert-type scale ranging from 1 (strongly disagree) to 5 (strongly agree), was used to measure seventh grade students’ attitudes towards mathematics (Askar, 1986). The unidimensional scale consists of 20 items. “I get bored in mathematics courses” is a sample item from the MAS. Having higher scores from the MAS is an indication for positive attitudes towards mathematics. The Cronbach alpha coefficient for the total scale was .96, which is acceptable in educational research studies (Fraenkel & Wallen, 2006).
Students Level Determination Exam (SLDE)
To determine the participants’ level of mathematics achievement, their mathematics scores on the 18-item mathematics sub-test of the 7th grade Students Level Determination Exam 2010 (SLDE) was utilized. The SLDE was a nationwide standardized, valid and reliable assessment administered by the Turkish Ministry of National Education (MoNE) to select and place students into high schools. The multiple-choice test was covering the 7th grade national mathematics curriculum.
Procedures
In order to determine mathematics achievement scores of the participants, Students Level Determination Examination (SLDE) mathematics test results were obtained from schools. Schools removed students’ names from the data set. After receiving all necessary permissions from the test developers and human subject committee, at the end of the fall semester, the MSES, MARS and MAS were administered to 934 seventh grade students during their regular class hours. Researchers explained the participants that their participation was not compulsory and would not affect their grades. The students were also assured that their answers would be kept confidential. The entire process took approximately forty five minutes. Those students who were absent on the day of test administration were not included in the study; but, nothing was known about characteristics of the absent students. It should also be noted that all other participants’ data was included.
Design and data analysis
Two associational research types, causal-comparative and correlational research designs (Fraenkel & Wallen, 2006), were used in the study. The causal-comparative design was used to investigate the differences in self efficacy, anxiety, attitude and achievement scores with respect to gender and school type. To investigate main and joint effect of gender and school type on affective variables, the data were examined through two-way ANOVAs. To investigate the predicting role of mathematics self-efficacy, mathematics anxiety, attitude towards mathematics, gender and school type on mathematics performance of seventh grade students, the correlational research design was used. All predictor variables were entered into the equation simultaneously to test how well self-efficacy, anxiety, attitude, gender and school type predict the mathematics performance.
Results
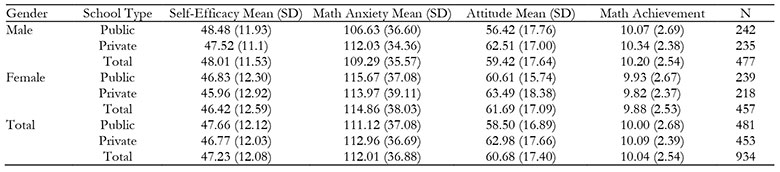
The first aim of this study is to investigate differences in seventh grade students’ mathematics self-efficacy scores, mathematics anxiety, mathematics attitude, and achievement scores in terms of gender and school type. Mean and standard deviation regarding self-efficacy scores, mathematics anxiety, mathematics attitude, and achievement scores of the participants by gender and school types are given in Table 1.
In order to test the significance of the results, two-way ANOVAs were performed. Before conducting the analysis, main assumptions, including level of measurement, independence of observations, normality and homogeneity of variance were checked. More specifically, mathematics self-efficacy, mathematics anxiety, attitudes toward mathematics, and mathematics achievement scores were measured by the scores of the participants which are continuous; hence, the level of measurement assumption was assured. In the present study, there was no interaction between participants during the data collection. Hence, it was assumed that independence of observations assumption was also assured. The skewness and kurtosis values with respect to gender and school type ranged between -.89 and .36 for self-efficacy, between - .15 and 1.02 for anxiety, between -.62 and -.26 for attitude, and between .37 and -.75 for achievement scores respectively which indicates that there was no violation of the normality assumption. In order to determine whether homogeneity of variance was ensured, Levene’s Test of Equality was examined. Results revealed that the variance within each population was equally distributed for self- efficacy ENT#091;F (3,930) = 2.469, p = .061ENT#093;, anxiety ENT#091;F (3,930) = 2.210, p = .085ENT#093;, attitude ENT#091;F (3,930) = 1.899, p = .128ENT#093;, and achievement ENT#091;F (3,930) =1.277, p =.281ENT#093;, an indication that homogeneity of variance assumption was met.
Results revealed that there was a significant main effect of gender on mean self-efficacy scores. In other words, gender had significant main effect on mean self-efficacy scores ENT#091;F(1,930) = 4.139, p = .042ENT#093; where mean self-efficacy scores of males (M = 48.01, SD = 11.53) were significantly higher than that of females (M = 46.42, SD = 12.59). Moreover, the effect size for gender (Partial eta square) was calculated as .004. According to Cohen’s criterion, the effect size of gender for the present study was relatively small. Results also revealed that school type did not have significant main effect on mean self-efficacy scores ENT#091;F(1,930) = 1.334, p = .248ENT#093; with relatively higher mean self-efficacy scores of public school students (M = 47.66, SD = 12.12) than that of private school students (M = 46.77, SD = 12.03)
The analysis for mathematics anxiety was conducted with total scores of the items to obtain a mathematics anxiety mean score for each student. As can be seen in Table 1, the mean anxiety score of students in public school students (M = 111.12, SD = 37.08) was slightly less than that of private school students (M = 112.96, SD = 36.69). In other words, results revealed that school type did not have significant main effect on anxiety scores ENT#091;F(1,930) = .588, p = .443ENT#093;. On the other hand, results revealed that gender had significant main effect on anxiety scores ENT#091;F(1,930) = 5.197, p = .023ENT#093;. This indicated that the difference between females’ mean anxiety scores (M = 114.86, SD = 38.028) and males’ mean anxiety scores (M = 109.29, SD = 35.577) was statistically significant, favoring female students. Moreover, the effect size for gender (Partial eta square) was calculated as .006, a relatively small value.
According to the mean and standard deviation of mathematics attitude, private school students (M = 62.98, SD = 17.66) were relatively higher than that of public school students (M = 58.50, SD = 16.89). Two-way ANOVA results revealed that this difference is statistically significant ENT#091;F(1, 930) = 15.830, p = .000ENT#093;. That means the attitude scores of private school students were significantly higher than the mean attitude scores of public school students. The effect size for school type was calculated as .017, a small effect size. When gender was investigated, females’ mean score was 61.69 (SD = 17.08) and that of males was 59.42 (SD = 17.636). That is, males’ average attitude score was significantly less than females’ average attitude scores ENT#091;F(1,930) = 5.260, p = .022ENT#093;. Moreover, the effect size for gender was calculated as .006. That is, the actual differences in the mean values were small which means that the difference between females and males seemed to be of little practical significance.
Students Level Determination Examination (SLDE) was analyzed in order to obtain a mathematics achievement score for each student The mean achievement score for public school student was 10.00 (SD = 2.682) and that of private school students was 10.09 (SD = 2.393). In other words, school type did not have significant effect on achievement scores ENT#091;F(1,930) = 1.301, p = .654ENT#093;, where private school students slightly scored higher than their public school counterparts. Results also revealed that there was a statistically significant main effect for gender on achievement scores ENT#091;F(1,930) = 3.992, p = .046ENT#093;. That is, the difference between achievement scores of males (M = 10.20, SD = 2.548) and females (M = 9.88, SD = 2.533) was statistically significant. Moreover, the effect size for gender was calculated as .004. That is, it was concluded that the effect size of gender for the present study was relatively small and the difference between females and males seemed to be of little practical significance.
The second aim of this study is to investigate the role of mathematics anxiety, attitude towards mathematics, mathematics self-efficacy, gender or school type on predicting mathematics performance of seventh grade students. Multiple regression analysis was performed to accomplish this aim. Before conducting the analysis, the assumptions of multiple regressions, including sample size, multicollinearity and singularity, linearity, outliers, normality, and homoscedasticity, were checked. There were five predictor variables, mathematics self-efficacy, mathematics anxiety, attitude towards mathematics, gender and school type. According to Tabachnik and Fidell (2007), the required sample size for predictor variables was should be at least 90 participants (N > 50 + 8*5). The sample of this study consisted of 934 seventh grade elementary school students which satisfies the sample size assumption. For multicollinearity and singularity assumptions, analysis revealed that bivariate correlations among predictor variables was not above .7. Hence, multicollinearity and singularity assumptions was not violated (Tabachnik & Fidell, 2007). Displayed distribution of cases’ standardized residuals in scatterplot revealed that there exist five or six extreme cases with standardized residual values above about 3.3 or less than -3.3, reflecting the outliers. However, as Tabachnik and Fidell (2007) stated few outliers in a given study could be ignored with large sample size. Thus, the outliers assumption was assured. As stated before, the distribution of self-efficacy, anxiety, attitude and achievement scores with respect to gender and school type was normal. Hence, it was concluded that the normality assumption was assured for all variables. Analyses revealed that residuals were equally distributed below and above the zero line on the scatterplot which satisfies linearity assumption of regression analysis. Displayed scatterplot of the standardized residuals revealed that the residuals plot will be roughly rectangularly distributed, with most of the scores concentrated in the center. Hence, it was assured that there was no violation of homoscedasticity assumption.
Results revealed that the linear combination of affective variables (self-efficacy, anxiety and attitude) and demographics (gender and school type) was significantly related to achievement scores ENT#091;F(5,928) = 100.295, p = .000ENT#093;. That is, the provided model consisted of affective variables and demographics significantly predicted the achievement scores. The sample multiple correlation coefficient was .592 and R2 was .351 ENT#091;F(5,928) = 100.295, p = .000ENT#093;. That is, approximately 35% of the variance of achievement scores in the sample can be accounted for by the linear combination of affective variables and demographics of interest. Correlation between variables is also given in Table 2.
As seen from Table 2, apart from the correlation between school type and achievement, self-efficacy, and anxiety, there is a significant correlation between variables. In addition, as observed in Table 3, except school type, all other variables made a statistically significant contribution to the prediction of achievement scores. From standardized beta values, it was found that self-efficacy (β = .314, p = .000), anxiety (β = -.135, p = .000), attitude (β = .224, p = .000) and gender (β = -.063, p = .021) significantly predicted achievement scores. Anxiety had negative beta values. That is, for anxiety, negative beta indicated that high anxiety scores accounted for low achievement scores. On the other hand, for gender, negative beta indicated that males’ achievement scores were higher than that of females. According to these B weights, the regression equation is as follows:
Achievement = .048efficacy ? .009anxiety+ .046attitude? .318gender + 6.604
According to Table 3, self-efficacy was recorded the highest part correlation coefficient, (Part-R = .210, p < .001), indicating that self-efficacy uniquely explains 4.5 percent of the variance in achievement scores. Moreover, anxiety had a moderate part correlation coefficient, (Part-R = -.110, p < .001), indicating a 1.2% contribution of total variance to achievement scores. Similarly, attitude scores reported the lowest part correlation coefficient, (Part-R = .144, p < .01), indicating a 2.1% contribution to total variance. Besides, gender was recorded the lowest significant part correlation coefficient, (Part-R = -.061, p < .01), meaning .4% of variance in achievement scores could be explained uniquely by this variable; yet, the school type did not make a significant contribution to total variance.
Discussion
The results revealed that there was a significant mean difference between males and females regarding their mathematics self-efficacy scores, favoring males. The fact that males outperformed females in mathematics self-efficacy beliefs was consistent with previous studies (Ferla et al., 2009; Louis & Mistele, 2012; Peters, 2013). For instance, it was found that males in high school were superior over females in mathematics self-efficacy scores (Hyde et al., 1990). This difference might be a reflection of the stereotype that males are better than females in mathematics. To state differently, Moe and Pazzaglia (2006) stated that if in a specific task gender difference is mentioned, the task can motivate students and enhance the quality of performance. Therefore, males might have felt themselves more confident in mathematics than females. On the contrary, if the superiority of opposite gender is stressed, the subject matter can demotivate students and reduce their performance. Thus, in the present study, based on the cultural factors some of the female participants might have felt inferior to males in mathematics by their parents, teachers or peers in their school and daily life. This might have influenced females’ motivation negatively for learning mathematics and decreased the amount of time and energy that they spent on mathematics. Additionally, it is possible that males’ higher mathematics performance leads to higher self-efficacy scores. Therefore, in the future, researchers should investigate how gender differences in mathematics achievement is associated with mathematics self-efficacy at different grades.
In the present study, anxiety levels of females were found to be higher than males, which was consistent with other research findings (Bonnstetter, 2007). One possible reason for this gender difference in mathematics anxiety might be biological. That is, the difference might stem from genetic sex hormones. Seeman (1997) explained, “The estrogens are neuroprotective with respect to neuronal degeneration, growth and susceptibility to toxins. The cyclic fluctuations of estrogens enhance the response to stress, which confers susceptibility to depression and anxiety” (p.1641). Another reason for the gender difference in anxiety might be psychosocial. That is, social roles in the culture and experiences might be an important factor for the gender difference in mathematics anxiety. Historically, boys are given more freedom, authority and responsibility than girls in Turkish culture. Hence, boys may not hesitate to take risks; whereas, females may take less or even none. Therefore, males feel less anxious to try when they meet a challenging task. This might be the reason of males’ lower anxiety scores in this study.
Another concern for gender difference was to investigate mean difference in seventh grade males’ and females’ attitude towards mathematics scores. Results showed that there was a significant mean difference in attitude scores of males and females. In particular, females’ attitude towards mathematics was higher than that of males. The fact that females outperformed males on attitude scores contradicts with earlier studies that reported males’ superiority in attitude scores (Asante, 2012; Michelli, 2013; Tasdemir, 2009). However, there exist some recent studies favoring females’ attitude towards mathematics in elementary years (Savas & Duru, 2005). Savas and Duru (2005) reported that females’ attitudes towards mathematics were higher than that of males and females also had a significantly more positive career interests related to mathematics than males. The source of this difference might be attributed to the large number of female mathematics teachers in Turkish classrooms. According to the Turkish Ministry of National Education (MoNE, 2013a), the number of female mathematics teachers in elementary and middle schools has been increased. When the teachers’ influence as a role model on students’ expectations, attitudes and future career plans is considered, this might enhance females’ emotional disposition toward mathematics positively. Hence, this may explain the superiority of female students’ attitudes towards mathematics in this study. In other way, gender difference regarding mathematics achievement also supports the finding concerning self-efficacy and mathematics anxiety. In other words, findings of the present study show that there was significant mean difference in mathematics achievement scores of males and females. Males outperformed females with respect to mathematics scores. The fact that males are superior in mathematics supports the findings of previous studies (Alacaci & Erbas, 2010; Clewell & Campbell, 2002; Robinson & Lubienski, 2011; Soleymani and Rekabdar, 2016; Tasdemir, 2009). This difference might stem from the sociocultural practices and stereotype effect. In particular, the stereotype that boys are better in mathematics is still alive and strong. A possible reason of this difference might be the biologically secondary mathematics abilities. Geary (1996) stated that males and females have two sets of mathematics abilities: Biologically primary and biologically secondary mathematics abilities. It was noted that biologically primary mathematics abilities were innate set of mathematics characteristics such as numeriosity, ordinality, counting and simple arithmetic which should explain why young males and females perform similarly in school mathematics. On the contrary, biologically secondary characteristics were more complex algebra and calculus skills. These skills are fostered when the learner participate and interact with the relevant sociocultural practices (Geary, 1996). Male students’ significantly higher performance over female students in the present study can be explained by Geary’s view that sociocultural practices might have enhanced the development of male students’ secondary mathematical abilities more than female students’ abilities. Moreover, the difference in mathematics achievement might stem from genetics of males and females (Kimura & Hampson, 1994). That is, in the literature, it was claimed that the left hemisphere of an individual realizes for analytical/logical thinking in both verbal and numerical operations while right hemisphere is specialized in social tasks, artistic efforts and body image (Capraro, 2001). In particular, males are more likely to use their left hemisphere (Kimura & Hampson, 1994) and hence they become more advantageous over females in mathematics (Capraro, 2001).
The findings also indicate that students’ attitude towards mathematics were differentiated in favor of private schools, while there was not a significant influence of school type on mathematics self-efficacy beliefs, mathematics anxiety and mathematics achievement. This result partially contradicts with previous studies reporting significant difference with respect to mathematics achievement between public and private schools favoring public school students (S. Lubienski, C. Lubienski, & Crawford Crane, 2008). It should be noted that the Lubienski study was conducted in the US; but, the present study was carried on with Turkish students. It is possible that Turkish private and public schools provide similar learning opportunities for students; therefore, school type differences did not exist in the Turkish context. One other possible explanation for the lack of school type effect might be the fact that the differences in affective variables and achievement regarding gender do not appear until late elementary years. To state differently, both male and female students’ emotions, feelings and beliefs about mathematics begin to shape through high school years because it was found out in a study conducted in the US that males in high school were superior over females in mathematics self-efficacy scores (Hyde et al., 1990). Therefore, in line with these views, one can conclude that students in different type of elementary schools might have similar achivement scores, expectations and beliefs towards mathematics during primary and elementary years. Hence, this might lead to similar confidentiality or fears and worry on mathematics performances of seventh grade students in both public and private schools.
The results also showed that seventh grade students’ attitudes towards mathematics were significantly different with respect to school type. In particular, private school students’ attitudes towards mathematics were higher than that of public school students. One possible reason for this difference might be the fact that private schools are commercial business enterprises; that is, to be able to enhance their market price and gain more students, emotional and academic satisfaction may be given more importance in private schools than in public schools. For this purpose, investments in technology and physical facilities have been made by private schools to enhance the quality of education and draw parents’ attention to school as well as students’. Hence, these facilities might enhance the private school students’ emotional dispositions towards mathematics more than public school students’.
The last aspect of the present study was investigating the role of personal factors (self-efficacy, anxiety and attitude) and demographics (gender and school type) on predicting mathematics achievement. The provided model significantly predicted mathematics achievements of students and each variable except school type made significant contribution to mathematics scores of students. This result is consistent with previous research supporting the influence of self-efficacy, mathematics anxiety, attitude and gender in predicting mathematics achievement (Schunk & Mullen, 2012). In addition, self-efficacy produced the highest unique contribution. This supports findings of studies that have reported that self-efficacy is one of the best predictors of achievement (Pajares & Miller, 1994). On the other hand, school type does not have significant contribution in explaining mathematics performance. The reason might be the fact that the gap between public and private schools’ level of achievement is getting smaller with the reform movements in Turkey. In fact, the Turkish Education System promotes equal educational opportunities and excellence which can balance the achievement levels of private and public schools (C. Lubienski & S. Lubienski, 2013). For instance, the nationwide mathematics curriculum highly promotes use and implementation of reform-based mathematics teaching ideas in all type of elementary schools (Koc, Isiksal, & Bulut, 2007). In addition, all students in different schools are provided with the same mathematics textbooks for free. That is, students in private and public schools have similar educational opportunities. This might be an indication of similar mathematics performances in public and private schools (C. Lubienski & S. Lubienski, 2013).
Conclusion
As discussed above, females and males differ significantly regarding their self-efficacy and mathematics anxiety scores. Females’ relatively lower self-efficacy and higher mathematics anxiety scores indicate that school curricula and other programs should be designed in a way to help improve females’ beliefs about their own competence in mathematics and diminish their level of anxiety in dealing with mathematics-related tasks. For example, adapting the cognitive level of mathematical tasks to students’ needs, interests and skills could be a viable way to help females as well as males find some value in learning mathematics and improve their self-beliefs. In Turkey, school mathematics curricula highly encourage teachers to consider individual, cultural and gender differences as assets of classroom rather than some sort of disadvantages (Koc et al., 2007; MoNE, 2013b). In fact, in the present study, females’ attitude towards mathematics was found to be more positive than males; so, it is believed that it may be relatively easier to help them improve their self- efficacy beliefs and decrease anxiety levels. Having positive attitudes may increase the likelihood of developing self-efficacy beliefs and decreasing anxiety. Lastly, in-service teacher education programs should be designed in a way to help teachers understand the fact that all students can enjoy and do mathematics. The classroom environments should promote the substantial participation of all students regardless of their gender.
In Turkey, only a small fraction of elementary and middle school schools are privately managed (MoNE, 2013a); all others are financed by public sources. Private schools are generally known as providing high quality education and supporting students’ individual and social development better than public schools; on the other hand, results of nationwide standardized assessments show that public and private schools’ performances are not much different from each other. This observation was also supported with the findings of the present study; yet, participants from private schools show a significantly higher level of positive attitude towards mathematics. Although the findings cannot be generalized to the entire country, based on the significant results, public school students’ relatively negative attitudes should be addressed at all opportunities. Knowing the fact that attitude towards mathematics at least partly predicts student involvement in mathematics and mathematics achievement, learning environments should support students’ enjoyment of mathematics.
Although the present study provided interesting findings that contribute to the literature and teaching practices, there is still more to do. Conducting comparative studies investigating both cognitive and non-cognitive constructs is necessary to better understand how various variables interact in different cultures. In the present study, we studied the Turkish context, a relatively more collectivist society; future studies can compare such collectivist social groups with more individualistic cultures. Also, it is suggested that future studies may consider interviewing some of the participants about reasons of low self- efficacy and high mathematics anxiety. Such studies may uncover some of the causes of individuals’ self-beliefs and emotions in learning mathematics. Another future research question could be if the relation among emotional variables and math performance is moderated by gender and school type.