REVISIÓN

 

Oftalmología basada en evidencias: evaluación crítica de los ensayos clínicos sobre tratamiento

Evidence based ophthalmology: critical appraisal skills on clinical trials on treatments

 

 

J.C. Mesa-Gutiérrez^a, A. Rouras-López^b, I. Cabiró-Badimón^b, V. Amías-Lamana^b y J. Porta-Monnet^a

^aDoctor en Medicina, Máster en Medicina Basada en Evidencias, FEBO (European Board of Ophthalmologists), Servicio de Oftalmología, Hospital Esperit Sant, Santa Coloma de Gramenet, Barcelona, España.
^bLicenciado en Medicina.

Dirección para correspondencia

 

 

---

RESUMEN

Objetivo: Analizar y proporcionar las herramientas para contestar a las tres preguntas que debe responder un ensayo clínico aleatorizado (ECA) sobre tratamiento: la evaluación de la validez de los resultados (o validez interna, que garantiza que los resultados del estudio no están sesgados); la importancia clínica de dichos resultados y si se pueden aplicar a pacientes individuales. Suministraremos una serie de conocimientos sencillos de estadística, diseño de investigaciones y epidemiología clínica que nos permitirán evaluar y analizar los ECA de tratamiento.
Método: Revisión de la literatura.
Resultados: Para evaluar artículos sobre tratamiento y para utilizar eficientemente un tratamiento necesitamos saber si los resultados de los ECA que los recomiendan son fiables, si tienen importancia clínica y si se pueden aplicar dichos resultados a mis pacientes.
Conclusiones: Es absolutamente fundamental comprobar que en el ensayo clínico exista una distribución aleatoria, ya que el muestreo aleatorio es imprescindible para que se cumplan los requisitos matemáticos de aplicación de las pruebas estadísticas. El seguimiento de los pacientes debe ser completo y debe medir la magnitud de los resultados y su precisión para así poder medir la eficacia del tratamiento.

Palabras clave: Aleatorización. Validez interna. Muestreo. Ocultación secuencia aleatorización. Análisis de sensibilidad. Análisis por intención de tratar. Riesgo relativo. Número necesario de tratamiento.

---

ABSTRACT

Purpose: To analyse and provide the tools to answer three questions that must be asked about a clinical trial on treatments: evaluation of validity (internal validity, so that results are not biased); clinical importance of these results and their application to individual patients. We provide simple statistics tools, clinical trial design, and clinical epidemiology for the evaluation and analysis of clinical trials on treatments.
Methods: Review of the medical literature.
Results: For the evaluation of papers on treatment and for using a treatment efficiently, we need to know if the clinical trials that support it are trustworthy, if the treatment has clinical importance and if it can be applied to my patients.
Conclusions: It is of paramount importance to check that the sample of the clinical assay has been correctly randomized, because randomization is necessary to comply with mathematical laws of application of statistical tests. Follow-up of patients must be complete in order to measure precision of results and evaluate the efficacy of treatment.

Key words: Randomization. Internal validity. Sampling. Allocation concealment. Worst case analysis. Intention to treat. Relative risk. Number needed to treat.

---

 

Introducción

La literatura médica ha de ser evaluada para valorar su nivel de evidencia, labor que realizan por nosotros las denominadas revistas secundarias, como el ACP Journal Club, la colaboración Cochrane o, más frecuentemente, nosotros mismos con la ayuda de las llamadas guías de lectura crítica. Esta labor de "evaluación", aunque pueda parecer farragosa en principio, nos permite, por un lado, conocer de forma rápida si merece la pena dedicar tiempo a un artículo y, por otro, limitar el número de artículos necesarios para mantenernos al día. Las guías de lectura crítica no son más que listas de verificación que deben cumplimentarse con los datos que obtenemos del estudio y que nos ayudarán a decidir sobre su idoneidad para responder a una pregunta clínica.

Un artículo sobre tratamiento debe responder a tres aspectos: validez de los resultados, importancia de los mismos y aplicabilidad a pacientes individuales. En esta revisión proporcionamos las herramientas para responder a estos tres puntos: la evaluación de la validez interna, que garantiza que los resultados del estudio no están sesgados; el efecto del tratamiento y su utilidad para nuestro trabajo diario.

Un ejemplo: en el último congreso de la Sociedad Española de Oftalmología, usted presencia una comunicación sobre la conveniencia de tratamiento de la hipertensión ocular mediante fármacos antihipertensivos, tras la que se establece cierta discusión. A la vuelta, y puesto que la discusión se estableció a partir de una serie de casos, decide buscar si existe una evidencia más sólida. Usted sabe que la máxima evidencia sobre la eficacia de un tratamiento se consigue mediante un ensayo clínico aleatorizado, y realiza una búsqueda bibliográfica a través de MEDLINE utilizando como palabras clave "ocular hypertension", "medical treatment" y limita la búsqueda utilizando como tipo de artículo la opción "randomized controlled trial". El resultado son 18 referencias bibliográficas entre las que se incluyen ensayos con distintos fármacos, comparaciones entre ellos y también un ensayo multicéntrico publicado en Archives of Ophthalmology¹, revista disponible en la biblioteca de su centro hospitalario.

En la tabla 1 se presenta la guía de lectura crítica que vamos a utilizar para los artículos sobre tratamiento. Pueden obtenerse guías similares en las páginas web de la red Critical Apraissal Skills Programme España (CASPe)² o del centro para la medicina basada en la evidencia de la Universidad de McMaster³.

 

Para analizar los resultados de un ensayo clínico aleatorizado (ECA), el lector debe comprender su diseño, desarrollo, análisis e interpretación. Esto sólo puede lograrse mediante una transparencia completa por parte de los autores. Varios investigadores y editores han desarrollado la declaración CONSORT (Consolidated Standards of Reporting Trials) para ayudar a los autores en el proceso de la investigación y publicación mediante unas listas de verificación y diagrama de flujos en los distintos apartados (título, resumen, introducción, material y métodos, resultados y conclusiones). La lista de verificación contiene 22 puntos cuya información es esencial para juzgar la fiabilidad o relevancia de los hallazgos. El diagrama de flujo contiene información sobre las cuatro etapas principales de un ensayo clínico (reclutamiento, intervención, seguimiento y análisis)⁴.

 

Sujetos, material y método

Realizamos una revisión bibliográfica de la información disponible que aborda el tema planteado. Al ser la Medicina Basada en Evidencias (MBE) una disciplina relativamente reciente, su sistemática de trabajo se divulga fundamentalmente en internet y por tanto, la información disponible se encuentra de forma mayoritaria, y gratuita, en la red. Así, en este trabajo casi toda la bibliografía, las hojas de cálculo y las herramientas utilizadas se han obtenido de las numerosas sites y webs disponibles en la red sobre este nuevo "estilo de proceder médico" que va arraigándose de forma progresiva en la comunidad médica.

Analizada la información, seleccionamos un ensayo clínico sobre tratamiento publicado en una revista de impacto (Archives of Ophthalmology) y procedimos a su análisis crítico a modo de ejemplo¹.

 

Resultados: ¿qué debemos pedirle a un ensayo clínico sobre tratamiento?

La pregunta necesaria para la práctica de la MBE consta como mínimo de 3 elementos y se resume en el acrónimo PICO (paciente, intervención, comparación, resultado [outcome en inglés]), y no puede responderse recurriendo a un libro de texto, sino a artículos o revisiones sistemáticas. Este tipo de preguntas son las que se nos plantean en la práctica diaria en temas que sí conocemos y con los que trabajamos habitualmente. La C del acrónimo, la "comparación", no siempre es necesaria. Una pregunta clínica bien formulada va a facilitar enormemente la búsqueda de la evidencia al permitirnos traducir fácilmente nuestros términos a palabras clave (descriptores).

Iniciemos la lectura crítica del artículo ¿Qué debemos pedirle a un artículo sobre tratamiento? Las tres preguntas genéricas a las que debemos responder son:

1. ¿Son válidos los resultados del estudio?

2. ¿Cuál es la importancia clínica de los resultados?

3. ¿Son aplicables los resultados a mis pacientes?

Análisis de la validez

Identificación de la pregunta clínica

La identificación de los elementos de la pregunta clínica nos permitirá, además de evaluar su validez interna (ausencia de sesgo), conocer su aplicabilidad, es decir, la generalización de sus resultados a nuestros pacientes, en el caso de que la muestra utilizada sea representativa. En la tabla 2 se muestran los criterios de inclusión en el estudio elegido, las intervenciones que se deben comparar y los resultados registrados, de los cuales el principal es el desarrollo de un defecto en el campo visual o la afectación de la papila.

 

La importancia de la aleatorización

La segunda cuestión, y posiblemente la más importante, es si el ensayo ha sido aleatorizado. Varias son las razones por las que es necesario que en un ensayo clínico exista una distribución aleatoria. Toda la inferencia estadística y el cálculo de probabilidades se basan en el estudio de muestras extraídas al azar. La aleatorización es el único momento del diseño experimental en el que se introducen explícitamente las leyes del azar: ellas rigen la distribución de frecuencias teóricas que vamos a comparar con las frecuencias observadas. Así pues, sólo la aleatorización da sentido real al uso de las pruebas estadísticas (buscar la "p" o el intervalo de confianza [IC] al 95%), que se utilizan para medir el poder del azar en los resultados que se están encontrando.

La segunda es que la aleatorización de muestras grandes es el único método conocido de evitar el sesgo de confusión. Si en un experimento partimos inicialmente de dos muestras comparables, y sobre una de ellas (pero no sobre la otra) realizamos una intervención, si al final aparecen diferencias entre ambas muestras podemos afirmar que la causa de las diferencias es la intervención. Si, por el contrario, en un experimento partimos inicialmente de muestras que no son comparables, después de realizar la intervención sólo en una de ellas, si al final aparecen diferencias entre ellas no podremos achacar la causalidad de esas diferencias a la intervención. Así que la comparabilidad de las muestras es un requisito imprescindible para atribuir la causalidad, para concluir que la causa de las diferencias en el resultado final es la única variable distinta entre los grupos: la intervención que se está estudiando.

A partir del teorema denominado la "Ley de grandes números" (LGN)⁵, la aleatorización de muestras grandes tiende a producir grupos uniformes en todas las variables (incluidas las desconocidas), previamente a que se aplique la intervención en estudio. A consecuencia de esta ley, el control de las variables de confusión será proporcional al tamaño muestral: el teorema funciona si el muestreo es aleatorio cuando n (tamaño muestral) es ∞. Como en nuestros ensayos clínicos nunca vamos a disponer de muestras infinitas, es imprescindible demostrar a los lectores de nuestros estudios que el efecto de la LGN para homogeneizar las muestras y controlar el efecto de los factores de confusión principales se ha cumplido para el tamaño muestral que hemos elegido. Para ello sirven las llamadas "tabla 1" de los trabajos: por consenso⁴ se ha establecido que la primera tabla de un ensayo clínico debe mostrar la frecuencia de aparición de las principales variables demográficas y/o de confusión en ambas muestras antes de que se aplique la intervención. En esta tabla no encontraremos ninguna prueba estadística para comparar ambos grupos, ninguna p que nos diga que no existen diferencias estadísticamente significativas. La p no mide la homogeneidad, aparte de que una pequeña diferencia entre dos grupos alcanzaría significación estadística si el tamaño muestral fuera lo suficientemente grande. Es el lector el que, a la vista de los resultados y aplicando su juicio, evaluará si los grupos son comparables. En la tabla 3 se muestra la "tabla 1" del ensayo que hemos elegido. Nótese el poder del azar para generar dos muestras muy similares, aunque no idénticas, como en el caso de los pacientes con antecedentes familiares de glaucoma o la asociación con miopía e hipertensión arterial, más numerosos en el grupo tratado con antihipertensivos tópicos. Usted, lector, tendrá que evaluar a partir de sus conocimientos y experiencia si esa diferencia es relevante o puede influir en el resultado.

 

¿Cómo comprobar que se ha realizado una correcta aleatorización?

El término muestra aleatoria tiene una estricta acepción matemática que difiere del que se usa popularmente. En teoría, para que una muestra sea aleatoria se requiere que cada uno de los miembros de la población que se muestrea tenga la misma probabilidad de ser seleccionado para incluirlo en la muestra: la probabilidad de asignación a los diferentes grupos es fija e igual para todos y cada uno de los individuos que participan. Este requerimiento no se cumple si la muestra se elige de manera fortuita (esto es, sin un plan específico) o de manera sistemática (números pares o impares de la historia clínica o días alternos de acudir a consulta) o conveniente (todos los que han devuelto un cuestionario contestado). Para obtener una muestra verdaderamente aleatoria de una población de pacientes se requieren maniobras especiales, como tirar una moneda insesgada, utilizar una tabla de números aleatorios o un generador computarizado de números aleatorios.

A partir de ahora hablaremos sobre aleatorización simple. Como hemos visto, la aleatorización es la parte más sensible de todo el diseño. Por ello, para dar validez a los resultados del ensayo, deberemos aprender algunos "trucos" para detectar si la aleatorización ha sido realizada correctamente. El primero, que ya hemos citado, es comprobar que el azar ha generado muestras similares o comparables cotejando los datos de la llamada "tabla 1". Pero quizá lo más curioso es saber que el muestreo aleatorio simple tiende a producir muestras homogéneas, pero de tamaños muestrales diferentes. La mayoría de la gente piensa que, por ejemplo, cuando distribuimos al azar en dos grupos (probabilidad de pertenencia a cada grupo = 0,5) un muestra total de 40 pacientes, cada una de las dos muestras resultantes debe contener 20 pacientes. Nada más lejos de la realidad, pues la teoría de probabilidades nos permite calcular, utilizando la distribución binomial (fig. 1), que la probabilidad de obtener ese resultado es del 12,54%.

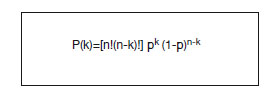
Figura 1 - Ley binomial de la probabilidad.
n: tamaño muestral total; P(k): probabilidad de obtener k sujetos.

 

Es sorprendente encontrar en la literatura el enorme número de ensayos clínicos pequeños (menos de 100 pacientes) en los que el tamaño de los grupos que se comparan es igual cuando la muestra es un número par (30/30, probabilidad de presentación = 10,3%; 40/40, probabilidad = 8,9%) o hay un desequilibrio de uno cuando la muestra total es impar (17/16, probabilidad = 13,6%; 25/26, probabilidad 11%), cuando, sin embargo, dicen en los métodos que la distribución ha sido aleatoria. El hecho de que contradigan la teoría de probabilidades hace que estos trabajos sean sospechosos de que posiblemente no se haya realizado una aleatorización real, aunque sus autores así lo afirmen.

Es tan conocido entre los matemáticos que el muestreo aleatorio tiende a producir grupos de tamaños muestrales desiguales, que los estadísticos que trabajan con muestras pequeñas suelen utilizar muestreos especiales como el muestreo por bloques permutados equilibrados. Por ello, un buen consejo para detectar que la aleatorización se ha realizado efectivamente es que, si se ha utilizado muestreo aleatorio simple, los grupos deben tener tamaño diferente. Si los grupos son iguales, se debe especificar en los métodos el sistema concreto de aleatorización que se ha utilizado (por ejemplo, bloques equilibrados).

En cualquier caso, ya hay pruebas empíricas⁶ de que el factor que más sesga los resultados, sea cuál sea el método de aleatorización utilizado, es que no se respete la ocultación de la secuencia de aleatorización (OSA). La OSA (en inglés, allocation concealment), un concepto diferente del enmascaramiento, consiste en que una vez ha entrado al estudio el primer paciente, debe ser imposible que el personal que administra la intervención adivine el grupo al que pertenecerá el próximo paciente que entre al estudio. Para que la aleatorización sea correcta debe asegurarse la OSA, y para ello los investigadores suelen utilizar varios métodos. Uno de los más utilizados es la aleatorización centralizada (vía telefónica o vía internet) en un centro coordinador diferente al resto de centros que aportan pacientes al ensayo, pero otros métodos válidos de OSA son la utilización de sobres opacos lacrados que contienen la intervención (o su etiqueta, si hay enmascaramiento, etc.) o, si se utiliza para la aleatorización el método de bloques equilibrados, cambiar el tamaño de los bloques.

Una cuestión secundaria es el diseño enmascarado respecto al tratamiento. En un estudio ideal, tanto el paciente como el clínico y el analista de los datos, desconocerían a qué grupo pertenece el paciente, pero esto no va a ser siempre posible. En el caso de terapias quirúrgicas frente a médicas es un buen ejemplo; o tratamiento médico frente a observación, como ocurre en el artículo que hemos seleccionado. En estos casos, al menos los autores habrán intentado que el analista de los resultados desconozca a qué grupo pertenecen los pacientes.

Seguimiento completo y análisis por intención de tratar

En segundo lugar, el seguimiento que se haya hecho de los pacientes deberá ser completo, es decir, que todo paciente reclutado para el estudio debe ser tenido en cuenta a su finalización, aunque en cualquier estudio van a existir pérdidas en el seguimiento. Si las pérdidas de seguimiento son excesivas, los resultados del estudio pueden ser puestos en duda, dado que es frecuente que el pronóstico de los pacientes para los que no se dispone de seguimiento sea diferente al de los demás. ¿Cómo saber si las pérdidas de un estudio invalidan el resultado? Mediante el análisis de sensibilidad (worst case analysis). Consiste en suponer que todos los pacientes perdidos en el grupo control han evolucionado bien, y todos los perdidos en el grupo tratado han evolucionado mal, y volver a calcular los resultados. Si no se modifican los resultados del estudio, las pérdidas son asumibles. En caso contrario, la fuerza de los resultados se debilita en proporción a la probabilidad que existe de que los tratados hayan evolucionado bien y los del grupo control hayan evolucionado mal.

Aplicándolo a nuestro artículo, ambas ramas del estudio presentan 84 y 89 pérdidas de seguimiento a los 78 meses (fig. 2). Para el análisis de sensibilidad supondríamos que todos los perdidos en el grupo de tratamiento han desarrollado glaucoma y que los no tratados en el grupo control no lo han desarrollado. Parece que se modifican los resultados: el riesgo de desarrollar glaucoma en la rama de tratamiento se modifica (0,05 a 0,15%) y en la rama de observación se queda en 0,11%.

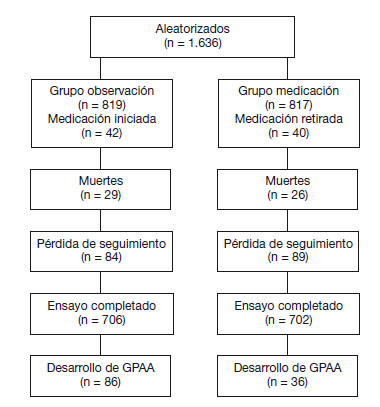
Figura 2 - Evolución de los pacientes reclutados en el ensayo clínico.
GPAA: glaucoma primario de ángulo abierto.

 

Además de las pérdidas de seguimiento, es posible que los pacientes asignados en una u otra rama no tomen su tratamiento, no sea posible aplicarlo, o incluso que haya cambios de una rama a otra. Las pérdidas también pueden deberse a efectos secundarios o a falta de eficacia del tratamiento. En cualquier caso, el paciente será analizado dentro del grupo al que fue asignado independientemente del tratamiento que haya recibido. Es lo que se conoce como análisis por intención de tratar. Aunque en principio pueda parecer que si un paciente no ha recibido el tratamiento asignado debe ser excluido del análisis en esa rama, esto no es así. En muchos estudios, los pacientes que no toman la medicación evolucionan peor, aunque tomen placebo. En el caso de pacientes con patología quirúrgica, puede que algunos no lleguen a ser operados, puede que por gravedad. Si estos pacientes se incluyen en el brazo de control, incluso una operación inútil se mostrará como efectiva, ya que todos los pacientes con peor pronóstico se han asignado al grupo control⁷.

Esta forma de análisis preserva el efecto de la aleatorización, y aproxima los resultados del estudio a la práctica clínica real. De hecho, en nuestro estudio de ejemplo, 702 de los 817 pacientes aleatorizados al grupo de tratamiento tópico lo recibieron. En los 115 restantes no fue posible su aplicación, pero se analizaron igualmente en esa rama.

Igualdad de tratamiento al margen de la intervención

Ambos grupos de estudio deben recibir la misma atención. Si se realizara un seguimiento más estricto de una de las ramas podrían detectarse determinados hechos que no "aparecerían" en la otra rama, lo que podría afectar a los resultados.

Las intervenciones distintas al tratamiento en estudio, también denominadas cointervenciones, también pueden ser un problema (por ejemplo, utilización de bloqueadores beta sistémicos como consecuencia de una cardiopatía isquémica), sobre todo si los facultativos conocen el tratamiento que están aplicando (no es un estudio a doble ciego) o se autoriza el uso de terapias muy eficaces, y distintas a las estudiadas, a criterio del médico⁸.

 

Discusión

¿Es válido el artículo que hemos elegido?

Como hemos visto, el artículo define de forma concreta pacientes del estudio mediante criterios de inclusión bien definidos, define las alternativas terapéuticas que va a comparar y el resultado que va a medir. De hecho, en la tabla 3 se presentan todas las variables que se recogen, aunque en el texto se define el evento primario como desarrollo de alteración en el campo visual o en las fotografías estereoscópicas de la papila, y quedan los restantes como secundarios.

El estudio se define como aleatorizado. Nos informan de que utilizaron un análisis por intención de tratar y una secuencia de minimización para asegurar el equilibrio en las variables y un proceso de revisión para distinguir entre los cambios en el campo visual ocasionados por el glaucoma o los originados por otras causas.

El tamaño de ambos grupos es creíble y vemos cómo el seguimiento fue casi completo, con 84 y 89 pérdidas por rama. El análisis fue por intención de tratar, manteniendo en la rama del tratamiento tópico aquellos casos en los que no se pudo aplicar. Por las características del estudio, no fue doble ciego: un total de 1.636 pacientes con hipertensión ocular y sin daño glaucomatoso fueron aleatorizados para recibir tratamiento o para observación. Sin embargo, se utilizó la técnica de enmascaramiento de observadores para determinar las alteraciones de la papila o del campo visual que fueron apareciendo durante el seguimiento. Nos consta que el analista desconoce la pertenencia a las distintas ramas de tratamiento. Se dispuso de central de aleatorización.

En definitiva, éste sí parece un artículo válido, por lo que seguiríamos con su lectura para responder a las dos siguientes cuestiones: efecto del tratamiento y utilidad para nuestro trabajo diario.

¿Tienen importancia clínica los resultados?

La importancia de los resultados se determina mediante la magnitud del efecto y la precisión del mismo. No se va a utilizar pues la significación estadística. La "famosa" p en realidad nos está indicando la probabilidad de cometer un error tipo 1 o, lo que es lo mismo, afirmar que existen diferencias entre los tratamientos cuando no las hay y únicamente las hemos encontrado por azar. Si la muestra es de gran tamaño, diferencias de mínima magnitud pueden producir diferencias estadísticamente significativas. Debe remarcarse que la diferencia estadística no tiene por qué coincidir con la diferencia clínicamente relevante. Así, podríamos encontrar que una diferencia de 3 puntos en una escala de dolor de 0 a 100 fuera estadísticamente significativa, pero no tendría ninguna importancia en la clínica diaria.

Respecto a la magnitud del efecto, en el caso de variables continuas, como el tiempo de supervivencia o la puntuación en una escala de dolor, el resultado se expresaría como diferencia de medias o de medianas (pero recuerde que diferencia clínica y diferencia estadística no tienen por qué coincidir). Sin embargo, lo más habitual es que el estudio utilice variables binarias (afectación de campo visual sí/no, afectación de la papila sí/no, muerte sí/no, recidiva tumoral sí/no, etc.). En este caso la magnitud del efecto se expresa mediante el riesgo relativo (RR), la reducción del riesgo relativo (RRR), la reducción absoluta del riesgo (RAR) y el número de pacientes a tratar (NNT). Si el artículo no ofrece estos resultados, al menos debe proporcionar los datos necesarios para su cálculo.

En el artículo que estamos utilizando como ejemplo los autores no nos proporcionan estos valores, pero los hemos calculado a partir de la tabla 3. El evento registrado es el desarrollo de glaucoma primario de ángulo abierto a los 78 meses de seguimiento, por lo que un RR inferior a 1 nos indica que el tratamiento en estudio tiene un efecto protector.

El RR del tratamiento es 0,40 o, lo que es lo mismo, el riesgo de desarrollo de glaucoma en los tratados es 0,40 veces el de los no tratados. Esta medida se entiende más fácilmente si utilizamos la RRR: el riesgo de los tratados se reduce en un 60% respecto a los controles. Si el RR fuera superior a 1 tendría un efecto perjudicial, ya que los tratados presentarían más probabilidad de desarrollo de glaucoma: un RR de 1,55 nos indicaría un riesgo superior en un 55% respecto al grupo control (tabla 4).

 

Ni el RR ni la RRR tienen en cuenta el riesgo basal de la población, cosa que sí hace la diferencia de riesgos o RAR, que nos permitirá calcular el efecto de manera absoluta. La RAR tiene la particularidad de que es pequeña cuando los riesgos en los grupos son bajos, mientras que la RRR permanece constante. Veamos un ejemplo: en la tabla 5 se muestran los resultados obtenidos con dos fármacos que se comparan contra placebo para curar una enfermedad. Se puede apreciar cómo ambos fármacos poseen el mismo RR y RRR, pero es la RAR (y en consecuencia el NNT) la que nos indica que el efecto del fármaco A es superior, ya que se aplica sobre una población con mayor riesgo basal. Esta peculiaridad es utilizada a menudo por la industria farmacéutica para promocionar sus productos, bien ofreciendo el RR o el RRR y ocultando la RAR si ésta es muy pequeña, bien ofreciendo las cifras que se obtienen en población con alto riesgo pero ofertando el producto también para población con bajo riesgo, donde el beneficio del tratamiento es a menudo desdeñable. De aquí la importancia de la declaración de los conflictos de interés.

 

En cualquier caso, la mejor medida para expresar la eficacia clínica de una medida terapéutica es el NNT, o número de pacientes a tratar con el tratamiento experimental -respecto a lo que hubiera pasado si recibieran el tratamiento control (placebo)- para evitar un evento negativo (por ejemplo, desarrollo de glaucoma) o producir uno positivo (por ejemplo, curación). Y es la mejor medida porque exactamente eso es lo que necesita saber el clínico: cuántos pacientes ha de tratar con el nuevo tratamiento para curar a uno de ellos. En el caso de que se estudien efectos adversos, se denomina número necesario para perjudicar (NNH): cuántos pacientes hay que tratar para producir un efecto indeseable. Como se muestra en la tabla 4, el NNT se obtiene a partir de la RAR.

En el estudio OHTS³ por cada 16,66 pacientes tratados con antihipertensivos se evitaría un glaucoma primario de ángulo abierto, lo que significa que el tratamiento es tremendamente ineficaz en este grupo de población. Es importante no fijarse solamente en la RRR, sino también en la RAR. Con una RAR = 25%, NNT es 4, mientras que con RAR = 0,25% el NNT es 400: habría que tratar a 400 personas para evitar que 1 se convierta de hipertensión ocular (HTO) a glaucoma. El NNT disminuye conforme la PIO aumenta.

Además, también hay que tener en cuenta que la mayoría de los tratamientos tiene efectos adversos que también se presentarán con cierta frecuencia. Para aquellos tratamientos con NNT elevados habrá que sopesar los posibles efectos adversos y el coste. Como norma general, ¡con NNT grande usar sólo si el tratamiento es barato, fácil de aplicar e inocuo¿

Lamentablemente, no podemos saber con certeza la reducción real del riesgo en los pacientes tratados. Los resultados obtenidos en la tabla 4 no son más que una estimación puntual del efecto real en la muestra seleccionada. Si tuviéramos a toda la población y no únicamente esta muestra, ¿el efecto sería el mismo? Para conocer la estimación real debemos calcular la precisión de nuestro resultado. Si es poco preciso es posible que el efecto estimado esté lejos del valor real. Esta precisión se cuantifica mediante el cálculo del IC: podemos estimar un intervalo donde se encontrará el valor real en el 95% de los casos. Este 95% se acepta por consenso. Se puede trabajar con un IC del 90 o del 99%, pero cuanto mayor sea, mayor población será necesaria para estimar un intervalo de confianza estrecho.

Una vez obtenido el IC, habrá que observar si los resultados son estadísticamente significativos. Recuerde que para el RR, el intervalo de confianza no debe incluir la unidad y para el NNT no debe incluir el 0. Si así fuera no podría sacarse ninguna conclusión útil del estudio, ya que no se habrían demostrado diferencias entre ambos tratamientos. En caso de que el NNT no incluya el 0 (existen diferencias entre los tratamientos) habrá que observar los límites del intervalo y decidir, en función de su experiencia clínica, si le parecen asumibles. Un ejemplo: en el ensayo CAPRIE⁹ de Aspirina^® contra clopidogrel para prevención de eventos isquémicos cardiovasculares y cerebrales en población de riesgo -un ensayo financiado por la industria farmacéutica- aunque la reducción del RR fue estadísticamente significativa (RRR 8,7%, p = 0,043), el NNT fue de 197, con un IC 95% entre 84 y 1.001. Esto significa que es posible que se tuviera que tratar con clopidogrel a 1.000 pacientes para curar a uno más de los que se curarían usando Aspirina^®. Si comparamos los precios de ambos fármacos (el clopidogrel es mucho más caro) no parece una decisión racional tratar a toda la población en riesgo de evento isquémico con el nuevo fármaco. El clopidogrel puede ser eficaz pero, con su precio, resulta extremadamente ineficiente.

Si el artículo no incluye el IC, éste puede obtenerse a través de la calculadora que ofrece la página web de la red CASPe¹⁰ (una sencilla página de Excel), o mediante la fórmula que ofrece la guía de la Universidad de Oxford¹¹:

IC95%RAR = RAR ± 1,96√Rc(1-Rc)/N pacientes control + Re(1-Re)/N pacientes expuestos

Con los límites superior e inferior del RAR se obtienen los límites superior e inferior del NNT.

¿Me resultarán útiles los resultados?

¿Pueden aplicarse estos resultados a mis pacientes?

Para responder a esta pregunta debemos plantearnos si nuestros pacientes, de haber estado en el estudio, habrían sido incluidos en él, aunque quizá es más sencillo hacerlo al revés y preguntarnos si existe alguna razón por la que los resultados del estudio no son aplicables a nuestros pacientes.

Una cuestión diferente es si su paciente se corresponde con un subgrupo de los incluidos en el estudio. ¿Qué hacer en ese caso? La primera cuestión es observar si los autores han realizado algún análisis de subgrupos, una situación relativamente frecuente cuando los resultados globales no muestran una clara superioridad del tratamiento en estudio y se intenta obtener mejores resultados en algún subgrupo. En muchas ocasiones estos análisis no estaban planificados al inicio del estudio, y sólo se recurre a ellos una vez obtenido el resultado global. Se pueden aceptar este tipo de análisis si se cumple alguno de los criterios siguientes¹²:

- Alta diferencia del tratamiento entre subgrupos.

- Baja probabilidad de que las diferencias se deban al azar.

- El análisis de subgrupos se había previsto como hipótesis al comenzar el estudio.

- La diferencia entre subgrupos se reproduce en otros estudios.

Sin embargo, aunque se cumplan todos los requisitos, en teoría seguiría siendo necesaria la confirmación mediante un ECA ad hoc.

¿Se tuvieron en cuenta todos los resultados clínicamente importantes?

Es importante que la variable resultado del estudio (end point) sea una variable clínicamente relevante cuya mejora justifique el uso del tratamiento. En el caso que nos ocupa se trata del desarrollo de glaucoma. Sin embargo, algunos estudios utilizan variables de valoración final indirectas (substituted end points) como podrían ser: disminución de PIO en 2-3 mmHg sin especificar el límite inferior (disminución de PIO < 24 mmHg), diferencias en el anillo retiniano "escasamente detectables" o "clínicamente significativas". Que el tratamiento mejore esos parámetros no significa que sea necesariamente beneficioso para el paciente.

El estudio también debe considerar posibles efectos nocivos del tratamiento, que permitan sopesar el riesgo de seguirlo. En el estudio que nos ocupa se consideraron también como resultados secundarios el desarrollo de síntomas sistémicos u oculares secundarios al tratamiento utilizado.

¿Compensan los beneficios del tratamiento los posibles efectos adversos y los costes?

La respuesta a esta pregunta supone valorar globalmente los beneficios/perjuicios del tratamiento en nuestro paciente, junto con otras valoraciones que en principio pueden parecer más complejas, como el coste económico del tratamiento. En este apartado será de gran valor la experiencia personal para valorar cuestiones como la dificultad para aplicar el tratamiento, bien por motivos técnicos, bien por mala adherencia al mismo por parte del paciente, o por las dificultades logísticas que pueda suponer. Si valora la introducción de un nuevo colirio antihipertensivo tendría que valorar quién costearía el tratamiento, etc., una serie de cuestiones que sólo se pueden responder desde la experiencia y el conocimiento de las particularidades de cada caso.

 

Conclusiones: hipertensión ocular y tratamiento

Aunque en principio pueda parecer farragoso, hemos visto cómo, a partir de los datos de un artículo válido y utilizando unas sencillas herramientas, es posible cuantificar el efecto de un tratamiento determinado y obtener conclusiones útiles para la clínica diaria. En nuestro caso, las conclusiones serían, en primer lugar, que no todos los individuos con PIO alta deben ser tratados. La decisión de instaurar tratamiento debe tener en cuenta muchos factores, como:

- La baja incidencia de glaucoma primario de ángulo abierto entre los individuos con HTO en los diferentes estudios de base poblacional.

- La conveniencia de un tratamiento a largo plazo: efectos adversos, coste.

- El riesgo individual de desarrollar glaucoma primario de ángulo abierto.

- La probabilidad individual de beneficio por el tratamiento.

- El estado general de salud del individuo y su esperanza de vida.

Ello justifica lo que ya nos suelen indicar las revisiones Cochrane: se precisarán estudios aleatorios de mayor tamaño y con revisiones a largo plazo para establecer la pauta y conocer el tipo de beneficio que puede conseguirse para estos pacientes, antes de establecer las indicaciones definitivas de un tratamiento caro y no exento de complicaciones.

 

Conflicto de intereses

Los autores declaran no tener ningún conflicto de intereses.

 

Bibliografía

1. Kass M, Heuer D, Higginbotham E, Johnson C, Keltner J, Miller P, et al. The Ocular Hypertension Treatment Study: a randomized trial determines that topical ocular hypotensive medication delays or prevents the onset of primary open-angle glaucoma. Arch Ophthalmol. 2002;120:701-8.        [ Links ]

2. www.redcaspe.org/herramientas/lectura/11ensayo.pdf.        [ Links ]

3. www.cche.net/usersguides/therapy.asp.        [ Links ]

4. Moher D, Schulz KF, Altman D. The CONSORT Statement: Revised Recommendations for Improving the Quality of Reports of Parallel-Group Randomized Trials. JAMA. 2001;285:1987-91.        [ Links ]

5. www.stat.berkeley.edu/~stark/Java/Html/lln.htm.        [ Links ]

6. Davidoff F, Haynes B, Sackett D, Smith R. Evidence based medicine: a new journal to help doctors identify the information they need. BMJ. 1995;310:1085-6.        [ Links ]

7. Egger M, Ebrahim S, Smith GD. Where now for meta-analysis? Int J Epidemiol. 2002;31:1-5.        [ Links ]

8. Guyatt GH, Sackett DL, Cook DJ. Users´ guides to medical literature II. How to use an article about therapy or prevention. A. Are the results of the study valid? JAMA. 1993;270:2598-601.        [ Links ]

9. CAPRIE steering committee. A randomised, blinded, trial of clopidogrel versus aspirin in patients at risk of ischaemic events. Lancet. 1996;348:1329-39.        [ Links ]

10. www.redcaspe.org/herramientas/descargas/tratamientos.xls.        [ Links ]

11. www.cebm.net/?o=1023.        [ Links ]

12. Guyatt GH, Sackett DL, Cook DJ. Users´ guides to the medical literature II. How to use an article about therapy or prevention. B. What were the results and will they help me in caring for my patients? JAMA. 1994;271:59-63.        [ Links ]

 

 

Dirección para correspondencia:
Correo electrónico: jcarlosmesa@mixmail.com
(J.C. Mesa-Gutiérrez).

Recibido el 23 de octubre de 2008
Aceptado el 25 de enero de 2010