Diseño de estudio para la correlación de los datos de reconstrucción en 3D a partir de resonancia magnética y simulación computacional tras la reconstrucción plantar en zona de apoyo

Design study for correlating data from 3D reconstruction from magnetic resonance and computational simulation after plantar bearing area surgical reconstruction

 

 

Jordán-Palomar, E.I.* y Rey-Vasalo, J.**

* Médico Adjunto, Servicio de Cirugía Plástica y Reconstructiva, Hospital Universitario Miguel Servet, Zaragoza, España.
** Médico Adjunto, Servicio de Cirugía Plástica y Reconstructiva, Complejo Hospitalario de Navarra, Pamplona.

Trabajo galardonado con el Premio Nacional de Residentes de la Sociedad Española de Cirugía Plástica, Reparadora y Estética (SECPRE) en su 47^o Congreso Nacional celebrado en Palma de Mallorca, Islas Baleares, España, Abril del 2012

Dirección para correspondencia

 

 

---

RESUMEN

La reconstrucción del pie es un tema amplio y complejo abordado frecuentemente desde el ámbito clínico, pero pocas veces desde el punto de vista de la Bioingeniería.
Este artículo muestra un método de simulación computacional mediante elementos finitos partiendo de imágenes de resonancia magnética de un pie reconstruido quirúrgicamente.
Tras la creación de los modelos en 3D del pie en diferentes momentos evolutivos y con la utilización de los datos aportados por la podobarografía estática, se realizan los cálculos que muestran las diferencias de incremento en las deformaciones ocurridas en cada uno de los tejidos implicados en la reconstrucción quirúrgica en dos momentos evolutivos diferentes, teniendo en cuenta las características de carga del paciente en cada uno de ellos. Esto permite hacernos una idea teórica del comportamiento de los tejidos participantes en una reconstrucción vistos como un material deformable.
Como resultado vemos que el volumen global de los tejidos disminuye y se adapta a los contornos, que el músculo es el tejido que más aumenta su valor relativo de deformación, y que la grasa es el tejido que mayor deformación sufre en cuanto a valores absolutos se refiere. El hueso, por sus propiedades mecánicas, apenas sufre deformaciones. La distribución de las deformaciones es compatible con la clínica y va modificándose a lo largo del tiempo.
La utilización de la Bioingeniería aplicada a la Cirugía Plástica aporta gran cantidad de información que puede usarse para la comparación tanto en el mismo paciente, como entre pacientes con diferentes características o para realizar previsiones.

Palabras clave: Microcirugía, Reconstrucción plantar, Apoyo plantar, Podobarografía, Ingeniería biomédica.

Nivel de evidencia científica 5.

---

ABSTRACT

The reconstruction of the foot is a broad and complex topic often studied from the clinical perspective, but rarely studied from the point of view of Bioengineering.
This paper shows a method of computer simulation by finite elements based on magnetic resonance imaging of a surgically reconstructed foot. After the creation of 3D models of the foot in different evolutionary stages and the use of data provided by static podobarography, the calculations show differences in the increase of deformation occurred in each of the tissues involved in reconstruction. It is made into two different evolutionary surgical times, taking into account the load characteristics of the patient in each. This allows us a theoretical idea of the behavior of tissues participating in the reconstruction as deformable material.
In results section, it´s shown that the global volume of tissue decreases and adapts to the contours, the muscle is the tissue that further increases its relative value of deformation and fat is the tissue that greater deformation suffers in terms of absolute values refer. The bone mechanical properties hardly undergoes deformations. Deformations distribution is compatible with the clinical and evolves with time over. The contact surface and the maximum pressures are similar in the theoretical model and the experimental.
The use of Bioengineering implemented to Plastic Surgery provides a great source of information that can be both used for comparison within the same patient or between different patients.

Key words: Microsurgery, Plantar reconstruction, Weight-bearing plantar foot, Paedobarography, Biomedical engineering.

Level of evidence 5.

---

 

Introducción

La reconstrucción del miembro inferior es compleja porque ha de tener en cuenta aspectos únicos como: mantener el contacto con el suelo, soportar todo el peso, permitir el máximo rango de movilidad y dar información de la posición. A su vez, el pie tiene mayores problemas que otras zonas anatómicas debido a su tendencia al edema, ateroesclerosis, vascularización distal, alta especialización de los tejidos y a la fina cobertura de las zonas de hueso. Todos ellos son factores a tener en cuenta ante una persona que requiera una reconstrucción de la zona y abren un abanico muy amplio de posibilidades quirúrgicas.

Desde los primeros artículos sobre el tema, como el de Hidalgo (1), que clasificaban las heridas según 3 categorías, hasta otros como el de Hollenberck (2) con casuísticas mucho mayores, en los que se relacionan las zonas a reconstruir con las opciones quirúrgicas más convenientes o ya centrados en la plata del pie como el de Oh (3), todos tienen una visión puramente clínica; de este modo, existen un gran número de publicaciones científicas cuyo objetivo es mostrar nuevas soluciones quirúrgicas. Los resultados de las mismas se muestran fundamentalmente mediante fotografías y radiografías, que aunque aportan una información valiosa, sólo lo hacen sobre el aspecto morfológico de la reconstrucción. En muy pocas ocasiones se ofrece información sobre los resultados funcionales, y cuando se hace no existe una estandarización de los mismos, lo que implica una dificultad para comparar entre las diferentes técnicas.

Los artículos respecto a estudios de los resultados funcionales y la recogida de los propios datos son mucho más escasos. Uno de los primeros en obtener información al respecto es el artículo de Goldberg (4) que recoge las huellas dejadas por los pies reconstruidos mojándolos en aceite y recogiendo la huella en papel secante que posteriormente se marca con rotulador. Posteriormente, Villa Moreno (5) o Meyer-Marcott (6) publican la utilidad de los registros podobarográficos tanto en la población sana como en aquellos pacientes a los que se les había realizado una reconstrucción.

En la línea de este trabajo existen otros como el de Cheung (7) que muestra el comportamiento de los tejidos mediante simulación computacional con elementos finitos, pero sobre un modelo de pie sano y no sobre un pie reconstruido quirúrgicamente, así como sobre la evolución del mismo.

El presente artículo forma parte del contenido de una Tesis Doctoral más amplia cuyo origen es un proyecto final de Master en Ingeniería Biomédica realizado en la Universidad de Zaragoza (España). Buscamos un método que permita la comparación morfológica y funcional de forma teórica y experimental de los resultados de las deformaciones, así como de la comparativa de la presión media y superficie de contacto en cada uno de los tejidos implicados en la reconstrucción quirúrgica del pie en momentos evolutivos correspondientes a los 3 y a los 9 meses de postoperatorio.

 

Material y Método

Para este modelo se partió del caso de una paciente que sufrió un accidente de moto que implicó la pérdida total de la zona plantar media y posterior. Se realizó un colgajo libre de dorsal ancho con paleta cutánea para la zona de apoyo e injertos de piel parcial en la zona dorsal (Fig. 1).

 

 

Una vez realizada la reconstrucción quirúrgica y pasado un tiempo suficiente para que la paciente se pudiera poner de pie, se realizaron las pruebas pertinentes: resonancia magnética (RM), podobarografía estática y dinámica. Las pruebas de carga para obtener las huellas con las presiones reales de la paciente se realizaron con el sistema para el registro y análisis de distribución de presiones FottWork^® en las instalaciones de la empresa Podoactiva (Huesca, España) coincidiendo con la toma de las imágenes de RM, con el objetivo de correlacionar los resultados obtenidos en ambas. Los parámetros registrados en posición estática (bipedestación durante 4 segundos) (Fig. 2) son: presión media (kPa), presión máxima (kPa), superficie total (cm²), tiempo de carga (%), distancia al centro de equilibrio (cm.) y superficie centro de equilibrio (cm²).

 

Como prueba de imagen eligimos la RM ya que lo que nos interesa analizar son los tejidos blandos, tanto los remanentes en el pie como los transferidos desde la espalda. Se realizan cortes coronales, sagitales y longitudinales potenciados en T1 y T2 para poder comparar los tejidos ricos en agua (T1) y los ricos en grasa (T2) de forma independiente. Estos registros se realizaron en las instalaciones del Complejo Hospitalario de Navarra (Pamplona, España).

Los archivos DICOM de la RM se importan al programa Mimics^® , donde se realiza la identificación de los tejidos basada en la escala de grises correspondiente a cada uno (Fig. 3). Posteriormente se comprueba la corrección en la diferenciación de cada uno. Se generan 5 tejidos diferentes: hueso, conectivo (se denomina al remanente de partes blandas propias del pie tras el desbridamiento), músculo (dorsal ancho), grasa (paleta cutánea dorsal ancho) y piel (paleta cutánea dorsal ancho, injertos y piel propia del pie) (Fig. 4).

 

 

Una vez obtenidos estos volúmenes compactos, se importan a Harpoon^® donde se transforman en una malla de elementos finitos compuesta por tetraedros, en los que donde cada uno de ellos posee 4 nodos. El análisis mecánico de la reconstrucción virtual del pie permite calcular e interrelacionar la deformación de cada uno de los tetraedros que componen los tejidos (Fig. 5). Con esto conseguimos que cada uno de los volúmenes correspondientes a cada uno de los tejidos modelados se comporte como un bloque homogéneo pero flexible, tal y como ocurre en la realidad.

 

 

Cuando se tienen las mallas correspondientes a cada uno de los tejidos, debemos definir su comportamiento mecánico. De forma experimental sabemos que, por ejemplo el hueso, es un material mucho más duro y menos deformable que la piel. Estas características están determinadas por las propiedades mecánicas de cada uno de ellos. Existen numerosas publicaciones al respecto del comportamiento de los tejidos que componen el pie (7-13). Los tejidos constituyentes del pie son en su mayor parte blandos y su comportamiento es fuertemente no lineal, por lo que para simularlo correctamente es necesario implementar modelos hiperelásticos como son el modelo de Ogden o el polinomial. Finalmente, se decidió considerara el hueso como material elástico lineal y el resto de tejidos hiperelásticos cuasi incompresibles (Tabla I). Tanto el tejido conectivo como el músculo se simularon como materiales hiperelásticos por medio de una función de densidad de energía de deformación de segundo orden, cuyos parámetros se definen en la Tabla I.

 

 

La grasa también se consideró hiperelástica y su densidad de energía de deformación se simuló por medio de un modelo Ogden de primer orden.

A continuación explicamos con mayor detalle los modelos de comportamiento para cada tejido, incluyendo las fórmulas necesarias para calcular los parámetros.

Hueso

Tiene un comportamiento de material elástico lineal. Los detalles de sus propiedades son los que se citan en la Tabla II.

 

 

Conectivo

Se comporta como un material hiperelástico. El modelo que va a seguir es el polinomial con segundo orden n=2. El modelo hiperelástico se utiliza para representar la naturaleza no lineal y casi incompresible de los tejidos blandos. Un modelo polinomial de segundo orden se adopta con la forma:

donde U es la densidad de energía de deformación por unidad de volumen; ij C y D son parámetros de los materiales; e son el primer y segundo invariantes de las deformaciones y se definen como:

donde y son la relación de volumen y las deformaciones principales, respectivamente. Los valores de los coeficientes para el tejido blando encapsulado utilizados en este artículo fueron calculados por Cheung en Abaqus^® , basándose en datos de curvas tensión-deformación uniaxial (7).

Músculo

Se comporta como un material hiperelástico y además sigue el modelo polinomial de segundo orden. Las características son las mismas que hemos citado para el tejido conectivo.

Grasa

Tiene un comportamiento hiperelástico y el modelo que se ha utilizado es Ogden (n=1). Este modelo se usa para representar las propiedades de los materiales no lineares de la piel y la almohadilla de grasa. El modelo Ogden de primer orden describe la energía de deformación (U) con la forma:

donde λ1-3 son los alargamientos y µ (en unidades de tensión) y a (adimensional).

Piel

Por último, para la piel existen modelos de comportamiento evolutivo de la curación de heridas donde la piel se modela como un material viscoelástico (8,9) que nos dan una aproximación de la deformación. Sin embargo, en otros trabajos (7, 10) el comportamiento de la piel se consideró como un material hiperelástico. No obstante, el artículo de Delalleau (12) se encontró que no es adecuado para el modelado de la piel humana.

En nuestro trabajo, simularemos la piel suponiendo un comportamiento hiperelástico y su función densidad de energía de deformación se simulará por medio de una función de Ogden de segundo orden (n=2), que es más adecuada para el modelado de la piel, y la función de la energía tiene la forma:

donde U es la energía de deformación por unidad de

volumen, µ i, a i y D son parámetros del material, y λ1, λ2, y λ3 son las tensiones principales. Una vez determinados los parámetros de los comportamientos de los materiales se determinan las condiciones de contorno, es decir, las peculiaridades de este modelo en concreto. En este caso vamos a determinar: superficie maestra, superficie esclava y por último la zona de carga. La simulación computacional mediante elementos finitos se realiza con el software Abaqus^®.

Superficie maestra

Se crea una superficie contra la cual tendrá lugar el contacto del pie reconstruido en 3D, que sería el equivalente a la superficie de la plataforma de presiones. Se considera como mucho más rígida que los tejidos del pie, por lo que se define como superficie maestra. Se impide el movimiento de la superficie maestra en cualquiera de los ejes.

Superficie esclava

Se define como la parte externa de la piel plantar. Es una superficie que se encuentra en la zona central de la planta del pie, imaginando la huella que dejaría la paciente al pisar. Las superficies esclava y maestra se muestran en la Figura 6.

 

 

Área de carga

Para simular el contacto del pie con la plataforma de presiones, la carga de la parte superior del cuerpo se aplica sobre la parte superior del corte de tibia y peroné en el modelo tridimensional. Así pues, para simular las condiciones de carga sobre el pie, se toma el peso de la paciente y se distribuye de forma que reproduzca fielmente el reparto que se produce en la realidad (Fig. 7).

 

 

Se observa clínicamente que la paciente no apoya igual en cada uno de los momentos registrados, debido principalmente al dolor y a la inestabilidad que compensa apoyando menos peso sobre el pie reconstruido. Estos factores se deben tener en cuenta a la hora de realizar la simulación. Considerando que la presión media es igual a la carga total ejercida dividida entre la superficie, y con los datos obtenidos experimentalmente mediante podobarografía estática referentes a la presión media y a la superficie total de la huella del pie en cada momento, podemos calcular la carga soportada por dicho pie en cada registro, siendo de 11,8kp en febrero de 2010 y de 45,5kp en septiembre de 2010, y con estos valores, realizar los cálculos de la simulación computacional.

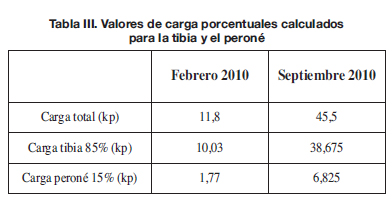
La carga llega al pie a través de la tibia y del peroné; para decidir el porcentaje que debe colocarse en cada uno se realizaron una serie de pruebas. Tras comprobar la poca influencia que tiene la diferencia de reparto de cargas entre tibia y peroné, los siguientes ensayos se llevaron a cabo asumiendo el reparto tibia 85% , peroné 15% (Tabla III).

 

 

Resultados

Una vez realizada la malla tridimensional de cada uno de los tejidos del pie y definidos todos los comportamientos, se realiza la simulación computacional mediante elementos finitos con el software Abaqus^®, con el objetivo de definir cuáles son las deformaciones producidas en cada uno de los tejidos en los dos diferentes momentos evolutivos de la paciente correspondientes a febrero de 2010 (3 meses de postopratorio) y septiembre de 2010 (9 meses de postoperatorio). Se simula el momento en que la paciente se encuentra de pie sobre la plataforma de carga, validando el modelo mediante la comparación de los resultados de las presiones de contacto obtenidas en la simulación con las mediciones reales obtenidas mediante podobarografía. Posteriormente se analizan las solicitaciones mecánicas de los tejidos del pie con el fin de determinar el modo de trabajo de los mismos tras la intervención quirúrgica. A continuación, se realiza una valoración tejido por tejido.

Hueso

La carga se realiza por los nodos que se encuentran repartidos sobre la superficie superior del corte de tibia y peroné con la proporción: tibia 85% , peroné 15% . Si se observa detenidamente la Figura 8, vemos que el hueso al ser un material sólido rígido y que la carga es pequeña en febrero de 2010 se producen cambios del orden de microdeformaciones con valores máximos de deformación próximos a 0,0005 (500 µe). Los valores máximos alcanzados en septiembre de 2010 están alrededor de 0,0013 (1300 µe), siendo la zona de los metatarsianos la más sobrecargada y aumentando ésta en los dedos 4^o y 5^o.

 

 

Músculo

La carga se realiza por trasmisión desde el hueso. Debe tenerse en cuenta que el resto de tejidos son más blandos, pero con gran contenido en agua, lo que los hace más incompresibles.

Si se observa la Figura 9 vemos que, en ambas, apenas se producen deformaciones en la zona dorsal del pie, lo cual concuerda con lo esperable clínicamente, es decir que el músculo resulta comprimido en su parte inferior entre el hueso y la zona plantar. Respecto a los valores máximos, en febrero de 2010 se alcanzan cifras de 0,1500 y en septiembre de 2010 los valores son de 0,4217. Si nos fijamos en la distribución, vemos que en febrero de 2010 la sobrecarga se realiza en la parte anterior del colgajo muscular, que se corresponde con la zona central del pie, lo que concuerda con lo observado clínicamente. Sin embargo, en septiembre de 2010 las deformaciones se distribuyen más ampliamente a lo largo de toda la planta del pie.

 

 

Si nos fijamos en la morfología en sí misma, también se puede diferenciar la progresiva disminución del volumen tanto en la zona dorsal como plantar, así como una mejor adaptación al contorno del dorso del pie en septiembre de 2010.

Grasa

La grasa tiene una evolución en su comportamiento similar a la del músculo, ya que va aumentando su su perficie en la zona plantar y también aumenta sus valores de deformación.

Si se observa la Figura 10, vemos un adelgazamiento de la grasa en septiembre de 2010 con respecto a febrero de 2010 por su mayor deformación tras la aplicación de la carga. Tomando los valores de febrero de 2010 con deformaciones máximas de 0,400 y en septiembre de 2010 de 0,5500, vemos que la grasa sufre las mayores deformaciones de todos los tejidos estudiados, teniendo sus picos en la zona correspondiente al apoyo del calcáneo.

 

 

Piel

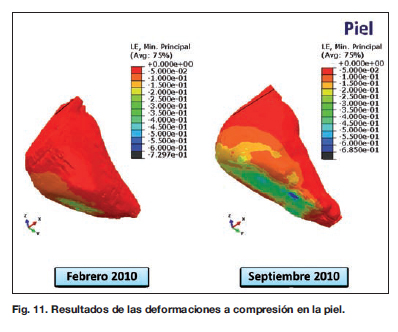
La carga se realiza por trasmisión desde el resto de los tejidos con los que entra en contacto. Al igual que con el músculo, observamos que en la zona dorsal del pie se producen menos deformaciones que en la zona plantar, que es lo que cabría esperar también clínicamente (Fig. 11).

 

 

Si nos fijamos en los valores de las deformaciones máximas, podemos ver que en febrero de 2010 los valores se aproximan a los 0,2500 y en septiembre de 2010 son de 0,6000. Si vemos la distribución espacial de las mismas, hay una zona próxima a la cabeza del 5^o metatarsiano que está sometida a mayores deformaciones.

De forma esquemática se muestra en la Tabla IV una comparación con los valores máximos de las deformaciones en cada uno de los tejidos. De entre todos ellos, el músculo es el que experimenta un mayor incremento de las deformaciones máximas y la grasa es la que experimenta una mayor deformación en cuanto a términos de valor absoluto se refiere.

 

 

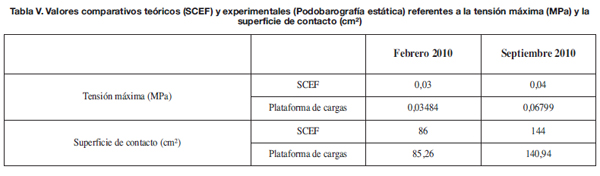
Por último, si vemos en la Tabla V los valores comparativos teóricos (simulación computacional mediante elementos finitos, SCEF) y experimentales (podobarografía estática) referentes a la tensión máxima (MPa) y la superficie de contacto (cm²), se observa que ambos se encuentran próximos.

 

 

Discusión

Visto lo expuesto en el artículo de forma global, nos enfrentamos a dos problemas, uno quirúrgico acerca de cómo conseguir una reconstrucción lo más anatómicamente parecida al pie sano y otro mecánico acerca de cómo compensar todos los equilibrios de presiones, superficies de contacto, tiempos, porcentajes de carga, etc., presentes al caminar en una persona sana.

La biomecánica de la marcha ha sido ampliamente estudiada en población sana (5) y las aplicaciones de las plataformas dinamométricas pueden aportarnos mucha información al respecto (17). Los estudios realizados en población enferma suelen estar relacionados con patología neurológica o con úlceras diabéticas. Son pocos los que evalúan estos parámetros en pacientes postquirúrgicos (18). Los estudios de Meyer-Marcott (6) utilizan la podobarografía postoperatoria agrupando los pacientes según si la zona reconstruida se encuentra en zona de apoyo o de no apoyo y realizando una comparativa de los valores de presión máxima y media.

Desde el punto de vista quirúrgico se pueden dar muchas opciones para resolver un problema de similares características, tal y como reflejan numerosos artículos al respecto (1-4, 15,16). En nuestro caso se optó por un colgajo libre con isla cutánea para la zona de apoyo. El resultado clínico fue bueno, y aunque existen partidarios y detractores de este tipo de reconstrucciones, éste no es el objetivo del presente artículo.

Planteamos el problema analizándolo tanto desde el punto de vista de la Cirugía Plástica como considerándolo un problema puramente mecánico basado en la forma, las propiedades y el comportamiento de los tejidos como materiales en sí mismos. Esto hace que el pie sea procesado con los mismos métodos que se utilizan en ingeniería para evaluar prototipos mecánicos o estructurales de forma teórica antes de pasar a producción real.

Cuando se trabaja con tejidos blandos debemos tener en cuenta que se deben utilizar modelos de grandes deformaciones, esto quiere decir que los materiales se van a deformar previsiblemente por encima del 5%.

Con el diseño de modelos teóricos mediante simulación computacional por elementos finitos unido a la podobarográfía, se muestra el comportamiento de los tejidos participantes en una reconstrucción quirúrgica compleja. Estos modelos no son algo frecuente en la práctica clínica y del mismo modo no existe demasiada bibliografía al respecto.

Para realizar la simulación computacional mediante elementos finitos existen numerosas publicaciones. Gu(14) realiza la simulación computacional de la distribución de las cargas en el hueso en modelo de elementos finitos es hueso sano con configuración normal; Javierre (8) plantea un modelo mecano-químico de la contracción de heridas; Manoussaki (9) muestra un modelado mecano-químico de la vasculogenesis y la angiogénesis; Valero (19) plantea la influencia de la orientación de las herida respeto a los ejes cutáneos. En cuanto a los estudios sobre las propiedades mecánicas de los tejidos, la mayoría son descriptivos y están realizados en muestra de población sana, como el de Nava (13), que recoge las propiedades del tejido mediante aspiración del mismo. Otros como Boyer (20) lo hacen mediante microindentación. Pero debemos tener en cuenta que los tejidos, como ya sabemos desde hace tiempo de forma experimental, no tienen las mismas características in vivo que in vitro. También que aún cuando se comparan in vivo, la orientación de las fibras de colágeno según las líneas de Langer hace que la piel tenga un comportamiento anisótropo (12). Esto nos lleva a tener que considerar estas propiedades no lineales de los tejidos durante la simulación. Con todo ello se intenta hallar modelos y parámetros que ya hayan sido implementados anteriormente con éxito. Al tratarse de tejidos biológicos existe cierta variabilidad entre los datos utilizados dependiendo de la publicación, ya que las propiedades de estos tejidos varían según la ubicación ensayada y entre individuos. La mayor parte de investigaciones que podríamos considerar semejantes a ésta se centran en el estudio de pies estructuralmente sanos, pertenecientes a pacientes sanos o con alteraciones debidas a enfermedades como la diabetes. Otros utilizan tejido proveniente de cadáveres. Es difícil realizar una comparación cercana con otros estudios similares.

Los resultados obtenidos son compatibles con lo observado clínicamente, pero de este modo, al menos de forma teórica, pueden ser cuantificados y observados de forma independiente en cada uno de los tejidos participantes de la reconstrucción.

Al utilizar de forma paralela los resultados obtenidos de forma teórica (SCEF) con los obtenidos de forma experimental en la plataforma de cargas, podemos comparar ambos y extrapolar dichos resultados obtenidos en uno y otro ganando gran cantidad de información para la clínica. Como ya hemos dicho al inicio, el contenido de este artículo forma parte de una Tesis Doctoral más amplia, que todavía tiene resultados pendientes y que serán objeto de nuevas publicaciones.

 

Conclusiones

Los datos sobre el análisis biomecánico del comportamiento del pie presentados en este artículo son teóricos y basados en una lógica clínica, ya que no existe en este momento la forma de comprobar de forma experimental y precisa los valores en el interior de cada uno de los tejidos. Sí es posible medirlos en la superficie cutánea, que es precisamente el punto de partida de todo el estudio que realizamos.

La Cirugía Plástica y la Bioingeniería no son campos tan alejados como pudiese parecer y ambos pueden beneficiarse el uno del otro. Introducir la utilización de nuevos sistemas de evaluación es complicado en la práctica habitual, pero una vez conseguidos y ajustados, nos aportan gran cantidad de información.

 

Agradecimientos

Al Complejo Hospitalario de Navarra (Pamplona, España) donde se han realizado las cirugías. Al Departamento de Ingeniería Mecánica de la Universidad de Zaragoza (Zaragoza, España), M^o José, Etel, Marta y Gabriel por su colaboración. A Podoactiva, empresa colaboradora dedicada a la Biomecánica y a su director Victor Alfaro, por todo su interés.

 

Declaración

Ministerio de Ciencia e Innovación, a través del Proyecto DPI 2009-07514 enfocado al modelado computacional de la cicatrización de heridas acoplado a factores bioquímicos y biomecánicos.

 

Bibliografía

1. Hidalgo, D. A., and Shaw, W. W.: Anatomic basis of plantar flap design. Plast. Reconstr. Surg. 1986; 78: 627- 636.         [ Links ]

2. Hollenbeck, S., Woo, S., Komatsu, I., Erdmann, D., Zenn, M., Levin, S.: Longitudinal Outcomes and Application of the Subunit Principle to 165 Foot and Ankle Free Tissue Transfer. J Plast Reconstr Aesthet Surg. 2010; 125: 924-934.         [ Links ]

3. Oh, S.J., Moon, M., Cha, J., Koh, S.H., Chung, C.H.: Weight-bearing plantar reconstruction using versatile medial plantar sensate flap. J Plast Reconstr Aesthet Surg, 2011; 64:248-254.         [ Links ]

4. Goldberg, J.A., Adkins, P., Tsai, T.M.: Microvascular reconstruction of the foot: weight-bearing patterns, gait analysis, and long-term follow-up. Plast Reconstr Surg., 1993; 92(5):904-911.         [ Links ]

5. Villa Moreno, A., Gutiérrez Gutiérrez, E., Pérez Moreno, J.C.: Consideraciones para el análisis de la marcha humana. Técnicas de videogrametría, electromiografía y dinamometría. Revista Ingeniería Biomédica. 2008; 3:16-26.         [ Links ]

6. Meyer-Marcott, M.V., Sutmoeller, K., Kopp, J., Vogt, P.M.: Postoperative insole-paedobarographic gait analysis for patients with flap coverages of weight-bearing and non-weight-bearing areas of the foot. J Plast Reconstr Aesthet Surg., 2011; 29: 1-7.         [ Links ]

7. Cheung, J.T., Zang, M., Leung, A.k., Fan, Y.: Three-dimensional finite element analysis of the foot during standing- a material sensitivity study. Journal of Biomechanics, 2005: 1045-1054.         [ Links ]

8. Javierre, E., Moreo, P., Doblaré, M., García-Aznar, J.M.: Numerical modeling of a mechano-chemical theory for wound contraction analysis. Int J Solids Struct, 2009: 3597-3606.         [ Links ]

9. Manoussaki, D.: A mechanochemical model of angiogenesis and vasculogenesis. ESAIM-Math Model Numer. Anal Model Math Ana., 2003: 581-599.         [ Links ]

10. Linder-Ganz, E., Shabshin, N., Itzchak, Y., Yizhar, Z., Siev-Ner, I., Gefen, A.: Strains and stresses in sub-dermal tissues of the buttocks are greater in paraplegics than in healthy during sitting. Journal of Biomechanics, 2008: 567-580.         [ Links ]

11. Burstein, A.H., Reilly D.T., Martens, M.: Aging of bone tissue: mechanical properties. J Bone Joint Surg Am. 1976; 58: 82-86.         [ Links ]

12. Delalleau, A., Josse, G., Lagarde, J.M., Zahouani, H., Bergheau, J.M.: A nonlinear elastic behavior to identify the mechanical parameters of human skin in vivo. Skin research and Technology. 2008: 152-164.         [ Links ]

13. Nava, A., Mazza, E., Kleinermann, F., Avis,N.J., McClure, J.: Determination of the Mechanical Properties of Soft Human Tissues through Aspiration Experiments. Swiss NSF Computer Aided and Image Guided Medical Interventions (NCCR CO-ME) project, 2003.         [ Links ]

14. Gu, Y.D., Ren, X.J., Li, J.S., Lake, M.J., Zhang, Q.Y., Zeng, Y.J.: Computer simulation of stress distribution in the metatarsals at different inversion landing angles using the finite element method. International Orthopaedics, 2010: 669-676.         [ Links ]

15. Lineaweaver, W. C.: Skin graft coverage of critical marginal wounds in microsurgical cases. Microsurgery. 2013; 33:315-317.         [ Links ]

16. Selmanpakoglu, N., Güler, M., Sengezer, M., Türegün, M., Isik, S., and Demirogullari, M.: Reconstruction of foot defects due to mine explosion using muscle flaps. Microsurgery. 1998, 18:182-188.         [ Links ]

17. Collado Vázquez, S.: Plataformas dinamométricas. Aplicaciones. Revista de la facultad de ciencias de la salud, Universidad Alfonso X el Sabio. 2005; 3.         [ Links ]

18. Tang, S.F., Chen, C.P., Hong, W.H., Chen, H.T., Chu, N.K., Leong, C.P.: Improvement of gait by using orthotic insoles in patients with heel injury who received reconstructive flap operations. Am J Phys Med Rehabil, 2003; 82:350-356.         [ Links ]

19. Valero, C., Javierre, E., Garcïa-Aznar, J.M., Gómez- Benito, M.J., Menzelc, A.: Modeling anisotropic wound healing: effect of the relative position of wounds with respect to collagen fibers orientation. Journal of the Mechanics and Physics of Solids. 2014; 00: 1-12.         [ Links ]

20. Boyer, G., Zahouani, H., Le, B.A., Laquieze, L.: In vivo characterization of viscoelastic properties of human skin using dynamic micro-indentation. 2007 Annual International Conference of the Ieee Engineering in Medicine and Biology Society, 2007; 1-16: 4584-4587.         [ Links ]

 

 

Dirección para correspondencia:
Dra. Elena Irene Jordán Palomar
C/ Borja n^o 9, 1^oC.0
50017 Zaragoza, España.
e-mail: dra.jordan.cirplastica@gmail.com