INTRODUCCIÓN

La insuficiencia cardiaca (IC) es un importante problema de salud pública, por su creciente prevalencia, su elevada mortalidad, el significativo consumo de recursos sanitarios y el importante impacto sobre los pacientes y sus familias en términos de deterioro de calidad de vida y estado funcional¹.

Aunque la incidencia de la IC no haya aumentado, tanto al envejecimiento progresivo de la población como la mayor supervivencia de los pacientes tras un infarto de miocardio y el mejor control de los factores de riesgo cardiovascular (FRCV) (hipertensión arterial, diabetes) han producido un aumento progresivo de su prevalencia. Al contrario de lo que sucede con el conjunto de las enfermedades cardiovasculares, la mortalidad por IC se mantiene estable. Según los datos publicados en el Instituto Nacional de Estadística (INE), la IC es la cuarta causa de mortalidad en España con 18.453 (4,6%) muertes en el año 2012².

La IC representa el 2,5% del gasto sanitario, debido al elevado consumo de servicios, en forma de hospitalizaciones, visitas, pruebas diagnósticas, derivaciones y polifarmacia³. Es importante destacar que los costes aumentan con los reingresos así como en las fases más avanzadas de la enfermedad. Un momento clave en la evolución de la IC es cuando se produce una hospitalización: la descompensación que conlleva un ingreso hospitalario representa un incremento del riesgo de muerte⁴ así como un alto riesgo subsiguiente de reingresos⁵ (del 25% al 40% de los pacientes serán readmitidos dentro de los siguientes 60-90 días).

Los pacientes que ingresan son un subgrupo con peor pronóstico y, por lo tanto, susceptibles de recibir un seguimiento específico. Identificarlos es un paso clave para la mejora de la calidad asistencial en IC⁶. Este reto todavía está pendiente de resolver, ya que el número de rehospitalizaciones no se ha reducido⁷. La elevada mortalidad y alto número de reingresos reflejan también que el pronóstico de la IC sigue siendo sombrío y los avances conceptuales en su tratamiento parecen estancados, como indica el número de ensayos clínicos recientes sin resultados favorables⁸.

El estudio de las hospitalizaciones por IC presenta también una dificultad metodológica. Cuando tenemos una variable dependiente con datos de conteo no negativos (en nuestro caso “número de hospitalizaciones de los pacientes”. Y=0, 1,...) generalmente se modela con regresión de Poisson. Sin embargo, los modelos de Poisson presentan problemas en dos situaciones⁹: cuando existe sobredispersión, porque la varianza sea mayor que la media, y cuando los datos tienen una frecuencia elevada de ceros. Algunos de los modelos que se han propuesto para superar las limitaciones de los modelos de regresión de Poisson son binomial negativa (BN), Poisson inflado de ceros (ZIP), binominal negativa inflada de ceros (ZINB), Poisson de Hurdle y BN de Hurdle¹⁰.

La diferencia entre los modelos Hurdle y los modelos inflados de ceros es que estos últimos se interesan por descubrir los orígenes de los ceros observados, es decir, consideran la posibilidad de la existencia de ceros auténticos y ceros falsos. En un modelo Hurdle se asume que hay dos tipos de observaciones, las que nunca experimentan un acontecimiento y las que siempre tienen al menos un evento. Por el contrario, en un modelo inflado de ceros se suponen dos grupos, uno caracterizado por no experimentar nunca un acontecimiento y un segundo grupo en el que los pacientes podrían experimentar o no un evento con una determinada probabilidad. La principal limitación de estos modelos es la necesidad de contar como mínimo con algún cero, lo cual provoca realizar inferencia de forma independiente en cada distribución¹¹.

El objetivo de este trabajo fue comparar varios métodos para modelizar la variable hospitalizaciones y determinar el efecto de los factores asociados con los ingresos hospitalarios en casos incidentes de IC.

MATERIAL Y MÉTODOS

Se realizó un estudio de cohortes retrospectivo multicéntrico. El periodo de seguimiento comprendió desde el 1 de enero de 2006 hasta el 31 de diciembre de 2010. El ámbito de estudio fue la población cuyo hospital de referencia era el Hospital Clínico San Carlos de Madrid, que incluía 22 zonas básicas de salud urbanas situadas en los distritos de Centro, Chamberí y Latina, con una población adscrita de 525.000 personas.

La población de estudio la constituyeron sujetos con tarjeta sanitaria individual (TSI) e historia clínica abierta, mayores de 24 años, con al menos 1 consulta registrada en atención primaria (AP) durante el año 2006. La información se extrajo de la historia clínica electrónica de AP (OMI-AP). Se definió como caso el registro del diagnóstico de IC (códigos K77 y K82 de la Clasificación Internacional de AP 1⁴) realizado por el personal médico de AP en la historia clínica electrónica a partir del 1 de enero de 2006.

Como variables sociodemográficas se registraron la edad, sexo, tipo de usuario (activo o pensionista) y el nivel de renta, asignando a cada paciente la de su centro. Para ello se imputó a cada centro de salud la Renta Bruta Disponible (RBD) per cápita territorializada del año 2000, elaborada por el Instituto de Estadística de la Comunidad de Madrid. Como variables clínicas se recogieron la presencia de factores de riesgo cardiovascular (FRCV) y comorbilidades asociadas (valvulopatías, hipertensión arterial, cardiopatía isquémica, accidente cerebrovascular, arritmias, diabetes, obesidad o sobrepeso y trastorno del metabolismo lipídico), la administración de la vacuna antigripal y el tratamiento farmacológico registrado en el OMI-AP (antitrombóticos, betabloqueantes, calcioantagonistas, IECAS, ARA-II, reductores de lípidos y diuréticos). Como variables de utilización de servicios se incorporaron las pruebas complementarias solicitadas en AP (número de analíticas, radiografías y electrocardiograma), así como el número de derivaciones solicitadas desde AP a cardiología y el número de ingresos en el hospital por IC. A partir del OMI-AP se obtuvo también la fecha de fallecimiento.

Para la selección de las variables de los modelos se realizó primero un análisis bivariado. Por tanto, se trató la variable hospitalizaciones como dicotómica para poder comparar entre los grupos de hospitalizados y no hospitalizados. Las variables cuantitativas se expresaron en medias aritméticas (± desviación típica) y las variables cualitativas en frecuencias absolutas (y porcentajes). En los modelos se introdujeron las variables que resultaron estadísticamente significativas o las que se consideraron más relevantes para los objetivos del estudio en base a la guía de práctica clínica de la Sociedad Europea de Cardiología¹³ (ESC) para el diagnóstico y tratamiento de la insuficiencia cardiaca aguda y crónica.

Para las variables continuas se utilizó la prueba de t de Student o la no paramétrica U de Mann-Whitney cuando no cumplían los criterios de normalidad y homocedasticidad. Para las variables cualitativas se aplicó la χ² y, en caso de que no fuera aplicable, la prueba exacta de Fisher. Para el contraste de hipótesis se fijó un nivel de significación de 0,05 como límite de significación estadística. En los modelos se incluyeron las variables que resultaron estadísticamente significativas en el análisis bivariado y, asimismo, se decidió introducir las variables edad, sexo, la vacuna de la gripe y la hipertensión arterial, al considerarse relevantes para los objetivos de la investigación.

Se ajustaron diferentes modelos de regresión múltiple (Poisson, BN, ZIP, ZINB, Poisson de Hurdle y BN de Hurdle) para evaluar la influencia de factores predictivos en el número de ingresos hospitalarios, debido a que la presencia de sobredispersión implicó que el modelo se tuvo que evaluar con la prueba de razón de verosimilitud. Se comparó el modelo de regresión Poisson Normal con el de ZIP y el modelo de regresión BN con el de ZINB a través del test de Vuong. Para determinar los factores asociados con los ingresos hospitalarios en casos de IC se calculó la razón de tasas de incidencia (IRR) y su intervalo de confianza al 95%. Además, en los modelos de dos partes (inflados con ceros y de Hurdle) también se determinó la probabilidad de tener una hospitalización mediante el Odds Ratio (OR).

Inicialmente, en la parte logit de dichos modelos de dos partes se estimó la probabilidad de no hospitalización. Sin embargo, para poder realizar las interpretaciones de los resultados con mayor comodidad, se cambiaron los signos de los coeficientes β, de tal forma que el modelo de regresión logística calculó la probabilidad de hospitalización.

La comparación de modelos se realizó a través de los estadísticos -2LL y χ² y los criterios de información AIC y BIC. La prueba de Vuong se aplicó para elegir entre un modelo de ceros inflados y el equivalente sin ellos y una prueba de razón de verosimilitud para seleccionar el modelo de regresión ZIP o el modelo ZINB.

Para el tratamiento estadístico y la representación gráfica de los datos se utilizó el paquete estadístico SPSS, v. 22.0. y Stata, v. 14.0.

RESULTADOS

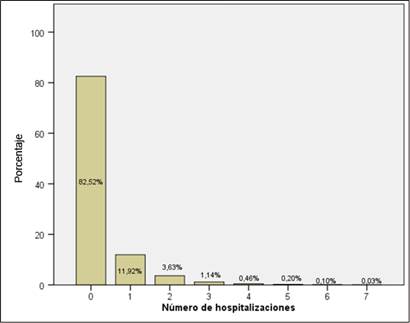
El análisis descriptivo del número de hospitalizaciones registró una media de 0,26 y una varianza de 0,47 siendo esta mayor a la media (sobredispersión). El histograma (figura 1) representó la distribución del número de hospitalizaciones, donde se pudo inducir que el 5,6% de los pacientes ingresaron en múltiples ocasiones.

Figura 1 Distribución de las hospitalizaciones 

En la tabla 1 se recogen las características sociodemográficas, FRCV y comorbilidad asociados, el tratamiento farmacológico y la utilización de servicios según si los pacientes estuvieron o no hospitalizados: la media de edad fue de 76,38 años para los pacientes no hospitalizados y de 76,90 para los hospitalizados. El 96,4% de la cohorte con IC eran pensionistas. De los pacientes hospitalizados el 37,8% eran hombres y el 62,2% mujeres. Además, los pacientes con renta alta fueron hospitalizados en el 19,1% de los casos y hubo un 7,4% más de hospitalizados en la población pensionista que en la población activa (tabla 1).

Tabla 1 Características socio-demográficas, clínicas y de utilización de servicios de los pacientes según si estuvieron o no hospitalizados 

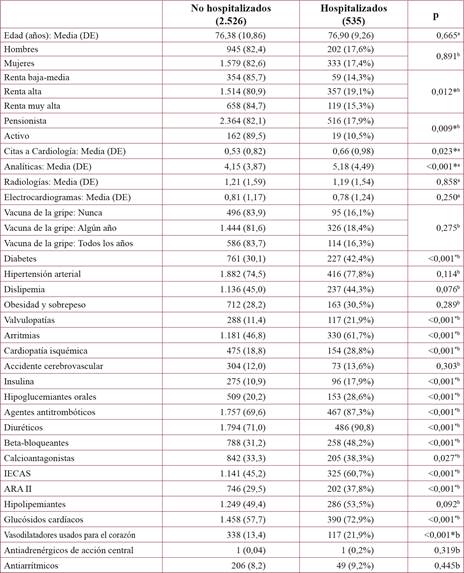
Media y desviación típica (entre paréntesis) de las variables continuas, o valores absolutos y porcentajes (entre paréntesis) de las variables categóricas.^aTest de Mann-Whitney. ^bTest de la chi². ^*Significativo en el nivel 0,05.ARA-II: antagonistas del receptor de la angiotensina II, DE: Desviación estándar, IECA: inhibidores de la enzima de conversión de la angiotensina

Tabla 2 Estadísticos de los modelos de regresión 

Según el análisis bivariado, el nivel de renta, el tipo de usuario, el número de citas a cardiología y de analíticas, la diabete mellitus, las valvulopatías, las arritmias, la cardiopatía isquémica, la insulina, los hipoglucemiantes orales, los agentes antitrombóticos, los beta-bloqueantes, los calcioantagonistas, los IECAs, los ARA-II, los glucósidos cardíacos y los vasodilatadores usados para el corazón estaban asociados a si los pacientes fueron o no hospitalizados (tabla 1). En la cohorte de pacientes hubo 2.526 (82,5%) con cero hospitalizaciones.

El test de Vuong fue estadísticamente significativo tanto para el modelo ZIP (z=9,21; p<0,001) como para el modelo ZINB (z=7,91; p<0,001) confirmando la conveniencia de distinguir dos grupos de pacientes (A y B) debido a un exceso de ceros en la distribución del número de hospitalizaciones.

La hipótesis de sobredispersión se comprobó a través de una prueba de razón de verosimilitud, la cual indicó que es preferible aplicar los modelos BN o ZINB (χ²=227,77; p<0,001), ya que rechazó la hipótesis nula de α=0.

En el modelo ZINB, los pacientes que presentaron valvulopatías (OR=2,01; IC95%: 1,22-3,30) o estaban en tratamiento con antitrombóticos (OR=3,45; IC95%:1,61-7,42) o con diuréticos (OR=2,28; IC95%:1,13-4,58) tuvieron una mayor probabilidad de tener una hospitalización (tabla 3).

Tabla 3 Modelos multivariables obtenidos con los diversos modelos analizados n=3.061 pacientes 

^* P-valor significativo al 5%, ^**P-valor significativo al 1%. ARA-II: antagonistas del receptor de la angiotensina II, BN: Binomial Negativa, IECA: inhibidores de la enzima de conversión de la angiotensina, IRR: razón de tasas de incidencia, OR: odds ratio, ZI: inflada con ceros.

Los factores asociados a una tasa mayor de ingresos hospitalarios fueron tener diagnóstico de valvulopatías (IRR=1,37; 1,03-1,81) o DM (IRR=1,38; IC95%:1,07-1,78) y estar en tratamiento con calcioantagonistas (IRR=1,35; IC95%:1,05-1,73) o IECAs (IRR=1,43; IC95%:1,06-1,92). Haber tenido derivaciones a cardiología tuvo un efecto protector (IRR=0,86; IC95%:0,76-0,97) (tabla 3).

DISCUSIÓN

Los principales resultados del trabajo se dividen en dos partes. Un primer ajuste de los diferentes modelos empleados (encontrar el mejor) y, a continuación, una búsqueda de factores asociados con los ingresos hospitalarios.

La regresión de Poisson es el método más común para analizar datos de conteo. Sin embargo, el no cumplimiento de los supuestos básicos para su aplicación produce estimaciones sesgadas e ineficientes. En nuestros datos se evidencia la presencia de sobredispersión, ya que el valor de la varianza es superior a la media y existen más valores cero de los que cabría esperar a partir de la distribución de Poisson estimada. Por tanto, se han aplicado metodologías alternativas más flexibles, como la regresión BN, los modelos de regresión inflados por ceros o los de regresión de Hurdle. Estos modelos de regresión presentan algunas limitaciones, como que la variable de conteo debe tomar valores discretos no negativos y, en ocasiones, existen problemas de convergencia debido a que la estimación del modelo se realiza con medios numéricos que pueden calcular el estimador de máxima verosimilitud, aunque se han desarrollado estrategias para resolver estos problemas de convergencia¹⁴. También se puede recurrir a modelos de respuesta binaria o multinomial, ya que la sobredispersión se da con menor frecuencia y menor intensidad que en modelos con variable de conteo.

Los resultados aquí identificados muestran diferencias en los estimadores puntuales y los niveles de significación de los modelos analizados. Se rechazó el modelo de Poisson a favor del modelo BN debido a que los errores estándar estaban subestimados por la existencia de sobredispersión. Además, dado el exceso de ceros en la variable de conteo, se compararon los modelos tradicionales frente a los modelos inflados por ceros a través del test de Vuong, rechazándose el BN en favor del ZINB y Poisson en favor del ZIP. También se realizó una comparación del modelo ZIP frente al modelo ZINB a través de una prueba Z, la cual nos indica la necesidad de incluir el parámetro de dispersión α y seleccionar el modelo ZINB. Todos los modelos que han incluido el parámetro de dispersión tienen valores de AIC, BIC y -2LL menores al de Poisson, confirmando así que el supuesto de equidispersión casi nunca se cumple¹⁵. Finalmente, según estos resultados, el modelo con mejor ajuste para el análisis de la variable de conteo ‘número de hospitalizaciones’ es la ZINB, de acuerdo con sus supuestos y los valores de los estadísticos -2LL y χ² y los criterios de información de AIC y BIC.

En investigación clínica y de servicios de salud es común que la variable de interés sea el recuento de eventos de ocurrencia. Diversos estudios identifican el modelo ZINB como el método que ofrece un mejor ajuste para el análisis de datos con exceso de ceros, como son las variables relacionadas con la utilización de servicios de salud^16,17. En este sentido, sería conveniente que los trabajos que aplican modelos de Poisson informen si realmente se cumplen los dos criterios necesarios para su aplicación.

Elegir el modelo de ajuste más preciso tiene consecuencias en la selección de los factores que serán considerados como de riesgo para el ingreso hospitalario. Como se aprecia en los modelos multivariables presentados, los distintos ajustes pueden obtener diferentes factores asociados. El modelo ZIBN no encuentra como significativo los factores Vacunado de la gripe todos los años y Tratamiento con glucósidos cardíacos, pero otros modelos (Poisson, BN, Poisson de Hurdle y BN de Hurdle) lo determinan como factor protector. Análogamente, en este modelo tampoco son significativos factores de riesgo como Tener solicitadas analíticas, Arritmias, Cardiopatía isquémica y Tratamiento con beta-bloqueantes.

La utilización como fuente de información de bases de datos clínico-administrativas puede suponer ciertas limitaciones en relación a la información disponible, tanto en términos de calidad de la misma como de los datos registrados. Una limitación importante es que se considera como caso de IC el diagnóstico por el médico de AP, con la dificultad que ello conlleva al no existir una estandarización del diagnóstico de IC y al no haberse comprobado la existencia de confirmación ecocardiográfica de la sospecha clínica¹⁸. Tampoco es posible establecer si efectivamente se trata del primer episodio de IC. Se han podido perder los casos en los que el sujeto fallezca en un primer episodio de IC aguda sin que se registre el caso diagnóstico en la historia clínica de AP. Tampoco se dispone de información sobre la causa de la IC, del grado de la enfermedad (siguiendo la clasificación NYHA¹⁹) ni de la asistencia en urgencias de estos pacientes o su fracción de eyección. No obstante, aunque esta última se utiliza para definir la IC en dos formas, preservada y reducida, hay planteamientos que sugieren que considerar de forma dicotómica la IC como dos entidades clínicamente diferenciadas que deben abordarse como enfermedades distintas, con fisiopatología diferente y resultados clínicamente diversos, sería una perspectiva demasiado simple²⁰, puesto que no está claro que existan diferencias sistemáticas entre ambos tipos de IC en términos de tasas de reingresos²¹ ni en el pronóstico²² y su mortalidad²³.

La IC es una importante complicación post-infarto que se asocia con muy mal pronóstico y aumenta la mortalidad de los pacientes que lo presentan²⁴. En este trabajo se disponía de información sobre antecedentes de cardiopatía isquémica pero no de altas por infarto agudo de miocardio. La cardiopatía isquémica no se ha visto asociada con una mayor probabilidad de ingresos.

En este estudio se analizaron datos de hospitalizaciones en un solo hospital y cuyo diagnóstico de alta fuese IC. Los pacientes de IC pueden ser dados de alta con diferentes diagnósticos²⁵. Solo se han analizado las derivaciones a cardiología, aunque también podrían haberse derivado a medicina interna, y pueden existir diferencias en la adhesión a los protocolos de tratamiento y uso de recursos entre cardiólogos y otros especialistas²⁶.

Estas bases de datos ofrecen también ventajas, especialmente relacionadas con la perspectiva poblacional y el seguimiento prolongado en el tiempo de un elevado número de pacientes cuya heterogeneidad permite recoger la gran diversidad clínica de un síndrome con la complejidad de la IC²⁷. Por ello, parece clave optimizar la calidad de este tipo de datos para mejorar el conocimiento sobre los resultados del manejo de los pacientes con IC²⁸.

Una de las limitaciones de los datos observacionales tiene que ver con la posibilidad de que se produzca el denominado sesgo de confusión por gravedad. Este se produce cuando la gravedad de la enfermedad se relaciona simultáneamente y de forma independiente con la exposición al tratamiento, en este caso tratamientos con calcioantagonistas, IECAs y con la variable dependiente del estudio, la hospitalización. Este hecho podría guardar relación con la tendencia a utilizar este grupo de fármacos en pacientes con IC más avanzada²². Una explicación alternativa podría ser el sesgo de confusión por indicación, en caso de haber comorbilidad que hubiera motivado dichos tratamientos y que al mismo tiempo hubieran provocado más hospitalizaciones²⁹.

Los antitrombóticos pueden actuar como proxies de la fibrilación auricular, asociada a más reingresos y mortalidad. Los diuréticos identifican a pacientes congestivos, más sintomáticos. Los calcioantagonistas tienen efecto inotrópico negativo y pueden causar empeoramiento de la IC, especialmente en pacientes con disfunción sistólica³⁰.

La relevancia de la comorbilidad para el manejo de la IC es cada vez más importante⁷. Las valvulopatías requieren una importante carga asistencial³¹ y tienen un importante impacto en la supervivencia de la IC³². La diabetes mellitus se asocia con peor estado funcional y pronóstico, ya que es un factor de riesgo independiente de mortalidad, desarrollo de IC e ingreso hospitalario, siendo además frecuente en la IC un mal control de la glucemia²⁸.

Un aspecto también de gran relevancia para entender el impacto de la comorbilidad es el efecto en la capacidad funcional. Dicha información no está disponible para su análisis en este trabajo como tampoco otros factores que también podrían ser importantes en el seguimiento de los pacientes con IC, como parámetros bioquímicos, adherencia al tratamiento o la situación social²¹.

Estudios de base poblacional realizados en otros entornos han identificado otros factores asociados con el incremento del riesgo de hospitalización en la IC. Además de las diferencias en la metodología utilizada habría que tener en cuenta la heterogeneidad de la IC, que se refleja incluso en las diferencias en las características de los pacientes participantes en los ensayos clínicos según dónde hayan sido seleccionados³³. El análisis de los datos que ofrecen fuentes de información electrónicas ya consolidadas en el SNS representa no sólo una oportunidad para la investigación sino una obligación para mejorar la efectividad y calidad asistencial. La diversidad de la IC y las diferencias en la distribución poblacional de los perfiles de pacientes implica la necesidad de localizar la caracterización del riesgo o determinar la efectividad de los tratamientos para individualizar los pacientes con IC en función de sus características específicas y ofrecerles un proceso asistencial adaptado a dichas condiciones. Por tanto, para la búsqueda de factores de riesgo, en muestras con las características presentadas en este trabajo, deben utilizarse distintos modelos, medir su precisión y comparar los factores de riesgo encontrados.