INTRODUCCIÓN

En la publicación anterior se revisaron algunos aspectos de la metodología del metaanálisis, tales como el estudio de la heterogeneidad de los estudios primarios y la detección del sesgo de publicación, característico de este tipo de diseño¹.

En este artículo se continuarán explicando los métodos matemáticos más habituales que se emplean para combinar los resultados de los estudios primarios y se darán unas indicaciones de cómo leer correctamente un diagrama de efectos (forest plot), la herramienta habitual empleada para la presentación de los resultados de un metaanálisis. Finalmente, se propondrá una lista de los aspectos que deben revisarse cuando se valora la calidad de una revisión sistemática con metaanálisis.

MODELOS PARA COMBINAR LOS ESTUDIOS PRIMARIOS

Como ya se comentó en la publicación previa¹, antes de combinar los resultados de los estudios primarios de una revisión sistemática debe comprobarse que estos estudios son homogéneos entre sí, ya que, en caso contrario, tendría poco sentido hacerlo y los resultados que se obtendrían no serían válidos ni podrían generalizarse. Para esto, como ya se describió, existe toda una serie de métodos numéricos y gráficos²,³.

Si se decide que pueden combinarse los resultados de los estudios primarios, esto no puede hacerse uniendo sin más todos los resultados y calculando la media de sus variables de efecto para obtener un resultado resumen global, ya que se correría el riesgo de que se produjese la paradoja de Simpson, según la cual una tendencia que aparece en varios grupos de datos puede desaparecer, e incluso invertirse, cuando los datos se combinan de forma simple⁴.

Esto no debe confundirse con un diseño particular del metaanálisis, el denominado metaanálisis de pacientes individuales⁵, en el que el analista tiene acceso a los datos individuales de todos los estudios, lo que le permite depurar los datos, hacer múltiples análisis estadísticos en todos los estudios, valorar el efecto de las covariables a nivel individual o poder consultar a los autores de los estudios para aclarar las dudas que le puedan surgir sobre metodología o resultados. Todo esto le permite reanalizar cada estudio por separado con una metodología similar y combinarlos con los métodos habituales que veremos más adelante o analizar todos los datos de forma independiente.

Una vez hecha esta aclaración, cuando se elabora un metaanálisis convencional de ensayos clínicos, lo primero que habrá que hacer es valorar los estudios individuales para analizar los estimadores del tamaño de efecto de los estudios y ponderarlos según la contribución que cada estudio va a tener sobre el resultado global.

La forma más habitual es ponderar la estimación del tamaño del efecto por el inverso de la varianza de los resultados, realizando posteriormente el análisis para obtener el efecto medio. Para esto hay varias posibilidades, aunque los dos métodos que se utilizan habitualmente son el modelo de efecto fijo y el modelo de efectos aleatorios. Ambos modelos difieren en la concepción que hacen de la población de partida de la que proceden los estudios primarios.

El modelo de efecto fijo⁶ considera que no existe heterogeneidad y que todos los estudios estiman el mismo tamaño de efecto de la población, por lo que se asume que la variabilidad que se observa entre los estudios individuales se debe únicamente al error que se produce al realizar el muestreo aleatorio en cada estudio. Este error se cuantifica estimando la varianza intraestudios, asumiendo que las diferencias en los tamaños de efecto estimados se deben solo a que se han utilizado muestras de sujetos diferentes. Así, la ponderación de los estudios se realiza por el inverso de su varianza, de forma que el peso de cada estudio es proporcional a su precisión.

Por otro lado, en el modelo de efectos aleatorios⁷ se parte de la base de que el tamaño de efecto sigue una distribución de frecuencias normal dentro de la población, por lo que cada estudio estima un tamaño de efecto diferente. Por lo tanto, además de la varianza intraestudios debida al error del muestreo aleatorio, el modelo incluye también la variabilidad entre estudios, que representaría la desviación de cada estudio respecto del tamaño de efecto medio. Estos dos términos de error son independientes entre sí, contribuyendo ambos a la varianza del estimador de los estudios. El modelo matemático habitual es el método de DerSimonian-Laird⁸, que proporciona un valor τ² que representa esta variabilidad de efectos entre los estudios que no se debe al azar, sino a la diferencia del valor que estima cada estudio con el valor medio global.

Conviene aclarar que, en alguna ocasión, se pueden encontrar metaanálisis en los que los autores utilizan el valor de τ²como medida de heterogeneidad entre los estudios, aunque esto no es del todo correcto. Este parámetro no indica la heterogeneidad en sí, sino la dispersión de los efectos que mide cada estudio en particular.

En resumen, el modelo de efecto fijo incorpora solo un término de error por la variabilidad de cada estudio, mientras que el de efectos aleatorios añade, además, otro término de error debido a la variabilidad entre los estudios. Esta es la causa de que el modelo de efectos aleatorios sea más conservador desde el punto de vista estadístico (más difícil que la medida de resultado resumen sea estadísticamente significativa), ya que la precisión de su estimación es menor, por considerar más factores de variabilidad. Por el contrario, el modelo de efecto fijo es más preciso, pero tiene el inconveniente de que su estimación puede verse muy influida por estudios individuales grandes con estimaciones de mayor precisión (menor varianza).

El tipo de modelo a elegir tiene su importancia. Si el análisis previo de heterogeneidad muestra que los estudios son homogéneos podrá utilizarse el modelo de efecto fijo. Pero si se detecta que existe heterogeneidad, dentro de los límites que permiten combinar los estudios, será preferible utilizar el modelo de efectos aleatorios. En cualquier caso, no debe basarse la decisión sobre cuál modelo utilizar exclusivamente en el cálculo de heterogeneidad estadística, sino que deben considerarse las diferencias clínicas y, ante la duda, utilizar siempre el modelo de efectos aleatorios, aunque sea más conservador⁹.

Otra consideración que hay que tener en cuenta es la de la aplicabilidad o validez externa de los resultados del metaanálisis. Si se ha utilizado el modelo de efecto fijo será comprometido generalizar los resultados fuera de las poblaciones con características similares a las de los estudios incluidos. Esto no ocurre con los datos utilizados con el modelo de efectos aleatorios, cuya validez externa es mayor por provenir de poblaciones de diferentes estudios¹⁰.

En cualquier caso, se obtendrá una medida de efecto medio junto con su intervalo de confianza. La amplitud del intervalo informará sobre la precisión de la estimación del efecto medio en la población: cuánto más ancho, menos preciso, y viceversa.

INTERPRETACIÓN DEL FOREST PLOT

Según la declaración PRISMA¹¹, debemos presentar los resultados de cada estudio individual con un dato resumen de cada grupo de intervención analizado junto con los estimadores calculados y sus intervalos de confianza. Estos datos nos servirán para confeccionar la síntesis de todos los estudios del metaanálisis, sus intervalos de confianza, los resultados del estudio de homogeneidad, etc.

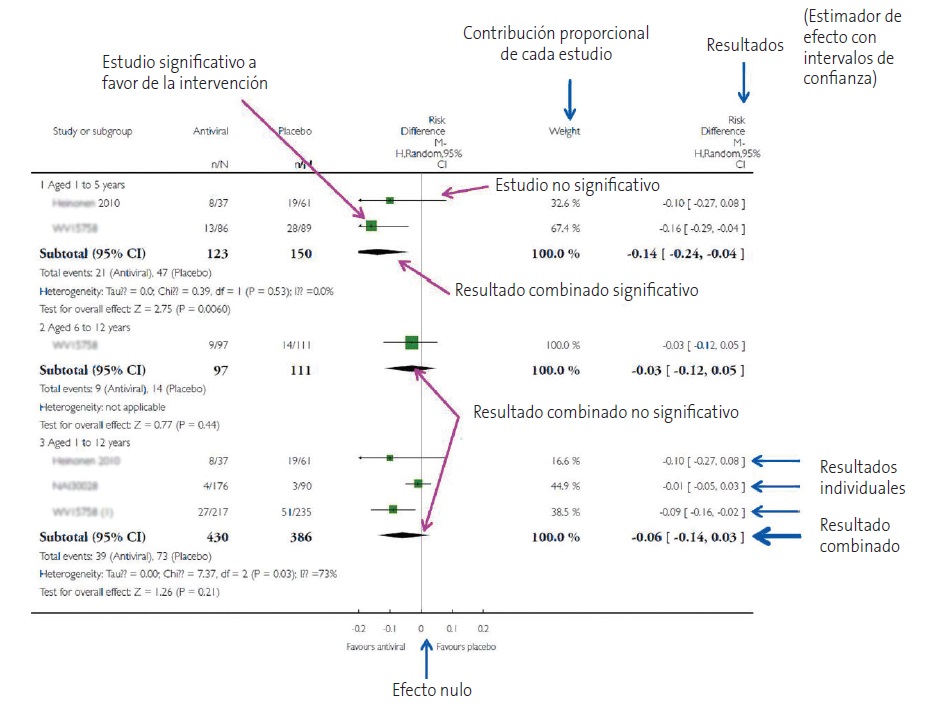
Esto suele hacerse de forma gráfica con el diagrama de efectos o forest plot. Este gráfico es una especie de bosque donde los árboles serían los estudios primarios del metaanálisis y donde se resumen todos los resultados relevantes de la síntesis cuantitativa (Fig. 1). Así, cada estudio se representa por un cuadrado cuya área suele ser proporcional a la contribución de cada uno al resultado global. Además, el cuadrado está dentro de un segmento que representa los extremos de su intervalo de confianza. Si estos intervalos no cruzan el valor nulo de la variable de resultados, este será estadísticamente significativo. La medida resumen se representa por un diamante cuyo centro indica su estimación puntual y su amplitud los márgenes de su intervalo de confianza.

Figura 1. Esquema de la representación de los estudios primarios del metaanálisis mediante un diagrama de efectos o forest plot 

La Cochrane Collaboration recomienda estructurar el forest plot en cinco columnas bien diferenciadas¹² (Fig. 2). En la columna 1 se listan los estudios primarios o los grupos o subgrupos de pacientes incluidos en el metaanálisis. Habitualmente se representan por un identificador compuesto por el nombre del primer autor y la fecha de publicación.

Figura 2. Ejemplo de forest plot 

La columna 2 nos muestra los resultados de las medidas de efecto de cada estudio tal como las refieren sus respectivos autores.

La columna 3 es el forest plot propiamente dicho, la parte gráfica de la representación. En él se representan las medidas de efecto de cada estudio a ambos lados de la línea de efecto nulo, que es el cero para diferencias de medias o proporciones y el uno para odds ratio, riesgos relativos, hazard ratio, etc.

Como se comentó previamente, estos intervalos de confianza informan sobre la precisión de los estudios e indican cuáles son estadísticamente significativos: aquellos cuyo intervalo no cruza la línea de efecto nulo. De todas formas, no hay que olvidar que, aunque crucen la línea de efecto nulo y no sean estadísticamente significativos, los límites del intervalo pueden dar mucha información sobre la importancia clínica de los resultados de cada estudio. Por último, en la parte inferior del gráfico se encuentra el diamante que representa el resultado global del metaanálisis. Su posición respecto a la línea de efecto nulo nos informará sobre la significación estadística del resultado global, mientras que su anchura nos dará una idea de su precisión (su intervalo de confianza). Además, en la parte superior de esta columna encontraremos el tipo de medida de efecto, el modelo de análisis de datos que se ha utilizados (efecto fijo o efectos aleatorios) y el valor de significación de los intervalos de confianza (habitualmente el 95%).

Suele completar este gráfico una cuarta columna con la estimación del peso de cada estudio en tantos por cien y una quinta columna con las estimaciones del efecto ponderado de cada uno. Además, se representa la medida de heterogeneidad que se ha utilizado, junto con su significación estadística en los casos en que sea pertinente.

EN RESUMEN: ASPECTOS PARA VALORAR SOBRE LA VALIDEZ DE UN METAANÁLISIS

Para la correcta interpretación de un metaanálisis, es conveniente seguir una serie de pasos estructurados para no olvidar ninguno de los aspectos clave de su diseño. Una posibilidad es utilizar una lista de verificación, como la ya comentada PRISMA¹¹. Otra, seguir las recomendaciones de la Cochrane Collaboration, que aconseja seguir los siguientes pasos para interpretar correctamente los resultados¹²: