INTRODUCCIÓN
Las fracturas de la extremidad proximal del fémur son un problema muy común en la sociedad actual y de gran importancia ya que, en los últimos años, se ha visto cómo su incidencia ha aumentado en la población. Este aumento se explica en base al crecimiento en la esperanza de vida que se ha experimentado en los últimos años incrementando así la población de la tercera edad y, por ende, las patologías propias de ésta. Es por ello que este es un problema de gran importancia en un país como España en el que en los últimos años se ha experimentado un severo envejecimiento de la población1.
En España son varios los estudios epidemiológicos que describen la incidencia de la fractura de cadera. En la mayoría de los casos se trata de estudios locales y llevados a cabo en cortos periodos de tiempo. También hay estudios de ámbito nacional, aunque en menor medida2. En el documento “La atención a la fractura de cadera en los hospitales del Sistema Nacional de Salud” elaborado por el Ministerio de Sanidad y Política Social en el año 20103 se contabilizan entre los años 1997 y 2008 un total de 487.973 casos de fractura. Se observa además, tanto en estas cifras como en las realizadas en diversos estudios locales2, una predominancia de casos en el sexo femenino y un aumento de la incidencia en la edad con el paso de los años.
Además del gran número de casos conviene reseñar la alta tasa de mortalidad intrahospitalaria (4,71-5,85%) y al año después de la intervención (25-33%)4, y el hecho de que uno de cada cinco pacientes necesitará atención socio-sanitaria permanente2. Es por ello que las fracturas de fémur proximal plantean un reto que ha de ser estudiado en profundidad.
Una vez se ha producido la fractura, el tratamiento, en la mayoría de los casos de fracturas extracapsulares, consiste en la fijación interna de los fragmentos mediante el uso de diferentes dispositivos de osteosíntesis, entre los que se encuentran los clavos intramedulares.
El uso de estas fijaciones mecánicas implica una serie de complicaciones que pueden aparecer después de la intervención. Existen dos fenómenos principales que pueden llevar al fallo de los dispositivos de fijación5: el fallo mecánico del propio dispositivo de fijación y el denominado cut-out. Este último se define como el colapso del cuello femoral dando lugar a un desplazamiento oblicuo y/o rotación de la cabeza femoral ocasionando consigo el daño en el hueso trabecular, y facilitando los desplazamientos del tornillo cefálico6. Un ejemplo de fallo por cut-out se muestra en la figura 1.
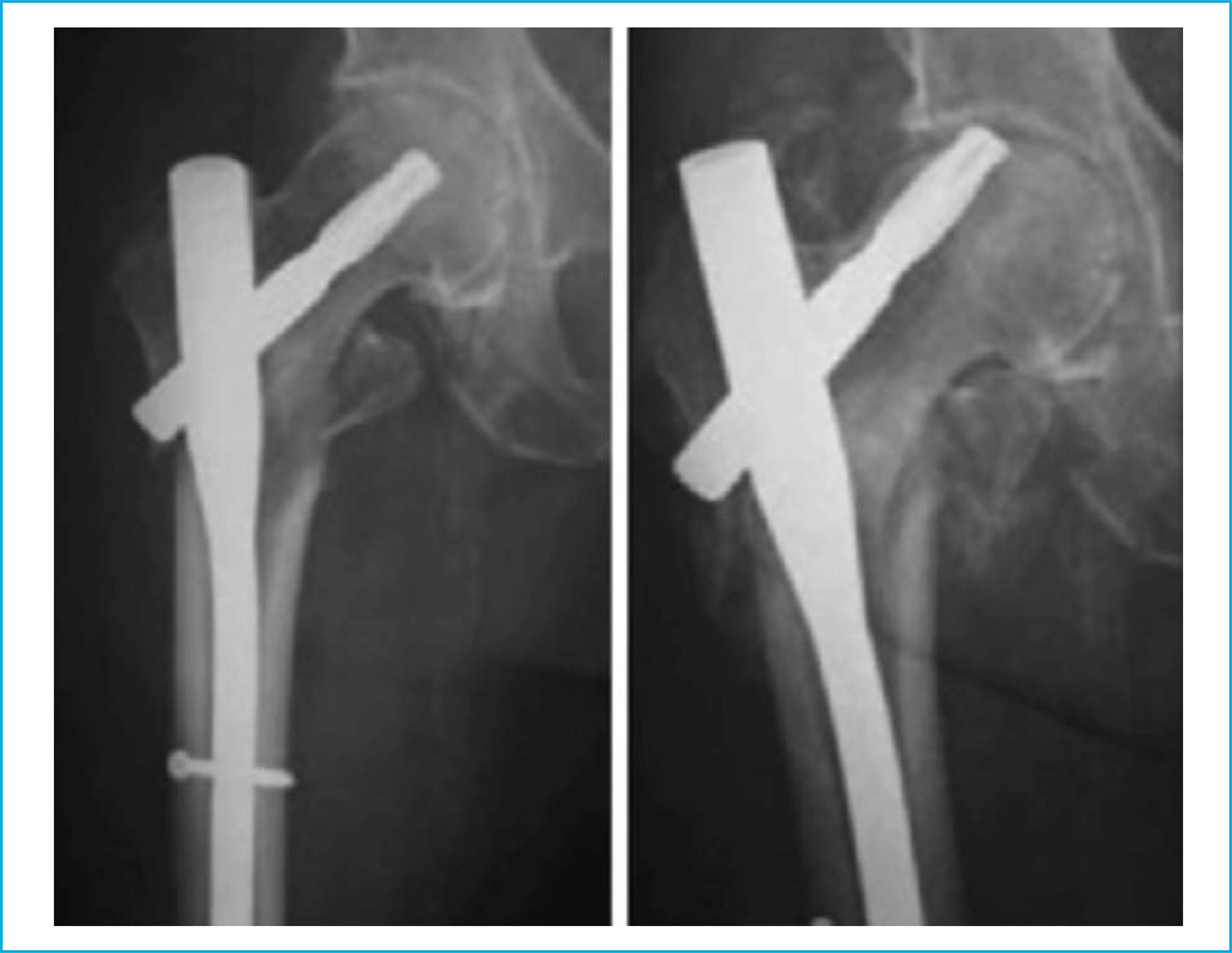
Figura 1. Clavo intramedular implantado como tratamiento a una fractura 31A3 según la clasificación AO/OTA. Espécimen sano (izqda.), fallo del dispositivo de fijación por cut-out (dcha.)7
La incidencia observada es muy superior en el caso del cut-out. Caruso et al. en su estudio8 notificaron una incidencia del 5,6% de cut-out. Wadhwani et al. también concluyen que este fenómeno es el más habitual entre las complicaciones mayores en estas intervenciones9.
Existen numerosos trabajos referentes al fenómeno del cut-out. Los más relevantes para este trabajo son los que analizan su incidencia9 o la importancia de la posición del clavo, ya sea de manera clínica10 o mediante modelos numéricos de elementos finitos11. Otros autores, como Lenich et al., han desarrollado sistemas mecánicos para evaluar el comportamiento mecánico de la estructura fémur-clavo y así analizar los mecanismos de fallo que ocurren en la misma bajo ensayos de fatiga12.
En este trabajo el estudio del cut-out se abordó mediante el método de los elementos finitos. Con este método es posible analizar los esfuerzos y desplazamientos que sufre un fémur debido a una carga externa y bajo unas condiciones realistas13, ya sea en fémures artificiales14 o humanos15. En este caso se simuló un fémur artificial, en el cual se generó de manera numérica una fractura intertrocantérica 31A1 según la clasificación AO/OTA16 que se trataría mediante un clavo intramedular. El motivo por el cual se optó por el estudio en un fémur artificial radica en el hecho de que este ya ha sido caracterizado con anterioridad por varios autores siendo su comportamiento muy similar al fémur humano real17-19. Además, el modelo numérico resulta más sencillo de analizar, ya que tan solo está formado por dos materiales claramente diferenciados, evitando así efectos geométricos referentes a fémures humanos reales.
A partir de estos ensayos, en los que se simularon diferentes posiciones del clavo intramedular, se estudió la variación de una serie de parámetros, tales como rigideces globales del fémur, tensiones y par torsor, y se relacionaron los mismos con el riesgo de fallo por cut-out.
MATERIAL Y MÉTODO
Para la modelización numérica se empleó un fémur artificial (Modelo N.º 3406, Sawbones, Pacific Research Laboratories Inc., Vashon, EE.UU.), que está formado por dos materiales claramente diferenciados que simulan el hueso trabecular y el hueso cortical (Figura 2a). En cuanto al clavo intramedular se ha empleado un modelo PFNA –clavo femoral proximal de antirrotación– (Synthes Gmbh, Oberdorf, Suiza) (Figura 2b).
Obtención de la geometría del fémur artificial a partir de escáner
Para la obtención de la geometría de dicho fémur con la suficiente precisión se optó por la generación de ésta a partir de una tomografía axial computarizada (TAC). El escáner se realizó en un modelo Somatom, SIEMENS, con una resolución de 0,44 mm en el plano transversal y un espesor en los cortes de 1 mm. Mediante este escáner es posible generar la geometría del fémur y diferenciar sus dos materiales (hueso cortical y hueso trabecular) debido a su diferencia de densidades. Posteriormente, mediante la segmentación de imagen y teniendo en cuenta las diferentes escalas de grises (Figura 3a) se obtiene la geometría mostrada en la figura 3b, compuesta por el hueso cortical y el trabecular.
Generación del modelo CAD del clavo intramedular
En este caso la generación del modelo se realizó mediante el software Solid Edge 2019. Para ello, sobre un clavo intramedular real del tipo PFNA, se realizaron las mediciones oportunas para obtener la máxima precisión en el modelo geométrico. En la figura 3c se muestra el modelo geométrico del clavo.
Comportamiento de los materiales a utilizar
El modelo está compuesto por un fémur artificial (hueso trabecular y hueso cortical) y una aleación de titanio correspondiente al clavo intramedular.
a) Fémur artificial
El fémur artificial, como ya se ha explicado anteriormente, está compuesto por dos regiones bien diferenciadas, una correspondiente al hueso trabecular y otra al cortical. En el caso del tejido trabecular se trata de una espuma rígida con unas propiedades similares a las de un hueso trabecular, tratándose en este caso de un material isótropo.
Para el hueso cortical se emplea un material más complejo, una mezcla de fibra corta de vidrio y resina epoxi, siendo en este caso un material compuesto con diferentes propiedades en diferentes direcciones, es decir, un material ortótropo. Ya que no se muestra una dirección principal de las fibras y teniendo en cuenta trabajos previos14, se trata al material como isótropo, ya que se asemeja más a la realidad del mismo.
En cuanto al modelo de material adoptado en el fémur artificial se asumió un comportamiento elástico lineal. Es cierto que, en realidad, el hueso humano posee un régimen elástico y un régimen plástico, y algunos autores han tenido esto en cuenta a la hora de realizar modelos numéricos20,21. Sin embargo, en muchos otros casos se ha analizado el fémur como un material elástico lineal hasta el fallo20,22-24. En este caso, ya que se trabajaría con cargas relativamente bajas que no someterían al hueso a un estado crítico, se consideró como válido un modelo elástico lineal. Las propiedades empleadas en este trabajo para el fémur artificial fueron las obtenidas experimentalmente por Marco et al.14 mostradas en la tabla 1.
Mallado
La malla utilizada en los modelos de elementos finitos está formada por elementos tetraédricos cuadráticos (código C3D10 en Abaqus) de aproximadamente 2 mm de lado. El tamaño del elemento en el clavo intramedular es de unos 1,5 mm de lado. Estos tamaños de elemento se han establecido mediante un análisis de sensibilidad de malla, llegando a variaciones mínimas entre tamaños de elemento consecutivos. En la figura 4 se muestra el fémur con el clavo intramedular y la fractura intertrocantérica modelada en la malla de elementos finitos, para reproducir el comportamiento real del espécimen. La fractura fue generada de manera artificial, aunque también existen distintos métodos numéricos para simular la fractura inicial y la propagación de la misma15,27.
Condiciones de carga
En este caso, el escenario considerado fue el de un individuo en posición ortostática (posición de pie y erecta), considerándose así únicamente la acción del peso propio del individuo sobre el fémur. En el fémur existen también las cargas ejercidas por los músculos que se encuentran actuando sobre este, como el glúteo o el psoas. Sin embargo, para el caso del estudio en el que las magnitudes de interés son tensiones y deformaciones, tal y como demuestra Cristofolini et al.22, no fue estrictamente necesario incluir la acción de los músculos. En este modelo se analizó una carga estática para simplificar el análisis, en la que no se produce movimiento del paciente, aunque ésta pudiera inducir cargas críticas en el fémur que resultarían de interés.
El valor numérico de la carga fue del 75% del peso de una persona promedio, lo que equivale a 551 N para un individuo de 75 kg. La aplicación de la misma se realizó con una inclinación de 8º respecto a la vertical y sobre una superficie que simula la región de contacto de la cabeza femoral con el acetábulo de la pelvis (Figura 5a).

Figura 5. Fuerzas y condiciones de contorno en el fémur. a) Región de aplicación de la carga simulando la zona de contacto de la cabeza femoral con el acetábulo de la pelvis. b) Condiciones de contorno, ángulo de inclinación de la carga y fijación de la región inferior del fémur proximal
En cuanto a las condiciones de contorno, la región inferior del fémur proximal se fijó para que no sufriera desplazamientos, tal y como se muestra en la figura 5b. Estas condiciones son similares a las habituales empleadas en los ensayos experimentales en fémur proximal, en las que la zona inferior se embebe en cemento quirúrgico14.
Colocación del clavo intramedular en el fémur artificial. Posiciones de estudio
En este trabajo se analizó la influencia de la posición del clavo intramedular. Para ello se utilizó como referencia una posición central-central del clavo intramedular, y se varió ±5 mm la posición de éste en las direcciones coronal y sagital (Figura 6):
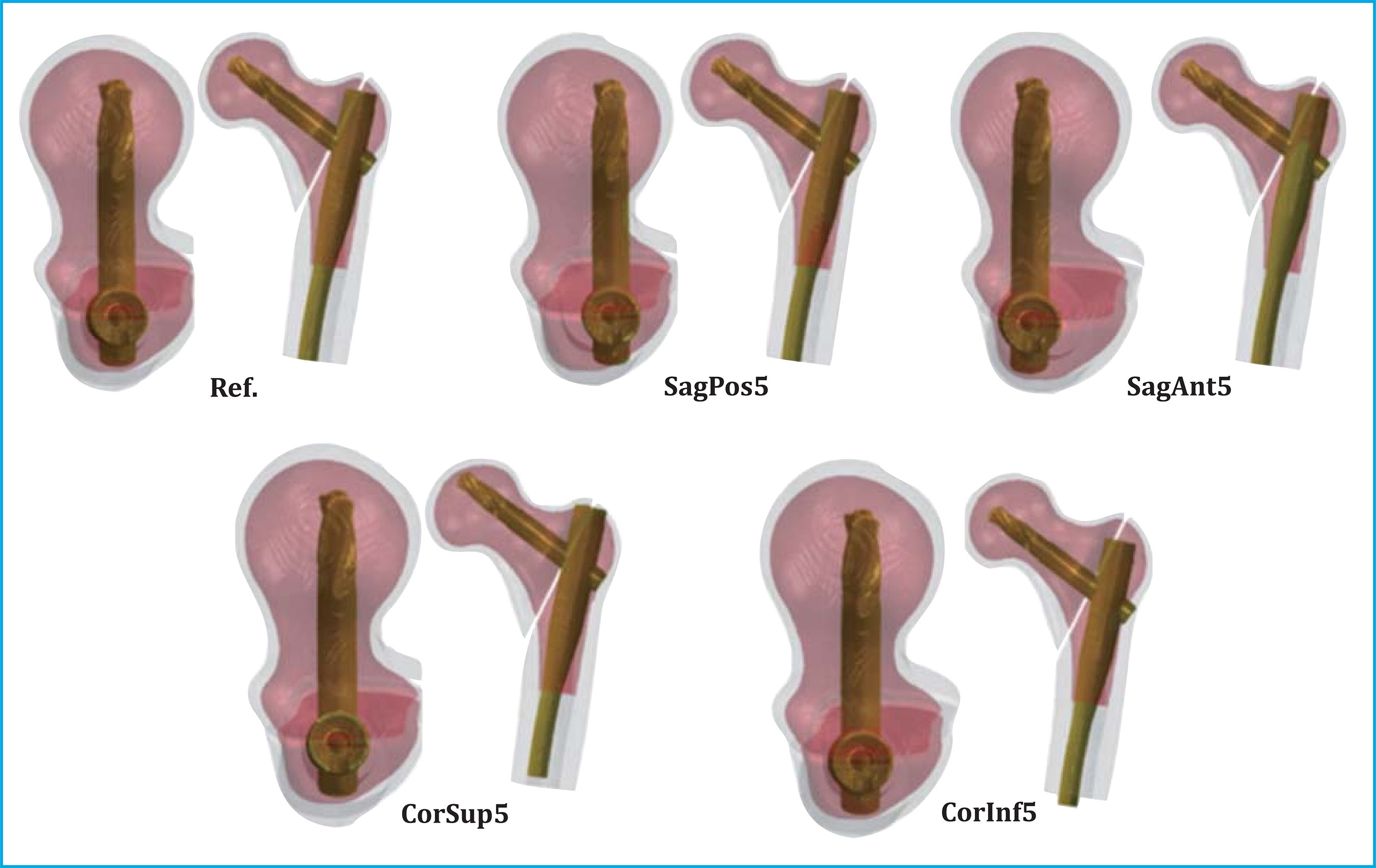
Figura 6. Posiciones de estudio del clavo intramedular. En rosado se muestra el tejido óseo trabecular, en gris el cortical y en dorado el clavo intramedular. Para cada una de las posiciones, a la izquierda se muestra la vista transversal y la derecha se muestra la vista coronal
Posición de referencia: emplazamiento del clavo intramedular tomado como referencia (Ref.).
Desplazamiento de 5 mm en dirección posterior en el plano sagital (SagPos5).
Desplazamiento de 5 mm en dirección anterior en el plano sagital (SagAnt5).
Desplazamiento de 5 mm en dirección superior en el plano coronal (CorSup5).
Desplazamiento de 5 mm en dirección inferior en el plano coronal (CorInf5).
Para evaluar la posibilidad de fallo por cut-out que presentaría cada una de las configuraciones se evaluó un parámetro radiográfico que midiera este riesgo. Este tipo de parámetros suelen basarse en relaciones geométricas relativas a la posición del clavo intramedular con respecto al fémur. En este caso, se optó por el parámetro de Parker28, definido como:
donde ab y ac son las dimensiones que se muestran en la figura 7, tanto en la radiografía anteroposterior (Figura 7a) como en la lateral (Figura 7b).
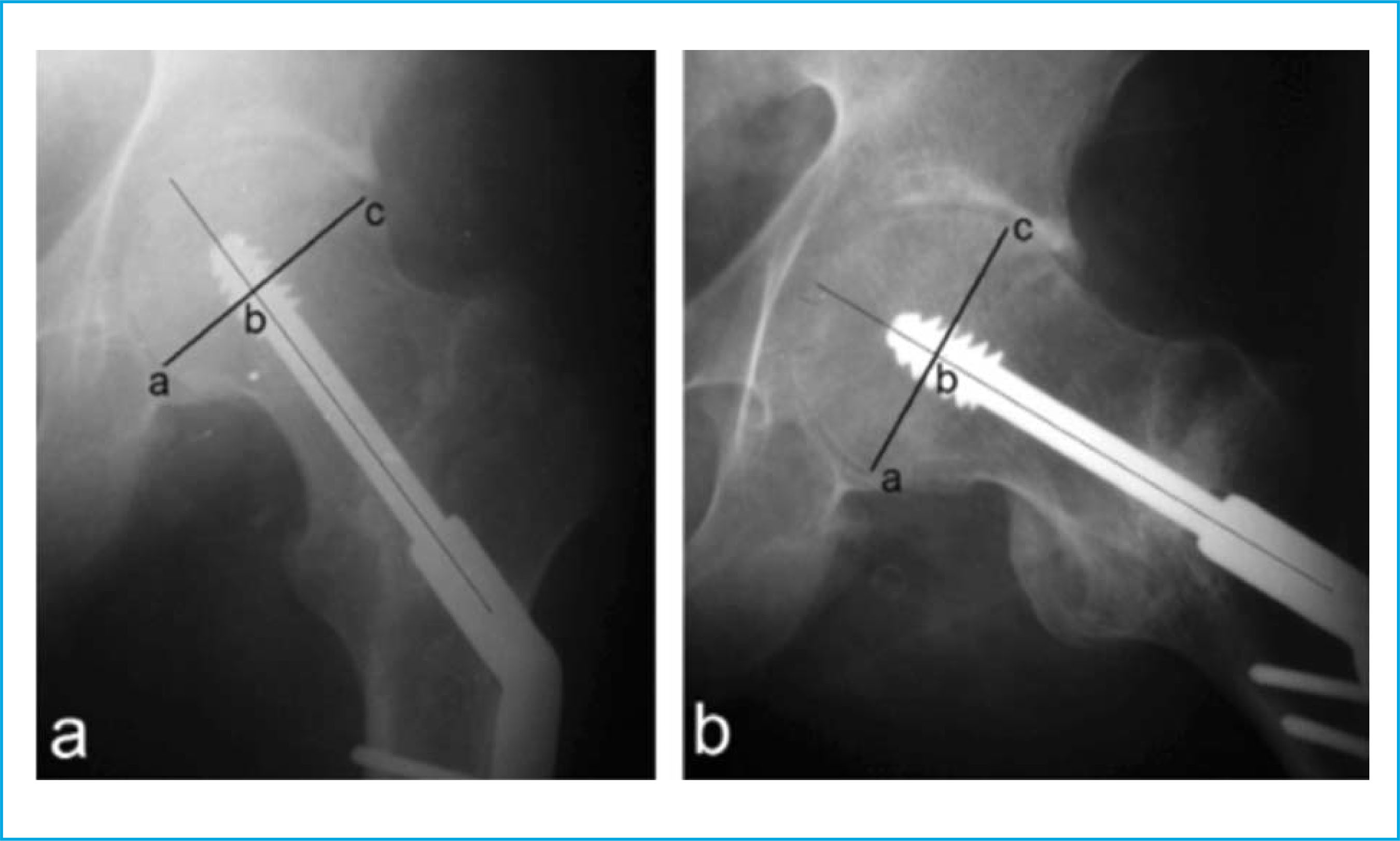
Figura 7. Dimensiones involucradas en el cálculo del parámetro de Parker10. a) Radiografía anteroposterior. b) Radiografía lateral
En la tabla 3 se muestran los valores del parámetro de Parker para las diferentes posiciones estudiadas. Como se puede observar, la posición de referencia mostró un parámetro cercano al 50%, mientras que en el resto de las posiciones los parámetros de Parker se alejaron de este valor.
Parámetros a analizar en el modelo
Gracias al modelo de elementos finitos es posible analizar una gran cantidad de variables que nos pueden ayudar a comprender el fenómeno del cut-out y qué factores contribuyen al mismo. Los resultados objeto de estudio fueron:
Tensión de von Mises máxima en el dispositivo de fijación (σMises). Con este parámetro se establece lo críticas que son las condiciones para la fijación, indicando la posibilidad que hay que se rompa el clavo.
Tensión principal mínima en el hueso trabecular de la cabeza femoral (σmín.ppal). Esta variable determina la compresión que sufre el hueso trabecular debido a la presión ejercida por el clavo intramedular. Cuanto más elevado sea este valor, existen más posibilidades de que se produzcan pequeñas roturas de las trabéculas, dando lugar a holgura entre clavo y hueso y reduciendo la fijación.
Rigidez global del fémur. La rigidez global del fémur puede verse afectada debido a la inclusión del clavo intramedular y la posición de éste. Este parámetro indica el desplazamiento que sufre una estructura debido a una carga determinada, a mayor rigidez menor desplazamiento.
Momento torsor experimentado por el tornillo cefálico (Τt). Nos indica la fuerza de rotación que está sufriendo el tornillo cefálico debido a la unión que existe con el hueso trabecular. Cuanto mayor sea este par torsor es más probable que la fijación no sea capaz de mantener a la cabeza femoral en su posición y se produzca rotación de ésta sobre el clavo.
Modelo numérico de fémur dañado
Finalmente se desarrolló un modelo numérico que simulaba el comportamiento mecánico de un fémur humano con zonas ya dañadas debido a las etapas iniciales del cutout. En este modelo, el hueso trabecular que está en la zona superior al tornillo cefálico se encontraría dañado microestructuralmente, de tal forma que no era capaz de soportar correctamente las cargas a las que se sometiera. Este daño se simuló disminuyendo la rigidez del material de esa zona hasta un 1% del valor inicial. Esto se correspondería con las primeras etapas del fallo por cut-out, en las que el hueso trabecular está ligeramente dañado, de forma que el tornillo cefálico del clavo intramedular no es capaz de fijarse correctamente a la cabeza femoral.
RESULTADOS
En la tabla 4 se muestran los parámetros comentados en la sección anterior para cada uno de los modelos de elementos finitos desarrollados en este trabajo.
Tensión máxima de von Mises
Atendiendo a la tensión máxima de von Mises en el dispositivo de fijación, se obtuvo que dicha tensión siempre se localizó en la región donde se conectan el clavo intramedular y el tornillo cefálico (Figura 8). En dicha zona de coincidencia se obtuvo una concentración de tensiones y, además, la flexión generada por la carga en esta región también fue máxima. También se observó que cuando se descendió la posición del clavo intramedular 5 mm en el plano coronal (CorInf5) se obtuvo un aumento significativo de la tensión respecto de la posición de referencia. En todos los modelos la tensión siempre estuvo muy por debajo del límite elástico del material del clavo intramedular (σy = 900 MPa). De esto último se puede afirmar que el clavo intramedular no sufre esfuerzos críticos cuando se encuentra bajo condiciones normales de carga, y las variaciones en la posición no llegan a provocar el fallo del mismo.
Tensión principal mínima en hueso trabecular
Continuando con la tensión principal mínima en la cabeza femoral, σmín.ppal, en la figura 9 se muestran dichas tensiones en las diferentes posiciones estudiadas. En este caso solo es de interés la zona del hueso trabecular que se encuentra encima del tornillo cefálico. En todos los casos se observó que la mayor compresión (valores negativos implican mayor compresión) tuvo lugar en el extremo del tornillo cefálico, ya que debido a la carga aplicada se produjo una compresión entre la zona de carga y el extremo del tornillo. Esta compresión fue especialmente acusada en la posición CorSup5. La explicación a este hecho radica en que, al posicionar el clavo intramedular 5 mm en dirección superior en el plano coronal, se reduce la masa de tejido óseo trabecular que se encuentra entre el hueso cortical y el tornillo cefálico, incrementándose así la compresión de esta zona de tejido óseo trabecular, que no puede repartir convenientemente la carga recibida. Este hecho también fue corroborado mediante otros modelos de elementos finitos, como el llevado a cabo por Goffin et al.11, en el cual se constató que un posicionamiento en la dirección superior aumenta la compresión en el hueso trabecular y, por consiguiente, el daño del mismo.
Rigidez global del fémur
En cuanto a la rigidez global del fémur, se observó que no fue significativamente afectada al variar la posición del clavo intramedular. Esto implicaba que, en el fémur fijado mediante el clavo intramedular, analizado como una estructura de manera global, la variación en la posición del tornillo no afectaba de manera considerable en la rigidez global de éste.
Par torsor
Finalmente, atendiendo al par torsor experimentado por el tornillo cefálico, se advirtió un especial aumento del mismo en las posiciones SagPos5 y CorInf5. En el caso de la posición SagPos5, atendiendo a la figura 6, se percibió un aumento de la excentricidad del tornillo cefálico con respecto al centro de la cabeza femoral, que contribuyó al aumento del momento torsor. En el caso de la posición CorInf5, el descenso del tornillo provocó una inestabilidad en la fijación, lo que implicó un aumento del par torsor y, por lo tanto, un aumento de la posibilidad de la rotación de la cabeza femoral sobre el tornillo. En el caso de la posición SagAnt5, el par torsor se redujo drásticamente, y esto se debió a la geometría asimétrica que tiene el fémur. Gracias a esta asimetría, esta variación en la posición del tornillo favoreció la estabilidad de éste, aunque en este caso se estaba analizando una carga estática centrada en el plano sagital.
Relación con el parámetro PR
Se tomaron como referencia los valores de 46,47%±9,48 para el caso del PR anteroposterior y de 53,38%±10,00 para el PR lateral obtenidos de Andruszkow et al.29 y se consideró que el riesgo de cut-out se incrementa tanto al aumentar como al disminuir estos valores.
Los parámetros PR estudiados y la relación que guardan con el cut-out se compararon con los valores presentados en las tablas 3 y 4.
Comparando los resultados mostrados en la tabla 3 con los mentados en el párrafo anterior, se advirtió que la posición CorInf5 es la que tiene unos valores más cercanos a estos. Por lo tanto, se tomó posteriormente esta como nueva posición de referencia. Cuanto más difirieran los valores del resto de posiciones respecto a esta, mayor riesgo de cut-out se consideró que entrañarían.
Comenzando por el PR anteroposterior, se advirtió que a medida que este descendía se producía un aumento en la tensión de von Mises experimentada por el clavo intramedular y, por el contrario, cuando aumentaba se producía un incremento en la compresión experimentada por el tejido óseo trabecular. No se observaron tendencias claras entre el PR anteroposterior y el par experimentado por el tornillo cefálico.
Atendiendo al PR lateral únicamente, se obtuvo que el aumento de éste conllevó un aumento del par experimentado por el tornillo cefálico.
Por otro lado, no se observó una relación entre la rigidez global y los parámetros de Parker.
Modelo numérico de fémur dañado
Finalmente se presenta el modelo que simuló el comportamiento mecánico del fémur en las primeras etapas del daño por cut-out. En la figura 10 se muestran los resultados relativos a deformación principal mínima (equivalente a los mayores valores de compresión en términos de deformación) y el campo de desplazamientos de manera global.
En la figura 10a se observa la zona de hueso trabecular que ha sido dañada numéricamente, en la parte superior del tornillo cefálico. Esta zona no fue capaz de soportar la carga correctamente, por ello sufrió grandes deformaciones a compresión, que difierían de las obtenidas a su alrededor. La figura 10b muestra el campo de desplazamientos en el hueso trabecular. En este caso, el modelo dañado sufrió un desplazamiento máximo en la zona de la cabeza femoral 0,02 mm mayor que el fémur sano. Esta diferencia es pequeña, aunque puede ser crítica y llegar a desarrollar mayor daño en las zonas cercanas. En este caso se simuló una zona dañada de hueso trabecular pequeña, de ahí que la variación en los desplazamientos no fuera mayor.
DISCUSIÓN
Atendiendo a las conclusiones extraídas de este trabajo y corroborándolas con el trabajo de Lenich et al.12, resulta bastante evidente que la mejor posición que favorece la biomecánica del fémur con fijación de clavo intramedular es aquella en la que el tornillo se encuentra en la posición centro-centro respecto a los dos planos del cuello femoral. Lenich et al.12 sugiere que mediante este posicionamiento se minimiza el efecto de posibles rotaciones que puedan aparecer entre cabeza femoral y tornillo.
Atendiendo a los rangos de los valores del PR anteroposterior y PR lateral para los cuales existe riesgo de fallo por cut-out, Parker28 establece que el valor de PR anteroposterior para los casos sin incidentes fue de 45%, mientras que para los casos de fallo por cut-out fue de 58%. En los casos de PR lateral fueron de 45% y 36%, respectivamente.
Andruszkow et al.29 realizaron una distinción entre fracturas tratadas con tornillos deslizantes y con clavos intramedulares, además de una distinción del tipo de fractura según la clasificación AO/OTA. En dicho trabajo se obtuvo una media de 46,47%±9,48 para el caso del PR anteroposterior y de 53,38%±10,00 para el PR lateral en las fracturas AO/OTA 31A1 tratadas con un clavo intramedular en las que no ha existido fallo por cut-out, no habiéndose notificado en el mismo ningún caso de fallo por cut-out en este tipo de fracturas tratadas con estos dispositivos de fijación.
Existe una discrepancia sobre si el riesgo de cut-out aumenta o disminuye al aumentar o disminuir este parámetro. Por ejemplo, Parker28 estableció que el riesgo de cut-out aumentaba cuando se tendía a posicionar el dispositivo de fijación más hacia la dirección posterior, lo cual es equivalente a que aumenta el valor de PR lateral. Sin embargo, Baumgaertner et al.6 afirmaron que el riesgo de cut-out aumentaba al posicionar el dispositivo de fijación más hacia la dirección anterior.
Otros trabajos basados en modelos de elementos finitos, como el de Goffin et al.11 se decantan por una posición del tornillo en la zona inferior, para minimizar el daño en el hueso trabecular. Esta conclusión puede ser válida en modelos sencillos en los que la carga es fija, pero en la biomecánica real de la cadera, una posición diferente a la central-central puede dar lugar a elevados pares torsores en determinados momentos de la marcha u otras posiciones, dando lugar a rotaciones de la cabeza femoral que pueden llegar a dañar la zona circundante al tornillo. El modelo numérico de Goffin et al.11 no consideró el par torsor dependiendo de la posición, parámetro que en este trabajo consideramos relevante en el análisis de este fenómeno.
Aunque en este trabajo se analizó un fémur artificial, estos han sido ampliamente estudiados en la literatura, y su comportamiento mecánico es similar al de fémures humanos, tal y como ya corroboraron Cristofolini et al.30 Otra de las debilidades del estudio reside en el uso de modelos numéricos estáticos, en los que no se tienen en cuenta variaciones de la posición de la carga ni efectos dinámicos. En un futuro cercano se espera mejorar el modelo numérico y que éste sea capaz de incluir estos aspectos.
CONCLUSIONES
Las principales conclusiones obtenidas en este trabajo son las siguientes:
Las bajas tensiones de von Mises experimentadas en el dispositivo de fijación con relación a su límite elástico explican la baja incidencia de fallos en estos frente a los fallos por cut-out, por lo tanto, la posición del tornillo no afecta en ningún momento a la integridad del clavo.
Atendiendo al plano sagital, el fallo por cut-out es más probable cuando se desplaza el clavo tanto en la dirección anterior como en la posterior, estando acompañados los movimientos en la dirección posterior con un aumento del momento torsor experimentado por el tornillo cefálico. Esto implica que el clavo no es capaz de fijar la cabeza femoral, dando lugar a una rotación del mismo.
Atendiendo al plano coronal, el fallo por cut-out tenderá a producirse cuando se desplaza el clavo intramedular en la dirección superior, estando este fallo relacionado con una compresión del tejido óseo trabecular. Los desplazamientos en la dirección inferior contribuirían a evitar este fallo, pero conllevaría una mayor carga para el dispositivo de fijación y aumento del par torsor en condiciones biomecánicas realistas.
Teniendo en cuenta la biomecánica real de la cadera y las rotaciones de la misma en actividades de la vida diaria, la posición más segura del componente cefálico en fracturas inestables rotacionalmente es centro-centro.
Mediante los modelos numéricos se ha comprobado que es posible incluso simular las primeras etapas de cut-out, en las que una zona dañada puede dar lugar a pequeños desplazamientos, que posteriormente pueden llegar a aumentar el daño, desencadenando finalmente el fenómeno mencionado.











 texto en
texto en