Sr. Director
Se me ha llamado la atención sobre el artículo redactado por Pérez Castillo et al. (2020)(1) para explorar la probable relación entre la ocurrencia de lesiones musculoesqueléticas y la composición corporal de futbolistas profesionales(1). Según los autores, la composición corporal del deportista, reconstruida de la suma de los pliegues cutáneos, podría determinar el riesgo de ocurrencia de tales lesiones (definidas éstas en el artículo citado como esguinces de la rodilla y/o el tobillo)(1). En 28 futbolistas se contabilizaron 11 lesiones, válido para un 39,3 % del tamaño de la serie de estudio(1). La suma promedio de 6 pliegues cutáneos fue de 62,2 ± 47,9 mm(1). Los investigadores encontraron que la aparición de las lesiones se correlacionó estrechamente con la sumatoria de los pliegues cutáneos(1). No solo eso: se demostró que en los atletas no lesionados la sumatoria de los pliegues fue de 32 – 69 mm; mientras que, en los lesionados, la suma de los pliegues fue mayor de 70 mm(1).
Existe un abundante cuerpo literario que ha provisto modelos matemáticos para la reconstrucción de la composición corporal del deportista profesional(2 3 4 5). Todos estos modelos persiguen estimar el tamaño de la masa muscular esquelética, por cuanto es el factor biológico que determina el éxito deportivo, y es, por lo tanto, el objetivo de los programas de acondicionamiento físico. Siguiendo la línea de pensamiento esbozada, la efectividad de los programas de acondicionamiento físico resultaría en un mayor número de medallas, trofeos, campeonatos y récords individuales y colectivos. Es inmediato que lo anterior se lograría con una tasa mínima de lesiones musculo-esqueléticas para asegurarle así al deportista una larga (y también exitosa) carrera profesional.
Lo contrario también sería cierto. Si a la conclusión del programa de acondicionamiento físico se observan pocos cambios en la masa muscular esquelética (o complementariamente: una mayor masa grasa corporal que la aceptada según las exigencias del deporte en cuestión), entonces cabría anticipar un pobre desempeño físico en las competencias previstas, junto con una mayor incidencia de las lesiones tan temidas, y una vida profesional acortada(6).
Tal (loable) propósito tropieza no obstante con varias dificultades metodológicas, desde la definición de un protocolo de captación de las variables antropométricas de interés, la elección del mejor modelo de reconstrucción de la composición corporal (como los autores citados más arriba mencionaron en el trabajo reseñado, pero sin brindar evidencias de ello), y la correcta interpretación de los hallazgos. Y es aquí donde quiero detenerme. Los investigadores apelan a un modelo de regresión lineal simple para modelar la relación probable entre las lesiones ocurridas y la suma de los pliegues.
Las maquinarias de regresión lineal1 2 basadas en los mínimos cuadrados tratan de encontrar aquel juego de parámetros (léase también los coeficientes del sistema | modelo de predicción) que haga mínima el cuadrado de la diferencia entre el valor observado de una variable dependiente y el esperado(7). La regresión lineal simple sería una de las posibles modalidades de la regresión de mínimos cuadrados, y ofrecen una primera aproximación al problema a resolver al solo considerar 2 parámetros: un intercepto y una pendiente. Pero debo advertir que siempre será posible encontrar otro modelo con 3 (y más también) parámetros que ofrezca una suma de los cuadrados de los residuales menor3.
Existe otro “pero” en el caso del uso de un modelo de regresión lineal de mínimos cuadrados como solución del problema de la modelación de la ocurrencia de lesiones según la suma de los pliegues cutáneos. Para que los parámetros no sean sesgados (y que el error de estimación de los mismos se mantenga “controlado”), la variable independiente (también denominada en estas lides como predictora) debe medirse sin error4. Por su parte, la variable dependiente muchas veces se hace corresponder con realizaciones dispuestas en una escala numérica real. Ello no es el caso aquí. Las lesiones musculoesqueléticas son realizaciones binarias. Esto es: por propia definición la lesión solo puede existir en dos estados excluyentes y a la vez complementarios: Ausente vs. Presente. Trasladado a una escala binaria: Ausente ≡ 0 vs. Presente ≡ 1.
Por estas razones, tratar de describir la relación entre la ocurrencia de las lesiones musculoesqueléticas y la suma de los pliegues mediante un modelo lineal de regresión de mínimos cuadrados es contraproducente, y solo coloca a los investigadores en una situación en la que tienen un resultado (como el que se refleja en la Gráfica 2) que no ofrece claridad sobre la relación que se desea encontrar.
¿Qué hacer?
Primero, hay que trascender el modelo de regresión lineal de mínimos cuadrados, e introducir el concepto de “riesgo”(8). Esto es: en condiciones naturales los atletas salen a competir libres de lesiones. Por el propio hecho de la actividad deportiva, el deportista está siempre en riesgo de lesionarse, si bien el programa de acondicionamiento físico busca minimizar tal riesgo.
Introducido el concepto de riesgo, entonces podemos recurrir a una regresión logística como la mejor maquinaria de regresión para describir la relación que se desea(9). A partir de un conjunto (mejor se diría un vector) de covariables (que en el caso que nos ocupa se limitaría a solo una, pero que pueden ser varias), el juego final de parámetros que se obtenga describe cuán propenso es el deportista a sufrir una lesión si muestra un valor determinado de la suma de los 6 pliegues cutáneos.
La probabilidad de que ocurra una lesión estaría dada por la expresión siguiente:
En la expresión anterior: X’β: producto de la multiplicación de los vectores contentivos de las covariables y los parámetros del modelo.
De la inspección de la expresión presentada previamente se desprende que la regresión logística cae dentro del dominio de los modelos no lineales, y la solución se aparta ostensiblemente de la propuesta por la regresión lineal. Sin embargo, cualquier paquete de análisis estadístico-matemático contempla como opción la regresión logística. Incluso, la regresión logística puede ser programada dentro de una hoja EXCEL©® de cálculo empleando la extensión VisualBasic©® para EXCEL©®.
La Figura 1 muestra los dos modelos empleados en el análisis de la misma relación. Como se aprecia en la imagen que ocupa el panel inferior, la relación entre la ocurrencia de las lesiones y la suma de los pliegues es en realidad sigmoide, con una probabilidad muy escasa de sufrir una lesión para sumas de pliegues < 60 mm, probabilidad que se incrementa rápidamente a partir de este valor hasta hacerse casi universal para sumas de los pliegues > 90 mm. La regresión logística también nos devolvería cuál sería la razón de disparidades (del inglés odds-ratio) implícita en la ocurrencia de la lesión de acuerdo con el valor de la suma de los pliegues como para hacer inferencias pertinentes a un jugador seleccionado. Un atractivo adicional de la regresión logística sería el cálculo de la OR de la lesión si se incluye junto con la suma de los pliegues la posición del futbolista dentro del campo. Así, se podría establecer si las lesiones suelen ser más frecuentes entre los delanteros, por ejemplo, en virtud de la posición de avanzada que desempeñan.
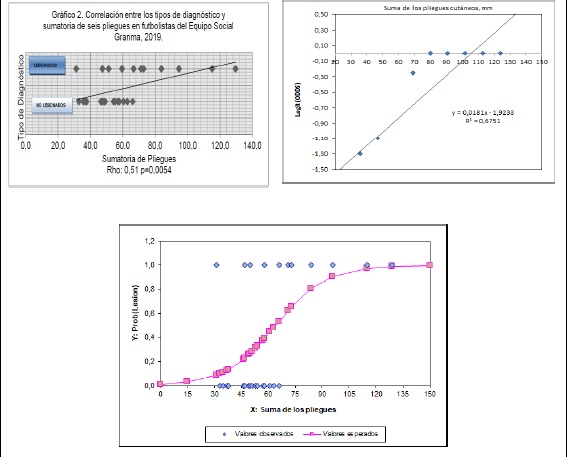
Figura 1. Representaciones gráficas de las asociaciones entre la ocurrencia de lesiones musculoesqueléticas y la suma de los pliegues cutáneos en futbolistas profesionales. Panel superior. Izquierda: Lesión presente (Y = 1) vs. Sumatoria de los pliegues. Derecha: Logit = Log(Odds) vs. Sumatoria de los pliegues. Panel inferior. Probabilidad de ocurrencia de la lesión vs. Suma de los pliegues. Leyenda: ODDS: Posibilidad de ocurrencia de la lesión. La ODDS se estima como la proporción de aquellos futbolistas con lesiones (Y) respecto de los incluidos en un estrato de distribución de la suma de los pliegues cutáneos (N) que están libres de lesiones (Q): ODDS = Y/(N – Y) = Y/Q. En condiciones naturales: ODDS > 0. En ocasiones se añade 0.5 en ambos miembros de la ODDS para mejorar la estimación de los parámetros logísticos: ODDS = (Y + 0.5)/(Q + 0.5).














