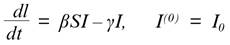INTRODUCCIÓN

Transcurrido casi un año desde que en el mundo se tuvo consciencia de que algo estaba surgiendo en China que suponía una seria amenaza a la salud mundial, como así ha sucedido, la declarada «pandemia de COVID19»¹, es ya una realidad absolutamente planetaria que, como se suele decir últimamente, «ha venido para quedarse».

Un agente viral, por lo demás viejo conocido de la Medicina, como causante de patología más o menos banal, como el resfriado común, ya nos dio el primer susto con el brote de SARS en 2012, que afortunadamente no pasó de un susto. Pero el actual coronavirus, SARS Cov2, es otra cosa, desde todos los puntos de vista que se quiera ver. Por el impacto que está provocando y, fundamentalmente, por el nivel de confusión que está generando a la ciencia médica, más parece procedente de algún meteorito que haya impactado en la Tierra, a juzgar por el grado de desconocimiento que sobre él se tiene y la gran cantidad de sorpresas que nos está deparando.

La realidad a la que nos está sometiendo, para casi todos los aspectos de la ciencia médica está resultando un desafío especialmente amenazador.

El hombre de la calle, a fuerza de las continuas noticias que aparecen en los medios de comunicación, ya ha aprendido a saber qué es la Epidemiología y sus indicadores que nos mantienen en vilo al subir o bajar cada día que pasa. Si a esto se acompaña el «síndrome de sobrecarga de información» provocada por la inmensa cantidad datos e informaciones que se reciben por los medios oficiales y redes sociales, esta pandemia viene asociada por una «infodemia», que muchos dudan si es más peligrosa esta que aquella.

Y dentro de la ilimitada catarata de información que está generando esta pandemia, ya empieza a serle familiar a la gente, los múltiples esfuerzos que se están llevando a cabo en todo el mundo a la búsqueda de modelos de simulación que nos permitan anticiparnos a los movimientos de nuestro enemigo. En este sentido, al consultar la literatura, la cantidad de ensayos que se están haciendo son muchos y muy importantes.

La casi totalidad de los modelos matemáticos que se están desarrollando en el mundo, tienen su base conceptual en el modelo SIR (Susceptibles, Infectados y Recuperados), desarrollado en 1927 por el bioquímico William Kermack y el Coronel médico y epidemiólogo escocés Gray McKendrick². Este último, diseñó la función de regresión logística del crecimiento bacteriano.

Es importante explicar las bases de este modelo, porque de alguna forma, todos los modelos que se han desarrollado desde entonces se basan en sus fundamentos.

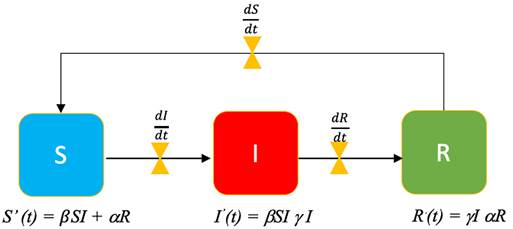
El gráfico refleja por sí mismo, el escenario que se pretende modelizar.

Susceptibles (S), estado en el cual el individuo puede ser contagiado por otra persona que esté infectada;

Infectado (I), estado durante el cual el individuo se halla infectado y puede además infectar a otros;

Recuperado (R), o curado. Estado durante el cual el individuo no puede ni ser infectado por haber adquirido inmunidad (temporal o permanente) ni infectar (por haber recuperado o haber pasado la etapa contagiosa de la enfermedad).

Figura 1 

Un recuperado puede volver a ser susceptible, en el caso de no haber adquirido suficiente carga inmunitaria. Así, entre las enfermedades infectocontagiosas encontramos dos grupos principales:

El modelo de Kermack y McKendrick es tal que puede tener en cuenta la dinámica vital de la población (nacimientos, muertes, movimientos migratorios) dependiendo del horizonte temporal analizado, y de las características de la enfermedad y de la población estudiada.

Si denotamos por N a la población total al tiempo t en la que el brote epidémico puede ocurrir, y por S(t), I(t) y R(t) a los individuos en estados susceptible, infeccioso y recuperado o muerto al tiempo t respectivamente, entonces N = S(t) + I(t) + R(t) es constante. La tasa de infección que determina el número de individuos por unidad de tiempo que se transfieren del compartimiento de susceptibles a infecciosos depende el número de contactos per cápita µ que una persona sana y susceptible tenga por unidad de tiempo, y de la proporción τ de estos contactos que sean con individuos infecciosos que le transmitan la enfermedad. Con este razonamiento, si denotamos por β = mt a la tasa per cápita de transmisión de enfermedad, entonces la tasa de infección esta dada por la expresión βS(t) I(t). La tasa de recuperación o muerte la denotaremos por γ. De hecho, el inverso de esta tasa es el tiempo promedio que un individuo de la población permanece enfermo (e infeccioso) cuando suponemos que la distribución de tiempos de residencia en el comportamiento de infecciosos sigue una distribución exponencial. Podemos ahora escribir la ecuación diferencial que describe el cambio en el número de individuos pertenecientes al comportamiento infeccioso.

donde I ₀ representa el número inicial de personas infecciosas en la población. Un brote epidémico se iniciará cuando el número de gente infecciosa se incremente una vez que los primeros casos son introducidos en la población (que originalmente supondremos conformada solamente por gente sana y susceptible). En términos de la ecuación anterior la condición enunciada significa que buscamos condiciones para que dI / dt > 0.

El Modelo como tal se expresa como:

S’ = ‒βSI, I’ = βSI ‒ γI, R’ = γI

siendo S la población susceptible de enfermar, I la población infectada, y R la población que ha pasado la enfermedad y se halla recuperada. Existen dos constantes que son la tasa de infección b (beta) y la tasa de curación o recuperación g (gamma).

Y así, la ecuación clave del modelo es la que refleja, por unidad de tiempo, el número de casos. Infectados en tiempo t + 1 = infectados en tiempo t + nuevos casos ‒ nuevos curados.

I _(t+1) = I _(t) + βSI ‒ γI,

A partir de esta base matemática, se han desarrollado, como hemos referido anteriormente, prácticamente todos los modelos matemáticos, basados en cálculo analítico. De los más elaborados, es importante referir el desarrollado por el equipo del MOMAT, de la Fad. de Matemáticas de la Universidad Complutense de Madrid³.

Figura 2 

Basado en el modelo SEIR (E: expuestos), es importante la separación que ha hecho de los casos detectados frente a los no detectados, los asintomáticos, elemento θ que sin test de screening, no se puede saber ni quiénes, ni cuántos son y ni si son o no contagiosos.

El equipo de la Universidad de Valencia ha desarrollado otro modelo similar⁴.

Y como estos, se han desarrollado modelos por todo el mundo, siendo también un referente conocido el del «Imperial College of London»⁵, o la John Hopkins.

El presente trabajo se caracteriza por desarrollar el modelo utilizando una herramienta de simulación dinámica, denominada «Dinámica de Sistemas» (DS)^6,7, bastante utilizada en simulación industrial, urbana y en análisis prospectivo de la sociedad. Con esta herramienta, se han construido también modelos, basados todos, de alguna manera en el modelo SIR⁸.

OBJETIVO

El objetivo del presente trabajo es el desarrollo de un modelo matemático de la evolución de la epidemia de COVID19 en la comunidad de Madrid, mediante la técnica denominada «Dinámica de Sistemas (Modelo DS)», con una complejidad suficiente como para, sobre él, poder analizar la «complejidad dinámica» que la epidemia está mostrando, en comparación con los otros muchos modelos desarrollados al respecto. Se entiende como complejidad dinámica al diferente comportamiento de un sistema (social, en este caso) a corto, medio o largo plazo, dado que sus comportamientos no son iguales a corto, medio y largo plazo.

MATERIAL

Para el diseño y desarrollo del Modelo DS sobre la pandemia COVID 19, se ha utilizado el software de Ventana Systems Inc®, Vensim PRO® versión 8.1 (la actual de 2020), sobre un ordenador Mac Mini con sistema operativo MacOs Catalina 10.15.7 con procesador Intel Core i5 de doble núcleo, con datos, para su calibración, de la Comunidad Autónoma de Madrid, tomados de las fuentes oficiales del Instituto de Salud Carlos III y recogidos en la referencia bibliográfica.

El manual de usuario de VensimPro 8.1 se puede encontrar en la web de Vensim:

https://vensim.com/vensim-8-1-release/

MÉTODO

La metodología empleada se basa en el uso de la técnica «Dinámica de Systemas» (Systems Dynamic). Esta es una metodología de modelización de modelos matemáticos, diseñada por Jay Forrester, en el Instituto Tecnológico de Massachusetts (MIT) en la década de 1960-69, inicialmente para el estudio de las fluctuaciones del mercado⁶, aunque después fue extendiéndose a la dinámica urbana⁹ y finalmente mundial^10,11, siendo la metodología empleada en los primeros informes prospectivos a muy largo plazo de la Humanidad en los primeros informes al Club de Roma^12-14 Esta técnica matemática, permite convertir modelos de diseño mental y modelos matemáticos dinámicos con capacidad de reproducir fenómenos reales y efectuar proyecciones a futuro. Se ha empleado en infinidad de disciplinas, aunque especialmente en el sector empresarial y medioambiental. Las herramientas de diseño fundamentales son Stella y Thinker^15,16. No es una metodología al uso en ensayos clínicos, porque tiene como finalidad el diseño de simuladores de cualquier tipo de sistema físico, biológico o social.

El método de diseño final del modelo DS de COVID 19, consta de tres fases. La primera es la elaboración del modelo mental, donde en el texto, se describe las características del sistema que se quiere modelizar, y donde tan importante es el sistema en sí, como sus ligaduras externas con sistemas exteriores a los que afecta y que le afectan. El objetivo es tener un modelo mental «macro», es decir, un «overwiew», un amplio panorama de la realidad que queremos modelizar, aspecto muy importante porque si algo es esencialmente fundamental, es el establecimiento de los «límites del sistema», unos límites necesariamente artificiales, dado que la realidad es toda ella «una», sin divisiones, a las que tenemos que acudir para poder comprender lo que sucede. Es decir, tenemos que poder observar el bosque, para ubicar el sector que queremos estudiar con detalle, pero sin perder la perspectiva del conjunto, porque tanto sucede que el exterior influye en el interior del sistema y viceversa y, de qué modo, como vamos a ver.

Elaborado el primer modelo mental global, que trataremos de representar con un general «modelo causal», acotaremos los límites del sistema, volviendo a iterar de nuevo un nuevo modelo mental con los límites acotados, representado con su correspondiente modelo causal.

Elaborado el segundo modelo mental, haremos la tercera iteración, elaborando el modelo mental y causal del modelo matemático DS.

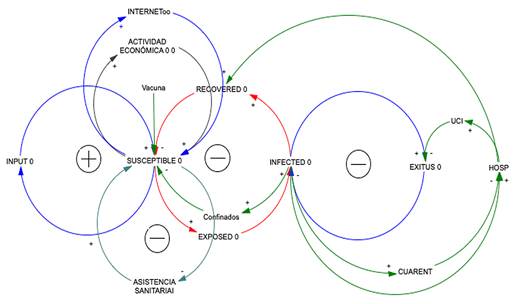
Modelo mental de la primera iteración

1. Una epidemia surge en el contexto de un sistema humano normal, donde una población experimenta una dinámica normal de entradas (nacimientos, inmigración y visitas) y de salidas (fallecimientos, emigración y salidas por desplazamientos).

2. En este contexto, sus habitantes desarrollan un sin fin de actividades humanas de carácter social y económico que reflejan la vida de la comunidad.

3. Por otro lado, la posibilidad cierta de contraer todo tipo de enfermedades infecciosas y no infecciosas, requiere la existencia de un sistema sanitario capaz de prevenir y tratar las diferentes dolencias de sus habitantes.

4. Los flujos de entrada y salida de población, tanto por cambio de residencia (inmigración y emigración), como por desplazamientos por razones personales y de trabajo, generan un intercambio tanto más intensos cuanta mayor relación tienen diferentes zonas entre sí. Algo similar al poder de atracción que los cuerpos experimentan debido a la Ley de la Gravedad. El hecho cierto es que es casi imposible que una zona geográfica se mantenga aislada sin comunicación con el exterior.

   Estos cuatro considerandos expresan el sistema dinámico de una población normal, donde cada uno de estos cuatro elementos se puede expresar de ilimitadas formas e intensidades y se expresa en lo que los informativos nos muestran diariamente en las noticias.

5. En los sistemas sociales actuales, en los últimos veinte años ha emergido con muchísima intensidad el «ciberespacio», espacio virtual vehiculado por Internet, por donde casi algo más que la información se desplaza a la velocidad de la luz de un extremo a otro del Planeta y llega a cientos o miles de millones de personas.

Figura 3 

Modelo mental de la segunda iteración

Entramos ahora en el suceso epidémico, que sucede por la introducción de un sujeto parásito, bien sea un gusano, un hongo, protozoo, bacteria, virus o un prion, en la comunidad.

Todas las especies tienen un conjunto de factores que determinan su crecimiento y su disminución en número. Se reproducen en una proporción tan grande que su número aumentaría considerablemente si solo murieran por accidente o vejez. Y el tiempo de duplicación en número, por esa tasa de crecimiento es mucho mayor que el que le correspondería por dicha tasa. Y los dos factores limitantes de ese crecimiento es 1) la disponibilidad de alimento y 2) la actividad de sus depredadores¹⁷.

Cada especie tiene dos tipos de depredadores, los que son capaces de capturarla y devorarla como alimento (predadores) y los que son capaces de invadirla por dentro (los parásitos). También los hay a medio camino, como los insectos o los vampiros.

La finalidad de ambos (de los tres) es la misma, obtener alimento y capacidad reproductiva, es decir, la supervivencia. Es decir, la actividad central de un ser vivo es obtener alimento y evitar ser devorado.

Figura 4 

Los animales mayores que están en la cúspide de la cadena alimenticia y, no tienen pues competidores ni depredadores, son sin embargo atacados y en su caso muertos por los que están en el escalón microscópico de la cadena, por los microorganismos. El tigre es el rey de la jungla, pero muere por, las lombrices que le acribillan los pulmones.

Es decir, la enfermedad infecciosa es un acontecimiento rigurosamente normal en la biología. Y lo que sucede, cuando esa enfermedad infecciosa es además, transmisible, es decir, contagiosa, es que, en la dinámica poblacional que hemos visto en la primera iteración, se introduce una segunda entre las entradas y las salidas, que convierte a la variable «población», en dos grupos, los «susceptibles» o personas sanas de la enfermedad y en «infectados», personas capaces de transmitirla. Más un tercer grupo que son los «recuperados», personas que han sufrido la enfermedad, no han muerto y vuelven a recuperar la salud pero con sus defensas capaces de rechazar una nueva infección por el mismo agente.

En esta situación, como sabemos, todo se altera, la actividad económica decae de forma brusca y repentina, las relaciones sociales se tensan, surge el miedo, la información fluye de una forma descontrolada y muy distorsionada y, por supuesto, el sistema sanitario se resiente por el incremento de casos y de ingresos en los hospitales.

Es en este escenario básico, donde William Kermack y A. Gray McKendrick, desarrollaron su conocido modelo de epidemias SIR, SEIR, al que me he referido en la introducción.

Modelo mental de la tercera iteración

Si la segunda iteración representa la dinámica de la epidemia de modo inercial, es decir, sin respuesta sanitaria ni social activa, salvo la de atender a los enfermos de su dolencia física, en esta tercera iteración, introducimos la respuesta sanitaria, social y política al problema, con la imposición de medidas preventivas de contención y mitigación, con restricciones a la movilidad, la imposición de elementos protectores, medidas de higiene, que todos ya conocemos. Además se incluyen aquí la asistencia segregada del resto de pacientes, a los pacientes contagiosos, como medio de protección al resto de ellos, que estando enfermos, no están infectados.

Veremos en este tercer escenario, cómo la respuesta sanitaria, lejos de suponer un alivio del problema, puede agravarlo si esta no se adopta con la debida determinación y rigor.

Las curvas epidémicas son regresiones logísticas que llegado a un límite, más allá del cual la epidemia no puede crecer por agotamiento de los susceptibles, con la respuesta sanitaria y, sobre todo, con las dudas políticas en su aplicación, generan las denominadas olas de contagio, dado que, la respuesta sanitaria, rompe el devenir normal de la epidemia, pero no consigue eliminar el peligro, sino sólo frenar su avance.

Figura 5 

Modelo formal

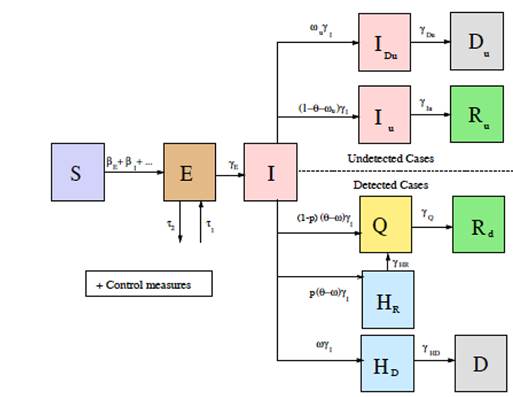
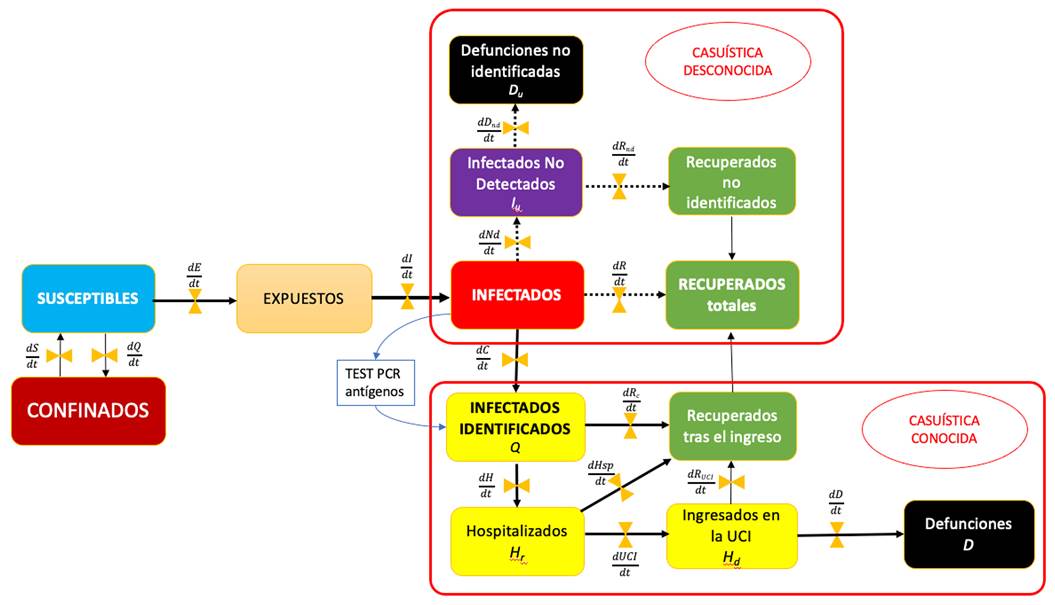
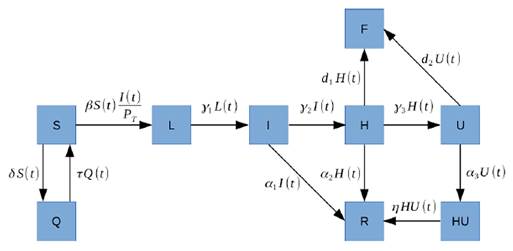
El modelo formal, resultado de este proceso intelectual, es el modelo matemático denominado Modelo de Epidemias por Dinámica de Sistemas (MEDS), representado esquemáticamente en la figura 6.

Figura 6 

Este modelo muestra una secuencia dinámica principal que la componen los colectivos humanos del modelo SIR (SUSCEPTIBLES, INFECTADOS Y RECUPERADOS) más el colectivo de EXPUESTOS, que se hallan en fase de incubación de la enfermedad.

En la parte inferior, se describe la secuencia asistencial, donde se despliegan los colectivos humanos diagnosticados, hospitalizados (en planta y en UCI, y finalmente los fallecidos). En realidad, lo que conocemos de la epidemia, lo aportan los enfermos detectados, bien por que en ellos aparece sintomatología compatible, o identificados por los test masivos de PCR y antígenos que se están haciendo a la población. Es la ZONA CONOCIDA de la epidemia, y la que podemos controlar, bien por cuarentena domiciliaria o ingreso hospitalario.

Una tercera secuencia, en la parte superior, la forma el colectivo de infectados no detectados (NoDet). Este es el colectivo realmente problemático, porque en realidad, lo que se conoce de la pandemia es realmente el colectivo diagnosticado y asistido, pero el que realmente contagia y mantiene la expansión de la epidemia es el colectivo de infectados no identificados, y que es la gran amenaza fantasma que se cierne sobre la población, razón por la que la única forma de controlar la epidemia es el cribado masivo de los susceptibles, al menos hasta que sea efectiva alguna de las vacunas que parecen estar en la línea de salida para ser distribuidas por el mundo.

Matemáticamente, las variables de nivel se resuelven con integrales y las variables de flujo, con ecuaciones diferenciales .

El comportamiento del modelo, se ha ensayado en el caso de la población de la Comunidad de Madrid, utilizando como serie temporal la información aportada por el Instituto de Salud Carlos III¹⁸, recogidos por la web x-y.es/COVID19¹⁹.

Según los datos difundidos por el Instituto de Salud Carlos III correspondientes al 17/11/2020 en C. Madrid ha habido un total acumulado de 339.610 casos: 297.554 detectados por prueba PCR, 22 vía test de anticuerpos y 42.034 por otras vías; y alcanza las 11.040 defunciones.

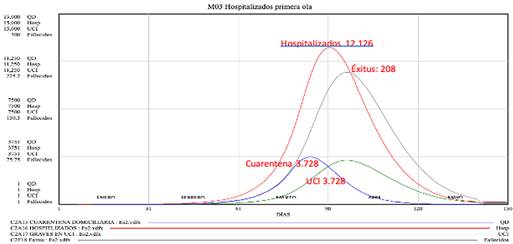
La simulación ajustada a los datos reales en la primera ola se muestra en la tabla 1 o cuadro de mando del modelo.

Tabla 1 Cuadro de mando de las tasas del modelo. 

m Contactos x contagiado	3	Tasa de asintomaticos inf.	0,44	Tasa de ingreso en UCI	0,05
t Probabilidad de contagio	0,693	Tasa recuperacion NoDet	0,6	Dias Est Media UCI	10
Tiempo de incubación	7	Tasa mortalidad NoDet	0,15	Tasa de fallecidos en UCI	0,06
g Dias de contagiosidad	20	Dias de cuarentena	14	Tasa de reinfección	0
Tasa de cuarentena	0,2892	Tasa de ingreso en hospital	0,5	Tasa de vacunación	0
Tasa de NoDetectados	0,285	Dias Est. Media hospital	14	Tasa de PCR positivos	0,6

RESULTADOS

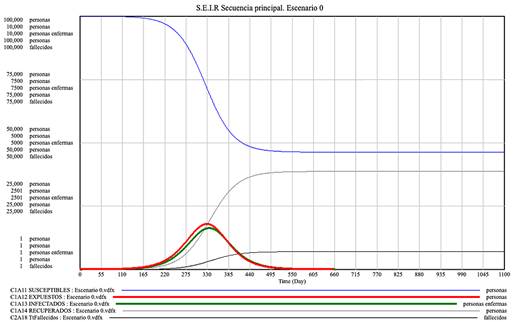
El modelo se ha ensayado en condiciones genéricas, sobre una hipotética población de 100.000 personas, para simular el «comportamiento inercial» de la epidemia, es decir, aquel por el que esta se expande sin intervención sanitaria. El resultado, basado en una tasa de contagio de 2 casos por infectado y 0,15 como probabilidad, da como resultado 53.600 casos, es decir el 46% de la población de 100.000.

Figura 7 

Figura 8 

La tabla 2 expresa los datos principales reales y en números rojos, los casos arrojados en la simulación (entre paréntesis se indica los casos acumulados).

Tabla 2 

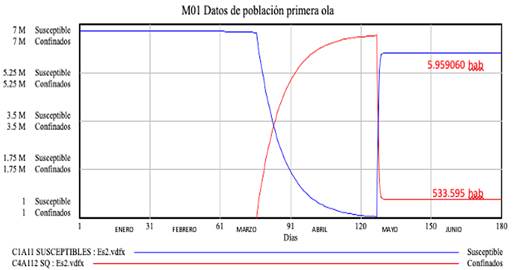
Según el Real Decreto 463/2020, de 14 de marzo, la noche del 15 de marzo se ordenó el confinamiento total de la población, excepto los servicios esenciales. Este hecho se simula, según se ve en la figura 9, mediante un brusco descenso de los susceptibles y un incremento súbito de la variable de nivel de personas confinadas.

Figura 9 

Para ello, a la variable Confinados, que calcula el número de personas confinadas por UdT, se la introduce un motor de inferencia (IF THEN) de modo que si el momento de la simulación es mayor que un valor introducido ex profeso para indicar cuándo el modelo ha de simular el confinamiento, entonces, la variable de flujo Confinados, pasa de ser «0» a un valor predefinido, que se ha estimado en 0,8 (confinar el 80% de la población) exceptuando los servicios esenciales. El resultado es el de la figura 9.

Y tal día como el 5 de mayo, cuando comenzó el proceso de desescalada, se vuelve a recuperar la vida normal.

Según esta actuación, las curvas de incidencia calculadas son las que representa las figuras 10 y 11, con un pico de 5.174 infectados por UdT, y una incidencia diaria de 3.696 nuevos casos el 20 de marzo.

Figura 10 

Figura 11 

Obligadamente, se ha tenido en cuenta el problema de los asintomáticos, definidos en el modelo como No Detectados, y que se ha estimado hipotéticamente en 2081 como pico máximo de la primera ola.

Así las cosas, se afronta realmente el verano, con una incidencia de casos diarios reales de entre 21 y 91 casos, con un promedio de 55,18 casos diarios entre el 13 de junio y el 12 de julio, con un promedio de 57 casos diarios. Fueron fechas de alegría y esperanza, ante lo que parecía el fin de la pandemia, con clamores gubernamentales de «haber vencido al virus». Y con la ineludible necesidad de recuperar la economía, sobre todo la hostelería y el turismo, se permitió que la gente «tendiera a hacer una vida normal». Sin embargo, nada más lejos de la realidad.

En este gráfico (Figura 10) se muestra la evolución real, (datos del ISCIII) tras el fin del desconfinamiento. Se puede decir que hubo tregua entre el 15 de junio y el 15 de julio, ya que a partir de entonces todo fue a peor, como todos conocemos

Poder simular este escenario, es francamente complejo, dado que es imposible aplicar al modelo un «comportamiento caótico», conocido como «el martillo y la danza», el martillo es la medida dura (confinamiento) y la danza son las medidas «soft» de limitaciones a la movilidad esporádicas, medidas higiénicas, el uso de mascarillas, etc…, a no ser que se le estén introduciendo reiteradamente instrucciones condicionales, que rompan cualquier tipo de evolución predecible mediante modelos matemáticos coherentes. Y esto es lo que se ha tenido que hacer.

Para poder ajustar la simulación a los casos reales, se ha tenido que «forzar» al modelo a «no seguir» el normal desarrollo de los acontecimientos, basados en las ecuaciones diferenciales e integrales, sino en responder en determinados momentos de la simulación a sentencias condicionales tipo «if then else», variando así el rumbo de los acontecimientos, que es lo que las medidas, tanto sanitarias como sociales, pretenden.

Figura 12 

Figura 13 

Un indicador muy elocuente de la evolución ha sido el número de reposición (Re) que, salvo en el periodo veraniego, el modelo indica que jamás ha estado por debajo de 1.

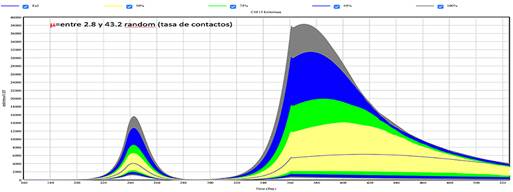
Por último, para tratar de minorar la dispersión de ajuste entre los datos reales y simulados, se ha aplicado el análisis estocástico mediante el método de simulación Montecarlo (200 iteraciones), con un resultado que ofrece este aspecto.

Figura 14 

En suma, con los datos disponibles y el comportamiento de la epidemia, este modelo y, en opinión del autor, cualquier otro, más de pretender ajustarse a los datos reales, que vemos no obedecen a la lógica, es advertir que «hay que tratar de evitar en lo posible detener el avance», porque puede ser demoledor… siempre que los datos disponibles respondan a la realidad, es decir, tratar de reducir al máximo la casuística NO DETECTADA».

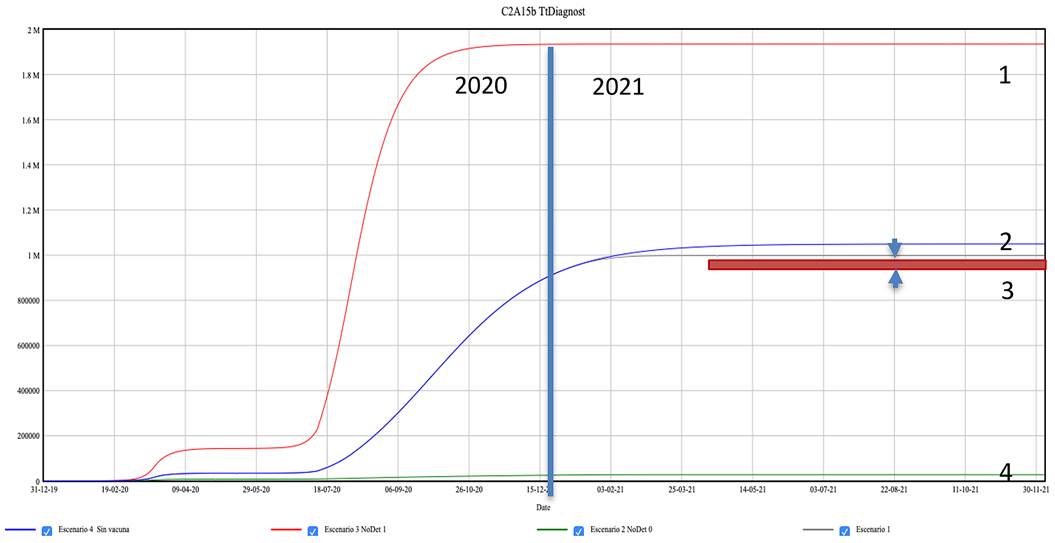
Y una segunda advertencia es la que surge de cómo de comportará la pandemia en 2021.

Esta gráfica plantea un serio dilema:

Figura 15 

La línea superior «1», (roja) plantea el escenario en el que todos los asintomáticos, no detectados o portadores sanos, sean contagiosos. Supone que el total de diagnosticados a final de 2021 podrían suponer casi dos millones de personas (Comunidad de Madrid).

La línea «2» (azul), plantea el escenario que ha simulado el modelo en 2020, con sus dos olas y una proporción de asintomáticos del 47% casi el doble de los detectados, sin la aplicación de la vacuna.

La línea «3» (gris), plantea el mismo escenario de la línea 2, pero aplicando la vacuna. La diferencia de casuística entre ambos escenarios resulta ridícula, de 998.000 diagnosticados sin vacunar a 930.000 vacunados.

Sorprendente.

DISCUSIÓN

Que el autor conozca, no se ha elaborado un modelo de simulación dinámica para el ámbito de la comunidad de Madrid, aunque sí para otras zonas, como es el trabajo del equipo de Ángel Manuel Ramos de la Fad. de Matemáticas de la Universidad Complutense (Ref. 3). Este es un modelo analítico θ-SIR, basado en los mismos principios que el modelo SIR de Kermack y McKendrick, pero extendido, como el MEDS a pacientes infectados no detectados.

Figura 16 

Los resultados de este modelo pueden ser tan ajustados como se quiera, de la misma forma que MEDS, porque en ambos casos, los modelos reflejan comportamientos inerciales que son los que se consigue con la aplicación de las ecuaciones. Pero en el caso de esta pandemia de COVID, se ha procedido por los gobiernos a tantas medidas tanto correctas como incorrectas para frenar la propagación del virus que, sólo introduciendo excepciones en el modelo, las curvas inerciales pueden ajustarse al caos observado en el comportamiento real. Esto es inevitable.

Otro modelo para COVID19 es el desarrollado por el equipo de la Universidad de Valencia (Ref. 4), con un esquema similar donde incluye a los confinados; exponen las tasas de calibración, pero no arrojan ningún resultado, al menos en el trabajo de 2 de abril, al inicio de la pandemia.

Figura 17 

El resultado que arroja el modelo MEDS, es a juicio del autor, en esencia similar que el que arrojan los demás modelos, pero se significa que todos presentan, a juicio del autor, tres problemas básicos.

El primero es respecto de los límites: ¿Dónde termina el modelo? ¿Que variables pertenecen a él y cuáles no? La respuesta parece clara, en el núcleo del modelo MEDS, de este trabajo, están descritas todas las variables, pero incluso estas son difusas, en el sentido de que el comportamiento de cada variable de nivel tiene un comportamiento variable según se desagreguen por grupos de población, por ejemplo por grupos de edad, jóvenes, adultos y mayores, están siendo en la realidad, tres grupos de edad de comportamiento significativamente diferente. Sin embargo, en el modelo están unidos dentro de las mismas variables. Esto es fuente de una importante variabilidad en las tasas, que se muestra en el análisis estocástico.

El segundo de los grandes problemas es el calibrado. Sin haber hallado una metodología sencilla para su calibración, se entiende que una propiedad que han de tener los modelos es su «elegancia matemática», es decir, la tentativa de conseguir con el simple diseño de modelos analíticos, que ellos respondan al comportamiento real.

Dinámica de Sistemas ofrece muchas posibilidades de truncar esa elegancia inercial, mediante sentencias que introducen la lógica de los motores de inferencia, con sentencias del tipo «sí… entonces» (IF THEN ELSE), es decir, si se cumple tal circunstancia, entonces hacer «A» y si no, «hacer B». En esta primera versión del modelo, así se ha procedido.

El tercero de los problemas es la fiabilidad de los datos. Sin ánimo de entrar en el incómodo problema del negacionismo, sí que es cierto que, dado que este episodio pandémico se está desarrollando en nuestra actual sociedad de la información, ha de tenerse en cuenta que no sólo se está viviendo una pandemia biológica, provocada por un virus hasta ahora desconocido, sino además se está viviendo una «infodemia»²⁰, una pandemia informativa, que no hace más que incrementar o disminuir la realidad, según conviene a las autoridades políticas y sanitarias. Esta es una pandemia que llega y se difunde mucho antes que la real, debido al efecto amplificador de los canales de información.

Hay indicios razonables para pensar que los datos que se vierten no son precisamente los reales y que los casos reales, según se mire, pueden ser mucho mayores o menores, según de fiable sea el sistema de información epidemiológico, su homogeneidad respecto de las zonas, ciudades, regiones, CCAA o países. No hay seguridad de que los datos de Francia obedezcan al mismo criterio que los españoles o los japoneses. Pero el factor más importante para la falta de fiabilidad es el colectivo de «No detectados». Así que tanto más cribado por PCR se efectúa, más infecciones se registrará, e inversamente, cuanto menos test se hagan, menos infecciones se registran.

El modelo plantea un serio problema de orden de magnitud. A finales de diciembre, Madrid, Comunidad alcanzaba los 400.000 afectados confirmados mientras que el modelo predice el doble. Y la evolución de 2021, plantea el típico comportamiento de una epidemia que se agota por haber alcanzado la inmunidad colectiva.

Sin embargo estamos viendo que con la aparición de la Cepa Británica y el incremento de la casuística en torno a las navidades, lo más probable es que se produzca una tercera ola más importante aún que la segunda y que, la efectividad de las vacunas de Pfizer y Moderna, no sean al final igualmente efectiva al mismo nivel. En otras palabras, que si bien los modelos pueden reproducir lo sucedido (adulterando las ecuaciones con instrucciones directas en determinados tiempos t = i, j, k…), la prospectiva es demasiado arriesgada debido a la imprevisibilidad de los acontecimientos. ¿Qué utilidad tienen los modelos entonces? A juicio del autor, bastante para comprender el comportamiento dinámico, la complejidad dinámica del proceso, pero bastante poca para predecir el caos en que se está convirtiendo la situación.

En otras palabras, los modelos matemáticos tienen para esta pandemia un valor descriptivo y explicativo, pero escaso valor prospectivo.

No obstante, este tipo de modelo, si se asocia a un Sistema de Mando y Control Sanitario (diseñado bajo los mismos principios de un SMCM (C2), Mando y Control Militar, puede contribuir a una mejor gestión de la epidemia, al menos en zonas localizadas, como es el caso de una Comunidad Autónoma.

CONCLUSIONES

ADDENDUM

Este modelo fue desarrollado con un horizonte temporal en el día 11 de diciembre de 2020, con los datos disponibles hasta esa fecha. Más allá de esa fecha, la simulación era eminentemente prospectiva. Desde entonces hasta la actualidad (1 de febrero de 2021, momento de escribir este addendum) han sucedido y están sucediendo muchos acontecimientos, fundamentalmente: 1) la aparición de las nuevas cepas, la británica y en los últimos días la sudafricana, 2) el proceso de vacunación en masa y 3) el crecimiento nuevamente exponencial de la tercera ola que se encuentra en estos momentos en España y en el mundo en el clímax, lo que está obligando a los gobiernos (en España, Central y autonómicos) a tomar medidas perfectamente heterogéneas, al borde de nuevos confinamientos totales.

En relación con las nuevas cepas, éstas suponen una bifurcación en la prospectiva del modelo, que dispara múltiples posibilidades de evolución, dependiendo de que la población ya inmunizada lo sea también a éstas o no. Tampoco está claro, a día de hoy, que las nuevas vacunas RNAm puedan ser útiles para proteger ante estas nuevas variantes del virus. Por otra parte se está desvaneciendo cada día que pasa la posibilidad de alcanzar un 70% de vacunados en julio, y con ello la ansiada inmunidad colectiva, debido a la falta de compromiso de las farmacéuticas y por los problemas logísticos de distribución hasta los puntos finales de dispensación.

Y por último tenemos la gran protagonista de todo esto, que no es el virus, sino la COMPLEJIDAD DINÁMICA, que como bien define Klaus Schwab en su libro «COVID-19: el Gran Reinicio»: «En lo más profundo de nuestro ser, notamos que cuanto más complejo es un sistema, mayor probabilidad hay de que algo salga mal». Y están saliendo y saldrán muchas cosas mal, y de entre todas, la variable independiente que marca los tiempos, medidas y las decisiones, la saturación del sistema sanitario, definida por el número de camas de UCI con capacidad de ventilación mecánica, y muy de cerca por la disponibilidad de personal de enfermería cualificado en cuidados críticos. Y añade Schwab algo que muchos hemos pensado erróneamente, que COVID19 no es un suceso Cisne negro, sino Cisne blanco, porque era previsible que esta catástrofe comparable con la Segunda Guerra Mundial ocurriera, pero que encierra infinidad de sucesos Cisne negro, en referencia a todas las repercusiones en todos los ámbitos de la vida , personal, familiar, comunitaria, social e internacional, que las harán añicos, y que ya se empieza a hablar de que COVID19 ha marcado ya un punto de inflexión en la Historia de la Humanidad, un «la Historia aC y la Historia dC» (Antes del COVID y después del COVID).

Los modelos matemáticos servirán para encontrar un poco de sentido y lógica a lo que está pasando, sin ánimo de predecir lo que es está convirtiendo a pasos agigantados en un descomunal atractor caótico.