Introducción
La mortalidad es teóricamente el resultado más sencillo de medir y él más relevante para evaluar el efecto de nuestra intervención sobre una población de pacientes con enfermedad renal crónica1. Son muchas las publicaciones que comparan la supervivencia entre las distintas etapas de la enfermedad2, etiologías, técnicas de terapia renal sustitutiva (TRS) (3-12 o entre grupos y países13,14. Sin embargo, existe cierta controversia y disparidad de resultados en las publicaciones y esto se debe en parte a la falta de homogeneidad en las definiciones de caso, los enfoques de análisis estadísticos, el manejo de los pacientes censurados y las formas de descripción y presentación de resultados15,16. Por ello, los diferentes registros de pacientes con enfermedad renal crónica en TRS han intentado definir un modelo que resuma las distintas formas de medir la mortalidad17, sin haber llegado a un modelo de consenso. Ello facilitaría la comparación entre los distintos grupos de trabajo sobre un tema tan relevante como la mortalidad de los pacientes que reciben TRS y, más en concreto, diálisis peritoneal (DP). Con esta intención se orienta nuestro análisis, que aplica los diferentes métodos sobre una misma base de datos (BD), lo que nos permite compararlos y establecer una discusión metodológica sobre el tema, intentando avanzar en nuestro conocimiento y facilitar la comprensión de la información disponible en este campo.
Material y métodos
El Grupo Centro de Diálisis Peritoneal (GCDP) presenta un análisis descriptivo sobre la BD que hemos generado con una recogida prospectiva de datos desde 2003, según se describe en publicaciones previas18. Se han analizado datos de 1.890 pacientes incidentes en DP pertenecientes a 22 centros, agrupados en el territorio de las comunidades de Madrid, Castilla-León, Castilla-La Mancha, Extremadura y Aragón.
La información es recogida en una DB anónima, con un diseño, manejo y análisis aprobado por un comité científico e independiente de las compañías que dan soporte al proyecto. Los pacientes dan su consentimiento a la inclusión al entrar en DP. El análisis estadístico se lleva a cabo mediante SPSS v. 15.0 y STATA v12 para análisis de RC.
Realizamos un primer análisis descriptivo de la población en la línea de lo previamente publicado18. La segunda parte del análisis se enfoca al cálculo de la mortalidad en los últimos 7 años (2007-2013) aplicando la metodología referida por los distintos grupos y registros autonómicos, nacional e internacionales (ver tabla 1) para compararlos entre sí y evaluar los motivos de disparidad.
Tabla 1 Registros y cálculo de mortalidad
| Registro | Cálculo de tasas | Curvas de supervivencia |
|---|---|---|
| REER (España) | Fallecido en año natural/prevalentes a fin de año | KM desde 2012 (con aquellas autonomías que aportan datos individuales). Según 1.er TRS por intención de tratar (los cambios de TRS no son pérdidas) |
| RMRC (Cataluña) | Fallecido en año natural/prevalentes a fin de año (modelo REER) | Supervivencia actuarial y gráficos KM. Según 1.er TRS, cambios de TRS son pérdidas |
| REMER (Madrid) | Fallecidos año/prevalentes a fin de año+fallecimiento | KM desde 2008. Según 1.er TRS, cambios de TRS son pérdidas |
| SICATA (Andalucía) | Fallecidos año/(prevalentes a fin de año+½ fallecimiento) | Supervivencia actuarial y KM. Según 1.er TRS, los muertos en 2 meses tras cambio de técnica de diálisis, se asignan al 1.ertratamiento, resto son pérdidas en 1ª técnica y reinicio en la nueva |
| ERA-EDTA (Europa) | Fallecido en año natural/prevalentes a fin de año (modelo REER) | KM. Solo TRS desde día 91. Según 1.er TRS, cambios de TRS son pérdidas |
| RDPLF (Francia) | No define en su publicación | Supervivencia actuarial y KM Por intención de tratar (cambio DP a HD se mantiene en DP para análisis y TX es pérdida de seguimiento) |
| USRDS (EE. UU.) | Fallecido en año natural/prevalentes a fin de año Solo incluye pacientes con>90 días en TRS | Supervivencia actuarial y KM. Solo TRS desde día 91. Según 1.erTRS, cambios de TRS son pérdidas |
| ANZDATA (Australia y Nueva Zelanda) | Fallecido en año natural/prevalentes a fin de año (modelo REER) | KM. Según 1.er TRS, cambios de TRS son pérdidas |
DP: diálisis peritoneal; HD: hemodiálisis; KM: método de supervivencia por curvas de Kaplan-Meier; TRS: tratamiento renal sustitutivo; TX: trasplante
A continuación, se exponen los principales métodos para calcular la mortalidad de una población, describiendo sus ventajas e inconvenientes.
Densidad de mortalidad
Se calcula como el número de fallecidos en un año (generalmente año natural) dividido por la suma total del tiempo en riesgo. Cada paciente aporta su tiempo de seguimiento durante el año. Por ejemplo, un paciente que no fallece durante el año y comienza el 1 de julio aporta 6 meses y un paciente que seguimos 6 meses hasta que se traslada y luego se pierde el seguimiento aporta igualmente ese tiempo. Los datos se expresan en fallecidos por años-paciente. Por ejemplo, 10 fallecidos en un grupo que acumule 200 años paciente en riesgo, se pueden expresar como: 0,05 fallecidos/año-paciente o 5 fallecidos/100 años-paciente, que se reduce a un 5% por año en riesgo. Con este método se esta expresando una densidad de mortalidad durante el periodo temporal. La validez de la estimación depende claramente del número de pacientes de seguimiento perdidos y que estos se distribuyan aleatoriamente, con igual riesgo que aquellos que persisten en la base de datos.
Mortalidad
Este índice se calcula como el número de fallecidos durante el año (habitualmente natural) divido por los pacientes en riesgo. Algunos registros asumen que la prevalencia de pacientes es estable durante un año y la media es muy similar a la de un día cualquiera (por ejemplo, el último del año). Por ello se calcula dividiendo todos los muertos durante el año por la prevalencia puntual a final del año. Esta aproximación es la utilizada por el registro catalán19, entre otros, y es más precisa para poblaciones grandes con pocas fluctuaciones y mortalidad baja, como en estudios de población general. Otros registros utilizan fórmulas parecidas para estimar los pacientes en riesgo, sumando los pacientes fallecidos en el denominador (caso del REMER) (20, o calculando la prevalencia media del periodo, es decir la media de pacientes al inicio y final de cada año (registro andaluz) (21.
Supervivencia actuarial
Calcula la probabilidad de supervivencia en cada año contando a partir del inicio de DP. Agrupa el tiempo de seguimiento de cada paciente en intervalos predeterminados (generalmente anuales) y calcula la probabilidad de supervivencia como la probabilidad condicionada correspondiente a cada intervalo de tiempo. Con este método también podemos calcular la tasa relativa media de incidencias por año (por ejemplo a los 8 años de seguimiento). Este método es el utilizado por el registro francés de DP (RDPLF) (22.
Probabilidad de supervivencia Kaplan-Meier
Calcula la probabilidad acumulada de supervivencia a lo largo de un seguimiento dado. El modelo trabaja con la variable dicotómica: evento muerte o libre de evento al final del seguimiento. Se considera perdido de seguimiento a aquel cuyo seguimiento se interrumpe por otro motivo: trasplante, paso a hemodiálisis (HD), traslados o recuperación de función renal. Estos pacientes aportan su seguimiento hasta el último evento de un paciente previo a su pérdida de seguimiento y posteriormente se eliminan del análisis. Es el modelo utilizado por el registro EDTA23 y por el registro francés de enfermedad renal (REIN)24, entre otros. En 2012 el REER ha comenzado a presentar este tipo de análisis con la agrupación de varios registros autonómicos que comparten su información de datos individuales. En caso de cambio de HD a DP o viceversa, el registro andaluz asigna la muerte a la primera técnica si se produce en los primeros 2 meses tras el cambio21. La mediana del tiempo es el índice más utilizado y se corresponde con el tiempo en el cual la probabilidad de supervivencia es del 50% o menor. Este método tiene unas condiciones de aplicación, como asumir que el riesgo es constante a lo largo del tiempo, algo que no siempre es cierto. La calidad de la estimación depende de que las pérdidas de seguimiento sean bajas, de que su distribución sea uniforme a lo largo del tiempo y de que sean independientes del evento de interés.
Algunos estudios presentan la curva de mortalidad acumulada que es la complementaria de la de supervivencia.
Modelo de decrementos múltiples para evaluar riesgos competitivos (RC)
Estima la probabilidad de supervivencia teniendo en cuenta los posibles eventos competitivos (EC). En este análisis consideraremos como EC la recuperación de función renal, el trasplante y el paso a HD, porque estas situaciones modifican la probabilidad de supervivencia. En general, el pronóstico es mejor en trasplantados que en HD. El modelo trabaja con 2 tipos de eventos, el evento principal (fallecidos) y los competitivos (salidas por TX, HD o recuperación de función renal). El resto de pacientes que no completan su seguimiento se consideran perdidos. Este modelo asume que las diferentes salidas son independientes entre sí. El análisis se presenta como 2 curvas de eventos acumulados, una para los eventos competitivos y otra para la mortalidad.
Resultados
Se incluye a 1.890 pacientes con un tiempo de seguimiento total de 3.633,8 años, con un seguimiento medio de 1,92 años/paciente (rango: de 1 mes a 10,5 años). Al finalizar el seguimiento, 261 fallecen (13,8%), 380 pasan a HD (20,1%), 682 reciben un trasplante renal (36,1%), 40 recuperan la función renal (2,1%). Se ha perdido el seguimiento de 34 pacientes por traslado a otros centros externos al GCDP (1,8%). Por último, 493 pacientes restantes continúan en DP (26,1%).
El análisis descriptivo de la población se resume en la tabla 2, donde se comparan las características de los distintos grupos de pacientes clasificados por la situación al final del seguimiento. La edad, distribución por sexo y comorbilidad asociada a índice de Charlson, diabetes mellitus y eventos cardiovasculares previos a inicio de DP y función renal residual se muestran en la tabla.
Tabla 2 Descripción de la población según tipo de salida
| Sigue en DP | Fallecimiento | Paso a HD | Trasplante | Recupera FR | Traslado | Total | |
|---|---|---|---|---|---|---|---|
| N (%) | 493 (26,1) | 261 (13,8) | 380 (20,1) | 682 (36,1) | 40 (2,1) | 34 (1,8) | 1.890 |
| FRR media y (DE) (ml/min) | 7,2 (4,1) | 6,2 (4,7) | 6,3 (4,5) | 7,2 (4) | 11 (4,2) | 5,9 (4) | 7,0 (4,4) |
| Edad media y (DE) en años | 56,7 (15) | 65,4 (13,5) | 57,7 (16,6) | 49,1 (13,3) | 55,2 (18,2) | 51,2 (16,7) | 55,0 (15,6) |
| % CV | 23,0 | 55,9 | 32,5 | 10 | 30,8 | 23,5 | 25,1 |
| % DM | 25,7 | 42,5 | 30,2 | 15 | 23,1 | 26,5 | 25,0 |
| % Varones | 63,5 | 64,0 | 65,1 | 65,1 | 59,0 | 47,1 | 64,2 |
| Índice de Charlson mediana y [rango intercuartílico] | 3 [2-4] | 2 [2-3] | 3 [2-5] | 4 [3-6] | 3 [2-4] | 2,5 [2-4] | 3 [2-4] |
CV: eventos cardiovasculares; DE: desviación estándar; DM: diabetes mellitus; FRR: función renal residual
Se analiza una población incidente desde 2003, por lo que en los primeros años existe una tasa de mortalidad muy baja al compararla con la de prevalentes, obteniendo datos sesgados de mortalidad. Por ello, se decide realizar el análisis de mortalidad desde el año 2007 hasta el 2013, ambos inclusive, cuando las proporciones se han equilibrado.
En la tabla 3 se contabilizan los fallecimientos y prevalentes al final del año, el tiempo acumulado y las tasas de mortalidad y letalidad, según los diferentes métodos revisados.
Tabla 3 Tasas y porcentajes
| 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | |
|---|---|---|---|---|---|---|---|
| Fallecimiento (n) | 36 | 35 | 37 | 28 | 33 | 20 | 30 |
| Prevalentes a final de año (n) | 405 | 385 | 399 | 421 | 385 | 313 | 245 |
| Σ pacientes-año | 406,4 | 406,4 | 396,2 | 422,8 | 416,5 | 383,3 | 264,1 |
| Núm. de fallecimiento/ 100 pacientes-año | 8,9 | 8,6 | 9,3 | 6,6 | 7,9 | 5,2 | 11,4 |
| % de fallecidos/prevalentes | 8,9 | 9,1 | 9,3 | 6,7 | 8,6 | 6,4 | 12,2 |
| % de fallecidos(prevalentes + fallecidos) | 8,2 | 8,3 | 8,5 | 6,2 | 7,9 | 6,0 | 10,9 |
En el análisis de mortalidad mediante el método de KM (fig. 1A) la mediana de supervivencia es de 6,4 años (IC 95%: 5,9-7,0).
En la figura 1B se exponen los resultados obtenidos al utilizar el método de decrementos múltiples, que calcula el análisis de mortalidad evaluando los riesgos competitivos (paso a HD, trasplante, recuperación de la función renal).
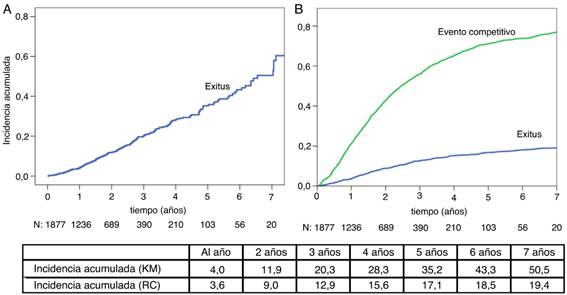
Figura 1 A) Incidencia acumulada calculada según método de Kaplan Meier. B) Incidencia. acumulada de mortalidad calculada con el método de decrementos múltiples. Se indica en el pie de la figura el número de pacientes en riesgo. Se muestra en la tabla la mortalidad acumulada por ambos métodos.
Al comparar ambos métodos (KM vs. RC), observamos como la mortalidad acumulada es similar en el primer año. En el análisis con KM este porcentaje aumenta más rápidamente que en el modelo de RC, sobrestimando de este modo la mortalidad.
Discusión
Nuestro artículo pretende resaltar la disparidad de resultados que se obtienen con diferentes métodos de análisis de mortalidad en DP25. Cada método es correcto en sí mismo y trata de reflejar la mortalidad, pero no expresa lo mismo y trasmite diferente impresión al lector, dificultando la comparación entre publicaciones. Realizar estos análisis sobre una misma BD, sólida y contrastada, ayuda a comprender los detalles metodológicos de estas diferencias. Por ejemplo, las tasas del año 2012 varían entre un 5,2 y un 6,4% según el método, lo que representa una diferencia relativa superior al 20%.
En los análisis realizados por nuestro grupo durante 10 años, se encontraban diferencias en la estimación de las distintas tasas de mortalidad en los primeros años, ya que predominan los pacientes incidentes sobre los prevalentes20,21. Esta diferencia desaparece a partir de 2006, y las tasas se mantienen estables al perderse el efecto de mayor supervivencia inicial de los incidentes20,21.
Existen una serie de limitaciones en la forma de calcular la tasa de letalidad como hace el REER26. Este registro asume que la población en riesgo es constante durante todo el tiempo de seguimiento y, por tanto, es la misma el último día del año que en su promedio. Esto puede no ser así en programas en crecimiento o descenso, y genera más error cuanto más pequeña es la muestra y mayor la proporción de fallecidos. También puede verse muy afectada por tasas de trasplante elevadas (como sucede en la autonomía madrileña). Por ello, no nos parece una buena forma de calcular mortalidad, especialmente en muestras pequeñas como la de un determinado servicio de nefrología, donde puede haber fluctuaciones excesivas en años consecutivos. Nuestra recomendación es calcular el tiempo real en riesgo de cada paciente y reducir así a tasa por año-paciente.
El análisis de mortalidad mediante KM es más completo y descriptivo, pero no podemos olvidar que deberían cumplirse las condiciones de aplicación del método. El riesgo de muerte de nuestros pacientes tiende a ser menor al principio y el modelo exige que este riesgo sea uniforme a lo largo del tiempo en DP. Además, existe un porcentaje de salidas de DP con paciente vivo muy importante. Por ejemplo, en nuestro estudio y tras 10 años de seguimiento, la proporción de pacientes que se consideran perdidos (TX, paso a HD, recuperación de función renal) cuadruplica a los pacientes fallecidos (1.162 vs. 261). La mayoría de registros reportan un reparto de las salidas de DP en 3 tercios casi iguales para fallecimiento, trasplante y cambio a HD25. Sin embargo, en nuestro grupo, los TX representan más del 50% del total de las salidas de programa de DP. Al final de nuestro seguimiento más de la mitad de nuestros pacientes son pérdidas de seguimiento, sin alcanzar el evento muerte. Por ello, el análisis de Kaplan-Meier puede dar una impresión poco ajustada a la realidad.
El modelo de RC aquí propuesto analiza de forma diferente estas situaciones y refleja mejor lo que está sucediendo con nuestros pacientes. En este modelo esos pacientes perdidos se diferencian según su salida (TX, HD, recuperación de función renal) estableciendo cada una de ellas como un evento independiente que compite con el resto. Así, lo esperable es que los pacientes trasplantados tuvieran menos riesgo vital que los que salen a HD, lo que puede explicar de este modo las diferencias en la relación TX/HD entre los análisis utilizando KM o RC.
A pesar de ser el modelo más ajustado desde nuestro punto de vista, también existen una serie de limitaciones en el análisis realizado. La primera de ellas es la falta de seguimiento cuando el paciente abandona la técnica, sin poder determinar cuál es la evolución de cada uno de ellos. Por ejemplo, hay situaciones en que determinados pacientes en fase terminal se trasfieren a HD y fallecen pocas semanas o meses después. Otra limitación es el tiempo real en la técnica que aporta cada uno de los pacientes en los datos analizados. El tiempo medio en la técnica por paciente es demasiado corto (aproximadamente 2 años) y permanece estable después de 10 años de funcionamiento de la BD. Como ya se ha publicado en otros artículos de nuestro grupo, este breve tiempo de seguimiento es consecuencia de la alta tasa de salidas a TX en una población que, por sus características demográficas y su privilegiada situación clínica, accede con mayor rapidez a un trasplante renal como TRS definitivo27.
Por último, debemos considerar otros factores que influyen en la diferente mortalidad en DP de cada registro28. Aspectos como la política de asignación/elección del primer TRS pueden influir en el diferente perfil de los pacientes en cada técnica. Modelos de asignación obligatoria (por ejemplo, modelo Hong-Kong) o de asignación prioritaria (modelo PD-first) se comportan de diferente manera que el nuestro de libre elección29. En el modelo español, se constata una tasa de inclusión en DP en torno al 15% y una selección positiva de pacientes más jóvenes y con menor morbilidad para esta técnica. También debemos considerar las características generales de la población, con diferentes edades o prevalencias de obesidad y diabetes mellitus, algo muy relevante al comparar con registros como el norteamericano. Por último, registros como el norteamericano excluyen a los pacientes que no sobreviven a los primeros 90 días de tratamiento, haciendo imposible la comparación con nuestros resultados. La aplicabilidad en nuestro entorno del análisis de otros grupos o registros depende de estos factores que condicionan la validez externa del trabajo publicado.
La BD del GCDP se rellena de forma prospectiva por los clínicos directamente responsables del seguimiento del paciente, lo que asegura una mayor precisión que la de los formularios administrativos empleados en otros registros.
Conclusión
La mortalidad real de una población determinada podría parecer sobre- o infraestimada en función del método elegido para analizarla y presentarla. El presente análisis, utilizando diferentes métodos sobre la misma BD, ayuda a comprender estas diferencias. Finalmente parece razonable, dada la disparidad de fórmulas, establecer un método compartido por todos los registros para estandarizar un sistema unívoco y establecer comparaciones internacionales. El modelo de RC resulta conveniente en situaciones de alta proporción de pérdida de seguimiento.