TEMAS PARA RESIDENTES 

Pruebas de significación en Bioestadística 

S. Gómez-Biedma, M. Vivó, E. Soria 

Servicio de Biopatología Clínica. Hospital La Fe. Valencia. 

Palabras clave: Bioestadística, Parámetros estadísticos, Pruebas de significación. 

Key Words: Biostatistic, Statistic parameters, Signification tests

---

Recibido: 9-XI-00
Aceptado: 29-III-01

Correspondencia: Simón Gómez-Biedma Gutiérrez.
Departamento de Biopatología Clínica.
Hospital La Fe. Avenida Campanar, 21.
46009. Valencia

Introducción 
Las pruebas de significación estadística sirven para comparar variables entre distintas muestras. Si la distribución de la muestra es normal se aplican los llamados tests paramétricos. Si la distribución no puede asumirse normal se aplican las pruebas no paramétricas. Hay que tener siempre en cuenta que los tests paramétricos son más potentes y dan más información que los no paramétricos, por lo que, si pueden usarse, se prefieren. El uso indiscriminado de muestras de distribución fuera de la normalidad conlleva el peligro de obtener conclusiones erróneas. 

En general, con pocos datos, es preferible, si no es difícil ni conlleva un alto coste de tiempo y dinero, realizar más determinaciones para poder aplicar pruebas paramétricas al lograr una distribución normal. El teorema del límite nos dice que si el tamaño de la muestra es suficiente, la distribución siempre tiende a ser normal, lo que juega a nuestro favor. También hay que tener presente que la mayoría de las veces no hay suficiente tiempo y dinero para realizar un número elevado de pruebas para calcular la variancia de la población (Ec. 1.1), por lo que se recurre a la variancia de la muestra (Ec. 1.2) 

σ² = (Σ(x_i-µ)²)/N      (Ec. 1.1) 
s² = [Σ(x_i-x­)²]/n-1   (Ec. 1.2) 

x_i: valor puntual o media de un conjunto pequeño de datos (muestra). 
µ: media de un conjunto infinito de datos (población) o valor aceptado como verdadero. 
x­: media de un conjunto finito de datos de la muestra. 

Es muy importante tener en cuenta que en las pruebas de significación estadística siempre se plantea la hipótesis nula "H₀" (no hay diferencias significativas entre los estadísticos de las muestras comparadas), y la hipótesis alternativa "H₁" (hay diferencias significativas). Se obtiene mucha mayor información cuando se puede rechazar la hipótesis nula, lo que quiere decir que los estadísticos de las muestras que se comparan son diferentes entre sí con una probabilidad mayor del 95%. Si no se puede rechazar la hipótesis nula (p > 0,05) se pierde mucha información porque no se puede decir que sean iguales, ni que sean diferentes porque la probabilidad es menor del 95%. 

Para analizar la dispersión se usa el concepto de "cuadrados medios (CM)". El cuadrado medio es la suma de los cuadrados de las diferencias de los valores individuales con respecto a un valor central (generalmente la media), partido por los grados de libertad que tiene esa muestra. Elevar al cuadrado cada diferencia tiene la ventaja de que hacemos positivas todas las diferencias, porque en realidad lo que queremos valorar es la distancia de los valores al valor central, sin importarnos si están por arriba o por debajo. El dividir por los grados de libertad, sencillamente nos permite comparar sumatorios de cuadrados "SC" entre grupos con distinto tamaño de muestra. Sería absurdo decir que una muestra con 50 valores tiene más dispersión que otra de 5 valores porque tiene un SC mayor, evidentemente la suma de 50 diferencias será mayor que la suma de 5, a no ser que las diferencias en la muestra con 5 valores sean muy grandes. Si recapitulamos un poco podemos imaginar la variancia como un cuadrado medio (Ec. 1.3) 

s² = [Σ(x_i-x­)²]/n-1 (Ec. 1.3) 

Brevemente se exponen en la tabla 1 métodos estadísticos que se pueden aplicar para comparar distintos tipos de variables. 

Para comprobar si la relación entre variables en una muestra es significativa, es decir, es poco probable que dicha relación se explique por fluctuaciones aleatorias del muestreo, se realizan las pruebas de significación estadística. 

II) Pruebas de significación 

II.A) Pruebas paramétricas 

1. Prueba t de Student 

Con esta prueba se pretende averiguar si dos muestras que tienen medias iguales, provienen de la misma población. 

Hipótesis nula "H₀" → µ₁ = µ₂; 
Hipótesis alternativa "H₁" → µ₁ ≠ µ₂ 

La prueba permite comparar la media con su valor verdadero o bien las medias de dos poblaciones. Se basa en los límites de confianza "LC" para el promedio x­ de n mediciones repetidas (Ec. 2.1). A partir de dicha ecuación tenemos: 

          µ= x­ ± t(s/√n) (Ec. 2.1) → x­ - µ = ± t s/√n (Ec. 2.2) 

s/√n: error estándar "EE" o desviación estándar "DE" de la distribución muestral de medias. Como las medias son √n veces más probables que los resultados aislados, la DE de las medias es √n veces menor que la DE de resultados aislados, siendo n el número de determinaciones con las que se calcula la media. 

t: "t de student" (tabla 2). Es un parámetro tabulado que depende de los grados de libertad de la muestra (n-1) "gl" y del intervalo de confianza que se quiera (generalmente 95%). 

 

Si x­ - µ obtenida en la muestra a comparar es menor que la calculada para un cierto nivel de probabilidad, no se rechaza la hipótesis nula de que x­ y µ sean iguales; es decir, sus diferencias son debidas a errores aleatorios y no existe un error sistemático significativo. 

Para comparar 2 medias experimentales el proceso es semejante. Se ha de tener en cuenta si los datos de las 2 muestras están apareados o no (figura 1): 

 

* Datos apareados: tienen la ventaja de permitir trabajar simplificando a una sola muestra (cuyos valores corresponden a la diferencia "D_i" entre cada par de datos apareados). Sustituimos x­ - µ (Ec. 2.2) por D­i - 0 porque el valor real de las diferencias, suponiendo que las dos muestras tienen la misma media, es 0. La DE se calcula con la muestra de diferencias. 

* Datos no apareados: como no se puede simplificar a una sola muestra, se ha de introducir el concepto de desviación estándar ponderada "sp" (Ec. 2.3). En la ecuación 2.2 se sustituye s por s_p y x­ - µ por x­₁ - x­₂ y el tamaño de muestra "n" se sustituye por N ponderado "(N₁ + N₂)/ N₁N₂". 

S_p=√[S(x₁ - x­₁)2+S(x₂ - x­₂)2+ ...]/(n₁+ n₂+ ... - N_s) (Ec. 2.3) 

n₁, n₂, ...: el tamaño de las muestras. 
N_s: número de muestras. 
(n₁+n₂+...-N_s): número de grados de libertad. 

Ejemplo 1: se analizaron dos sueros control (A y B) para la determinación de la glucemia. Se realizó sobre cada uno de ellos 5 determinaciones (tabla 3a) y se quiere determinar si estos dos sueros control son diferentes en relación al nivel de glucosa. 

Aunque el número de determinaciones es reducido podemos suponer que si realizáramos más determinaciones la distribución sería normal (teorema central del límite). Realizamos la prueba t de student de datos no apareados, ya que aunque las dos muestras tienen el mismo tamaño provienen del análisis de dos sueros supuestamente diferentes (tabla 3b): 

Como la diferencia de las medias es menor que 13.8, puede decirse que las dos muestras son significativamente iguales (p< 0.05). 


2. Pruebas de una y dos colas 

En las "pruebas bilaterales o de dos colas" se comparan dos muestras para saber si difieren entre sí, sin preguntarse cuál de ellas tiene mayor estadístico (Ej. media). Si se pretende evaluar qué muestra tiene el estadístico mayor (sesgo positivo) se realiza una "prueba unilateral o de una cola". Para un tamaño "n" determinado y un nivel de probabilidad concreto, los valores críticos de ambas pruebas difieren. Suponiendo una población simétrica, la probabilidad de la prueba unilateral es la mitad de la probabilidad de la prueba bilateral. Por ello, para encontrar el valor adecuado para una significación del 95% (p=0.05) en una prueba de una cola, se busca en la columna de p=0.1 de la tabla de pruebas bilaterales. 

La decisión de utilizar una prueba de una o dos colas, depende del grado de conocimiento del sesgo positivo o negativo que se tenga a priori. Nunca debe decidirse después de realizar el experimento, pues la decisión está influenciada por los resultados. 

Ejemplo 2: antes de analizar la vitamina A por cromatografía se realiza una extracción líquido-líquido. Si se quiere evaluar la recuperación de la vitamina A en el proceso de extracción, el sesgo será forzosamente negativo, pues nunca puede extraerse más de lo que hay. En este caso se aplicará una prueba de una cola. 

3. Comparación de variancias por contraste de Fisher 

Para comparar las variancias de dos muestras (S₁² y S₂²) se plantea la hipótesis nula y la alternativa. 

Hipótesis nula "H₀" → S₁² = S₂² 
Hipótesis alternativa "H₁" → S₁² ≠ S₂² 

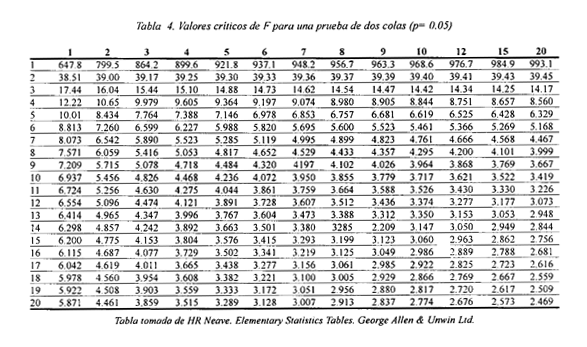
Dos muestras tienen variancias diferentes cuando la razón de sus variancias "F", colocando en el numerador la variancia mayor para que siempre sea mayor de uno, excede el valor crítico F tabulado. El valor crítico de F se escoge de la tabla 5 según los tamaños de muestra (n1, n2) y el nivel de significación deseado (generalmente 95%). Hay que tener en cuenta que aunque sólo se exponga la tabla de dos colas, se debe aplicar la tabla de valores F para pruebas de una o dos colas según el caso.
F=S1²/S2² (Ec. 2.4) → F ≤ F_tabulado (g l=n₁-1; n₂-1 y 95% significación) no se puede rechazar H₀ con una probabilidad de error menor del 5% (p < 0.05). 

4. Análisis de variancia (Anova) de un factor 

Está basada en la prueba de Cochran para estudiar la homogeneidad de las variancias de poblaciones origen de varias muestras. Si las muestras proceden de la misma población tendrán variancias semejantes, por lo que un análisis de variancias permitirá comparar sus medias. Es una prueba bilateral de comparación por contraste de Fisher de k medias, en la que se compara las variancias de las k medias (s²y­), con la variancia que debiera obtenerse si las k muestras procedieran de poblaciones con igual media [Sp²/n → siendo Sp la desviación estándar ponderada calculada entre las distintas muestras (Ec. 2.3)]. 

F= s²y­/ s²/n = CMMedias/CMResiduales (Ec. 2.5) 

El ANOVA de un factor se aplica para análisis donde, además del error aleatorio inevitable en las mediciones, hay un factor controlado (Ej. temperatura) o aleatorio (Ej. toma de muestra al azar). Hay que indicar que el ANOVA es una generalización de la "prueba t de student" (t y F son equivalentes al comparar sólo 2 grupos). 

Planteamos la hipótesis nula y alternativa: 

Ho:M₁=M₂=M₃= ... =M_k; H₁: M₁≠M₂≠M₃≠ ... ≠M_k 
(siendo M_k, la media k-ésima). 

Se define el tamaño de la población total como:

 N= n₁+n₂+n₃+ ...+n_k. 

Para una mejor comprensión pondremos un ejemplo para realizar el cálculo sencillo "con papel y lápiz": 

Ejemplo 3: se dan los resultados de cuatro análisis de purezas en % realizados sobre 5 muestras (tabla 5). Los datos se manejan respecto a una pureza basal de 98.5% para manejar números pequeños y simplificar los cálculos. Se pretende comparar si las medias son significativamente iguales:

F= CMMedias/CMResiduales= 0.195/0.133= 1.47. Se compara con el F crítico tabulado para una cola porque es de suponer que la variación intermuestra, si las muestras proceden de distinta población, sea mayor que la variación intramuestra. Si Fcalculado > Ftabulado →p ≤ 0.05 se puede rechazar H0 y admitir H1, osea que las muestras provienen de distinta población. 


5. Regresión y correlación 

Ambas técnicas permiten analizar la relación entre dos variables cuantitativas. Es muy común la confusión entre regresión y correlación a pesar de que son completamente distintas. 

5A) Correlación por ajuste de una recta con el criterio de mínimos cuadrados 

A partir de la matriz de datos con n pares de valores (x_i, y_i) se pueden representar los pares de valores por puntos en un diagrama de ejes cartesianos (figura 2). El eje de abscisas representa la variable X y el eje de ordenadas la variable Y. Los pares de valores (x_i, y_i) se representan por los puntos de intersección de las rectas que perpendicularmente a los ejes X e Y, pasan por los puntos x_i e y_i de dichos ejes. Para buscar la recta que mejor se ajusta al conjunto de puntos representados y evaluar el grado de ajuste a dicha recta, se determinan los coeficientes A y B de la recta de ajuste (Ec. 2.6) que hagan mínima la suma de los residuales "ei" al cuadrado (Ec. 2.7). 

y = A + Bx (Ec. 2.6) 

Los residuales "e_i" representan la distancia, perpendicular a la recta, de los puntos a la recta. 

Σe_i²= Σ1ⁿ [y_i-(A+Bx_i)]² (Ec. 2.7) 

Como las derivadas de una función al alcanzar los valores mínimos deben ser cero, los valores A y B se calculan (Ec. 2.8) haciendo cero las derivadas parciales del sumatorio de residuales (Ec. 2.7) con respecto a A y B, ordenada en el origen y pendiente¹ de la recta de correlación (figura 2): 

A= y­-B x­ , B = [Σx_iy_i - Σx_iΣy_i/n]/Σx_i²-(Σx_i)²/n (Ec. 2.8) 

¹Recordar que la pendiente es el valor de la tangente del ángulo que forma la recta con el eje de abscisas. 

Nota: es importante saber que la recta de correlación pasa por el punto (x­, y­) siendo x­, y­ las medias de los datos x_i e y_i. Aplicando la ecuación punto-pendiente de una recta podemos obtener la ecuación de la recta de mínimos cuadrados: 

y= y­ + B(x- x­) 

5.a.1. Descomposición de la suma de cuadrados 

Como se observa en la figura 2 para un sujeto "i" cualquiera, se verifica que: 

(y_i - y­)TOTAL= (^y_i - y­)_REGRESIÓN+(y_i-^y_i)_RESIDUAL (Ec. 2.9) 

y_i: valor aislado de y del sujeto i. 
y­: media del conjunto de valores y_i. Se supone el valor verdadero. 
^y_i: valor de y del sujeto i, calculado por la ecuación de la recta de mínimos cuadrados. 
Total: variación total, distancia desde y_i al valor medio de y. 
Regresión: variación explicada por la recta de regresión. 
Residual: variación no explicada. 

Y para el conjunto de los sujetos se demuestra que la variación total se descompone como: 

Σ(y_i - y­)²= Σ(^y_i - y­)²+Σ(y_i-^y_i)² (Ec. 2.10) 

5.a.2 Valoración del ajuste de la recta 

En el laboratorio es muy común el ajuste de datos experimentales a una recta, por ejemplo para construir la recta de calibración de una determinada técnica. El ajuste perfecto se da cuando la variancia residual es nula y todos los puntos están sobre la recta de regresión. El ajuste nulo se da cuando la variación explicada por la regresión es cero. 

Se define el coeficiente de correlación "r²" como la relación entre la variación explicada y la variación total. 

r² = SCRegresión/SCTotal = B² (SCx/SCy) (Ec. 2.11) 

El coeficiente toma valor de 1 cuando el ajuste es perfecto y 0 cuando es nulo. Es importante indicar que un ajuste nulo no quiere decir ausencia de relación, ya que sólo indica ausencia de relación lineal ( puede existir una relación de tipo parabólico, exponencial...). Hay que indicar que es preferible hablar de r² que de r porque r varía desde ­1 hasta +1, correspondiendo con una pendiente de la recta negativa o positiva, sin embargo r² siempre toma valores positivos. 

En algunas circunstancias se obtienen valores bajos de "r". Para valuar si el coeficiente es significativo se debe considerar el número de pares de valores usados en su cálculo. El método más simple es calcular un valor de t usando la ecuación 2.12. 

t= [|r|√(n-2)]/√(1-r²) (Ec. 2.12) 

El valor de t calculado se compara con el tabulado para el nivel de significación deseado, usando una prueba de t de dos colas con (n-2) gl. Si t calculado es mayor que el tabulado, H0 se rechaza (hay correlación significativa). H0: no existe correlación entre x e y. 

Hay que indicar que los cálculos anteriores permiten obtener la "recta de regresión de y sobre x" es decir, la recta que evalúa cómo varía y cuando x se ajusta a los valores elegidos. La "recta de regresión de x sobre y", la que supone que todos los errores ocurren en x , no coincide con la anterior salvo cuando r =1. 

5.a.3. Errores de la pendiente y ordenada en el origen de la recta de regresión 

Son errores importantes por lo que es muy útil evaluarlos. Para ello se define el estadístico sy/x a partir de los residuos de la tabla 8. 

s_y/x= √[Σ(y_i-^y_i)² / (n-2)] (Ec.2.13) 

Las DE de los parámetros A y B de la recta de mínimos cuadrados son: 

SB=s_y/x/√S(x_i-x­)² (Ec.2.14) 
SA=s_y/x√[Σx_i² /nΣ(x_i-x­)²] (Ec.2.15) 

SB y SA se pueden utilizar para estimar los límites de confianza de la pendiente y ordenada en el origen (B±ts_B/√n ; A±ts_A/ √n), donde t se obtiene para (n-2) gl. 

Una vez ajustada la recta de calibración, la señal de una muestra cualquiera y0 se extrapola para calcular la concentración x0. El cálculo del error en la estimación de x0 es complejo, pero podemos emplear la siguiente fórmula aproximada: 

S_x0=s_y/x/B√[1/m+1/n+[( y₀-y­)² /B²Σ(x_i-x­)2]] (Ec.2.16) 

m: nº de lecturas realizadas para calcular y0. 
n: nº de puntos de la recta de calibración. 

A partir de s se puede calcular los límites de confianza de x0. Hay que indicar que S_x0 es menor a medida que y₀ se aproxima a y­, de ahí la razón de elegir unas concentraciones para la recta de calibración que hagan que las muestras problema estén próximas a y­. El aumento excesivo de m y n genera mucho trabajo adicional y no disminuye apreciablemente S_x0 por lo que suele ser suficiente m=4 y n=6. 

5B) Regresión lineal 

La regresión lineal simple consta de dos etapas bien diferenciadas. En la primera etapa, meramente descriptiva, se utiliza el ajuste por mínimos cuadrados para hallar la ecuación de la recta que se ajuste mejor a los datos "recta de regresión". La segunda etapa, inferencial, estima la dependencia de la variable dependiente respecto a la independiente. 

5.b.1. Vertiente descriptiva o correlación 

Etapas: 

1. Cálculo de la recta de regresión por el ajuste de mínimos cuadrados (ver sección superior). 
2. Descomposición de la suma de cuadrados. 
3. Valoración de la bondad del ajuste por el coeficiente "r²". 

Hay dos índices estadísticos muy importantes: la covariancia y el coeficiente de correlación de Pearson. 

* Covariancia "S_xy": promedio de los productos de las desviaciones de las dos variables P_xy=(x_i-x­)(y_i- y­). Puesto que las desviaciones tienen signo, la covariancia será positiva cuando la nube de puntos en la representación y vs x tenga una forma lineal ascendente y negativa en el caso contrario. La unidad de medida de la covariancia es el producto de las unidades de medida de x e y. 

S_xy= Σ(x_i-x­)(y_i-y­)/n-1=SP_xy/n-1 (Ec. 2.17) 

S_xy: covariancia. 
SP_xy: sumatorio de los productos cruzados de las desviaciones de las dos variables → Σ(x_i-x­)(y_i-y­) 

* Coeficiente de correlación de Pearson "r_xy": se obtiene estandarizando la covariancia para eliminar la influencia de las unidades de medida, por lo que es una magnitud adimesional. Se define como: 

r_xy= S_xy/SxSy (Ec. 2.18) 

r_xy toma valores entre ­1 y +1. ­1: relación lineal perfecta negativa; +1: relación lineal perfecta positiva y 0: relación nula. Nota importante: el cuadrado del coeficiente de Pearson coincide con el cociente entre la variación explicada por la recta de regresión y la variación total (coeficiente de correlación, ecuación 2.11). 

5.b.2. Vertiente inferencial o regresión 

Como se ha dicho, la regresión lineal pretende deducir la relación lineal entre una variable dependiente, y otras independientes que la condicionan. El modelo exige que los datos de la población cumplan los supuestos de linealidad, homocedasticidad, independencia entre las observaciones y normalidad de las distribuciones condicionadas de la variable "y". Estos 4 supuestos se pueden resumir en que los términos de error o residuales para cada una de las distribuciones condicionales deben ser variables aleatorias independientes, distribuidas según la Ley Normal. 

* Linealidad: Las medias de "y" están sobre la recta: µ_i= α + ßx_i 
* Homocedasticidad: las variancias de la variable dependiente no se modifican con la variable independiente: 

σ²y(x1)= σ²y(x2)... = σ² 

* Ausencia de autocorrelación: un valor y_i no influye sobre otro valor y_j. 
Al igual que en el caso de la correlación, se estima el modelo de regresión mediante una recta: 

µ_i= α + ßx_i + ε_i (Ec. 2.19) 

ε_i: error residual. 

Estimación de los parámetros del modelo de regresión: se demuestra que los coeficientes A y B del ajuste de mínimos cuadrados son los mejores estimadores lineales de los parámetros a y b de la población. Así, α=A (ordenada en el origen de la recta de correlación, ecuación 2.7) y ß=B (pendiente de la recta, ecuación 2.8). 

En el trabajo de laboratorio muchas veces se necesitan técnicas que detecten errores sistemáticos en los resultados obtenidos con un método respecto a otro de referencia. Una posible relación entre dos métodos es una función lineal: 

Y= α + ßx + ε (Ec. 2.20) 

Donde α representa el error sistemático constante, ß el error sistemático proporcional y ε el error no sistemático (aleatorio) de los métodos. 

5C) Modelo de regresión ortogonal 

En el apartado anterior vimos que α y ß se estimaban por el ajuste de mínimos cuadrados suponiendo que X estaba desprovista de error. En este caso se debe considerar también el error de X, por lo que α y ß se estiman de forma que la suma de cuadrados de las distancias perpendiculares desde cada punto hasta la recta de regresión sea mínima: "modelo de regresión ortogonal". 

A₀= y­ ­ B₀ x­ (Ec. 2.21) 

B₀= (SC_y­SC_x)/2SP_xy+√{[(SC_y­SC_x)/2SP_xy]²+1} (Ec. 2.22) 

II. B) Pruebas no paramétricas 

Las pruebas paramétricas requieren que los datos sigan la distribución normal. Muchas veces nos interesa aplicar métodos que no requieran dicha hipótesis: 

* En muchos experimentos se utilizan muestras pequeñas de datos no pudiéndose aplicar el teorema central del límite. 

* Hay variables que, aunque se recojan numerosos datos, claramente no siguen una distribución normal. Así por ejemplo las concentraciones de anticuerpos en suero de una muestra de pacientes sigue una distribución log-normal. 

* Se emplean cuando interesa aplicar métodos más sencillos para una valoración inicial. Esta razón va perdiendo peso pues día a día son más numerosos los laboratorios que disponen de programas estadísticos de ordenador que simplifican enormemente la aplicación de tests paramétricos. 

1. PRUEBAS BASADAS EN TABLAS DE CONTINGENCIA. ESTUDIOS RETROSPECTIVOS CASO-CONTROL

El mejor diseño de un estudio es el diseño experimental, diseño aleatoriamente controlado de tipo prospectivo, en el que los individuos se asignan de forma aleatoria, bien al grupo de tratamiento o bien a un grupo control. Pero si el tratamiento conlleva un cierto peligro no se puede aplicar a humanos por razones éticas. En estos casos se realiza un estudio prospectivo de grupos "cohortes", se confrontan individuos expuestos con individuos análogos en todo lo que se pueda imaginar salvo en la exposición. Cuando la exposición se valora difícilmente o cuando la frecuencia de la enfermedad es muy pequeña resulta más práctico realizar un estudio retrospectivo por medio de tablas de contingencia, en el que se considera un grupo indiscriminado de individuos con enfermedad (casos) y sin ella (controles), y se observa la exposición a la que han estado sometidos. 

1.a. Prueba de chi-cuadrado de Karl-Pearson 

Consiste en un contraste de frecuencias o contajes observados (O) con los teóricos o esperados (E) representados en la tabla de contingencia de dimensiones 2x2 de la figura 3. Así, se define el parámetro chi cuadrado de la siguente forma: 

χ²= Σ(O-E)²/E (Ec. 2.23.a) 

Las frecuencias se ajustan a la distribución de Poisson, que tiene una propiedad poco habitual, la variancia coincide con la media. χ², por lo tanto, es una razón de tipo señal-ruido entre el cuadrado de la diferencia entre las frecuencias observada y esperada respecto a la media esperada. 

Nota importante: la prueba sólo se puede aplicar cuando el Nº total de observaciones es mayor de 50 y las frecuencias individuales esperadas no son menores de 5. 

Se compara el χ² calculado con el valor crítico tabulado (figura 3) en función del nivel de significación y del número de grados de libertad [gl de cada cada variable= Nº de clases ­1, siendo la clase cada una de las posibilidades en la variable; gl para la prueba es la multiplicación de los gl de cada variable. En el ejemplo de la figura 3 el número de gl=1]. Si el chi cuadrado calculado supera al tabulado, se puede rechazar H₀ y admitir H₁ (es decir, es poco verosímil (p< 0.05) que los resultados obtenidos sean debidos al azar). 

Nota: cuando hay sólo dos clases (un grado de libertad) o la frecuencia observada en una o varias clases es menor del 5%, se puede aplicar la "corrección de Yates" que implica sustituir cada O-E por |O-E |-0.5. 

Ejemplo 4. Se recogen los datos de peso y semanas de gestación de los niños nacidos en un hospital durante un año. Se tabulan en una tabla dos por dos, clasificándolos en 4 clases en función del bajo peso (0: peso >= 2500 g; 1: peso < 2500 g) y prematuridad (0 >= 36 semanas de gestación; 1: < 36). A partir de los datos recogidos "observados" calcular los datos esperados e indicar si la diferencia con respecto a los observados es debida al azar. 

Primero se comprueba que hay más de 50 observaciones y que las frecuencias observadas son mayores del 5%. Los valores esperados se calculan por medio de una simple regla de tres. Para el grupo de niños bajo peso "0", prematuros "0", el valor esperado se calcularía de la siguiente forma: 

Si en 411 recién nacidos (totales) hay 364 prematuros, en 387 recién nacidos con bajo peso habrá X recién nacidos prematuros. Aplicando una regla de tres se obtiene el valor esperado: 

X= 364*387/411=342.7. 

De igual forma se calcula el resto de valores esperados, que se indican en la figura 3. 

Cálculo de א² (tabla 10.a): 

Para 3 grados de libertad (4 clases ­1) א² crítico tabulado es 7.81. Como el valor de א² calculado es mayor que el valor crítico, se puede rechazar H0 con una probabilidad de error menor del 5%, por lo que significativamente hay diferencias que no son debidas al azar. 

1.b Prueba de chi-cuadrado de McNemar "א ²M" 

En el contraste de observaciones emparejadas se calcula א² de McNemar (ecuación 2.23.b) construyendo una tabla 2x2 diferente, en la que las celdas muestran las cuatro posibilidades de los pares caso-control: ambos estan expuestos, sólo los casos están expuestos, sólo los controles están expuestos, ninguno esta expuesto. Si no hubiera ninguna relación entre la enfermedad y la exposición sería de esperar que hubiera igual frecuencia cuando los casos están expuestos y los controles no, como en la situación contraria, por lo que el valor esperado en este caso es la media de los valores que no están en la diagonal principal. En el ejemplo 5 (tabla 10.c) el valor esperado sería E= b+c/2= 14. 

א²_M se calcula a partir de la ecuación 2.23.a considerando dicho valor esperado y aplicando la correción de Yates 

א²_M= [(b-c)-1]²/(b+c) (Ec. 2.23.b) 

Si א²_M es mayor que el tabulado 

Ejemplo 5: se realizó un estudio caso-control para estudiar el efecto potencial del consumo regular de tabaco sobre el carcinoma vesical. Para ello se contrastaron 50 pacientes con dicho cancer frente a 50 individuos control. En los casos había 35 que consumían más de 10 cigarrillos al día, así como 12 de los asociados a ellos en el grupo control. En los casos que no fumaban se asociaban 5 controles que fumaban. Calcular la א² de McNemar. 

La tabla 10.b sería la tabla clásica de contingencia, pero para el análisis de McNemar construimos la tabla 10.c. 

χ²_M= [(b-c)-1]₂/(b+c) = 17²/28= 10.32, valor mucho mayor que el tabulado para 1 gl (tabla 9) se rechaza H0 con una probabilidad de error menor del 5%, por lo que significativamente hay diferencias, no debidas al azar. 


1.c Prueba de chi-cuadrado de Mantel-Haenszel "χ²_M-H" 

χ² de Karl-Pearson equivale desde el punto de vista paramétrico a un t-test para dos categorías o un ANOVA para más de 2 categorías. χ² de McNemar equivale a un t-test de datos apareados. En el caso de un ANOVA de dos factores, un estadístico no paramétrico equivalente es χ² de Mantel-Haenszel. 

1.d Test exacto de Fisher 

Cuando las frecuencias observadas son menores del 5%, deben de aplicarse otros test alternativos a la prueba de chi cuadrado. Una posibilidad es valorar teóricamente la probabilidad de observar un valor tan extremo, o incluso más extremo que el observado realmente. A partir de la Ley binomial (Ec. 2.26 y 2.27), se puede demostrar que la probabilidad de que aparezca una configuración determinada en una tabla 2x2 (tabla 11) viene dada por la ecuación 2.24. 

p(k)= (a+b)! (c+d)! (a+c)!(b+d)!/N!a!b!c!d! (Ec. 2.24) 

K: es el menor número entre a, b, c, d. 

x!: factorial de x: x!=x(x-1)(x-2)(x-3) ... 1 

Se indica p(k) porque la probabilidad usada en el estadístico es toda la probabilidad de la cola, es decir desde k hasta el final de la distribución p(K→0) (ecuación 2.25). 

p(K→0)= p(k)+p(k-1)+p(k-2)+p(k-3)+ ... + p(0) (Ec. 2.25) 

Nota: para K- i (i=1, 2, ... k) se sustituye el valor de k en la tabla 2x2 por k-i y se suma +i en las celdas adyacentes para que las sumas parciales y totales de las celdas sean las mismas (ver ejemplo 6). 

Si p(k→0) supera 0.05 no se puede rechazar la hipótesis nula, que las diferencias son debidas al azar. 

Ejemplo 6: Se han tabulado, como indica la figura 4 los niños nacidos en un hospital durante un año en función de las semanas de gestación y aparición del síndrome de dificultad respiratoria "SDR". ¿hay diferencias significativas entre los niños prematuros y los no prematuros en cuanto al SDR?. 

De las cuatro clases el menor número de casos se da en recién nacidos no prematuros con SDR (prematuros=0, SDR=1), en la que sólo hay un caso (como en una clase hay menos de 5 % de casos no puede aplicarse la prueba de א²). Se calcula (Ec. 2.24) la probabilidad de tener de forma aleatoria 1 sólo caso o ninguno en esa clase (la probabilidad de la cola): 

p(1→0)= p(1) + p(0)= (404! 7! 364! 47!) / (411! 363! 41! 1! 6!) + (404! 7! 364! 47!) / (411! 364! 41! 0! 7!)= 1.05*10^-5 

Como la probabilidad de que las diferencias sean debidas al azar es mucho menor de 0.05, se puede afirmar que sí hay diferencias significativas. 

2. PRUEBA DE LOS SIGNOS 

A cada valor experimental se le resta la mediana postulada y se considera el signo de cada resultado, ignorando los resultados iguales a la mediana. Para contrastar si una preponderancia de signos, en uno de los dos sentidos, es significativa, utilizamos la Ley binomial. Esta ley establece que la probabilidad de que aparezcan r signos menos, entre n signos, viene dada por: 

P(r)=ⁿC_rp^rq^(n-r) (Ec. 2.26) 

ⁿC_r: nº de combinaciones de r elementos de un total de n elementos. 

ⁿC_r= n!/[r!(n-r)!] (Ec. 2.27) 

p: probabilidad de que aparezca un signo menos en un resultado. 

q: probabilidad de que en un resultado aparezca un signo más:

q^(n-r)=1-p^r. 

Si P(r) calculado es mayor que 0.05, no se puede rechazar H0, es decir, que los datos proceden de la mediana postulada. 

Ejemplo 7: un medicamento requiere que tenga una mediana del 5% en porcentaje del componente A. Analizando varios lotes del mismo se encontraron las siguientes concentraciones: 4.9, 4.8, 5.6, 6.1, 5.8, 6.2. ¿Cumple el medicamento la normativa con respecto al componente A?. 

1. Restando la mediana a cada resultado: -0.1, -0.2, 0.6, 1.1, 0.8, 1.2. Se observa que predominan las diferencias positivas. Para contrastar si el déficit de signos negativos es significativo utilizamos la ecuación 2.26. El número de combinaciones de 2 elementos negativos en un total de 6 elementos será, según la ecuación 2.27, ⁶C2 = 6!/2!4!=15. Por la definición de mediana es evidente que la mitad de valores están debajo de ella y la otra mitad encima, lo que indica que la probabilidad de tener un signo más, p, o menos ,q, en uno de los resultados es 1/2. Aplicando la ecuación 2.26 la probabilidad de que aparezcan 2 o menos signos negativos entre 6 signos es: 

P(≤2)=P(2)+P(1)+P(0)=15(1/2)²(1/2)⁴+6(1/2)¹(1/2)⁵+1(1/2)⁶ (1/2)⁰=22/64=0.344 

P(2): probabilidad de que aparezcan 2 signos negativos. 

P(1): probabilidad de que aparezca 1. 

P(0): probabilidad de que no aparezca ninguno. 

2. Para conocer si los datos difieren significativamente de la mediana realizamos una prueba de dos colas, en la que calculamos la probabilidad de obtener 2 o menos signos idénticos (ambos positivos o negativos) cuando se toman al azar 6 resultados que será el doble de P(≤2); 0.6875. 

3. Puesto que el valor experimental es mayor de 0.05, no se puede rechazar H₀, que los datos proceden de una población con mediana 5, con una probabilidad de error menor del 5%. 

La prueba de los signos puede utilizarse como una alternativa no paramétrica a la prueba t por parejas, y también para indicar si existe una tendencia en los valores con el tiempo (restando a valores iniciales, valores posteriores). 

3. PRUEBA DE RACHAS DE WALD-WOLFOWITZ

En otros casos nos interesa, además de evaluar el número de signos (+) ó (-), si éstos aparecen en una secuencia aleatoria o a rachas. Racha se puede definir como cada serie de valores con el mismo signo y tiene un significado semejante al significado popular de rachas, de buena o mala suerte. Una distribución aleatoria de signos debería tener un número de rachas determinado, porque si se acumulan mucho los signos positivos o negativos, quiere decir que ello no es debido al azar sino a que hay una tendencia no explicable por errores aleatorios. De igual modo, si el número de rachas es excesivo quiere decir que hay un continuo y regular cambio de signos positivos y negativos, tampoco explicable por el azar, sino por algún factor periódico que afecta a nuestras mediciones. 

Esta prueba, por lo tanto, evalúa si el número de rachas es demasiado pequeño o grande para aceptar H₀ (distribución aleatoria de los signos). Se tabulan para un nivel de significación determinado y un determinado número total de signos positivos y negativos, el número de rachas por debajo y por encima para las que se puede rechazar la hipótesis nula (tabla 12)

4. PRUEBAS BASADAS EN EL RECORRIDO DE LOS RESULTADOS 

En estas pruebas se usa el recorrido intercuartílico o recorrido total "w" de la muestra como medida de dispersión. 

Recorrido "w" se puede definir como la distancia entre el valor inferior y el superior de un conjunto de datos. Recorrido intercuartílico es la distancia entre el P25 y el P75*. 

* Un parámetro muy útil para situar puntos en la curva normal y en general en cualquier tipo de distribución, son los percentiles. El percentil de orden k representa el valor de la variable que deja por debajo el k% de los sujetos de la población. Así la mediana es la percentil 50 "P₅₀", que es medida de la tendencia central. Un tipo de percentiles muy usados son los cuartiles "Q₁=P₂₅, Q₂=P₅₀, Q₃=P₇₅", que indican, respectivamente, las posiciones en las que quedan por debajo el 25, 50 y 75% de los datos. 

Estas pruebas permiten, al igual que la prueba t de student, comparar la media de una población con un valor asumido como verdadero, o bien dos medias de dos muestras diferentes. Estas pruebas, simples pero afectadas por valores anómalos porque se sustituye la desviación estándar por el recorrido, se basan en el cálculo del parámetro T (ecuaciones 2.28 ó 2.29). 

T_i = |X­ - µ |/w (Ec. 2.28) 

µ: valor asumido verdadero. 

O bien, al comparar dos grupos de valores 1 y 2: 

T_d = 2|X­ ₁- X­ ₂|/(w₁+ w₂) (Ec. 2.29) 

Al igual que la prueba t de student, T_i o T_d calculado se compara con el valor tabulado (tabla 13) para n muestras y un nivel de significación de p=0.05. Si es más pequeño que el tabulado no se puede rechazar H₀. El TTABULADO permite calcular límites de confianza → X­ ±(T*W). 

5. VALORES ANÓMALOS "Q DE DIXON" 

Esta prueba, usada de forma abusiva, permite eliminar valores extremos. En general se recomienda no aplicarla, sugiriendo siempre mitigar valores anómalos con la recogida de más datos. Cuando la recogida de más datos no es posible y se cree realmente que el valor anómalo es consecuencia de un error sistemático sospechoso, se aplica con precaución. Esta prueba es una variante de prueba de recorrido en la que se calcula el parámetro "Q" 

Q= | X_sospechoso- X_{más próximo} | / W (Ec. 2.30) 

Si el valor Q calculado, para un determinado nivel de significación (generalmente p=0.05), supera el valor crítico tabulado (tabla 14), se rechaza el valor sospechoso. Una buena aproximación es que un resultado anómalo se puede rechazar si Q es mayor que √(2/n) (p=0.05) ó √(3/n) (p=0.01) siendo n el número de determinaciones, incluyendo el valor anómalo. 

6. PRUEBAS DE SIGNIFICACIÓN PARA DATOS ORDENADOS

6.a. Prueba de los signos de Wilcoxon 

Se aplica para muestras que se distribuyen de forma simétrica (mediana y media coinciden), pero no se desea suponer que siguen una distribución normal. La distribución simétrica permite desarrollar pruebas más potentes que el test de los signos. 

1) Se ordenan las diferencias con respecto a la mediana (o me dia) de mayor a menor valor absoluto, prescindiendo de los signos. 

2) Se jerarquizan asignándoles números que indiquen su orden, pero se mantienen sus signos. A los empates se les asignan posiciones promedio. 

3) Se suman los rangos positivos por un lado y los negativos por otro. El menor de estos dos sumatorios en valor absoluto, se toma como el estadístico de la prueba. 

4) Si el estadístico es menor que el valor tabulado (tabla 15) para un tamaño de muestra determinado y un nivel de significación elegido (generalmente 95%), se puede rechazar la hipótesis nula de que las dos muestras provienen de la misma población con una probabilidad de error menor del 5% (p < 0.05). 

Ejemplo 8: se encontró que los niveles de kaliemia para 7 niños eran de 4.1, 5.0, 4.5, 4.7, 5.1, 3.8. 4.0. ¿podrían proceder los datos de una población simétrica de mediana 4.5?. 

1. Las diferencias son -0.4, 0.5, 0, 0.2, 0.6, -0.7, -0.5. 

2. Se ordenan de mayor a menor valor absoluto: -0.7, 0.6, 0.5, -0.5, -0.4, 0.2, 0. 

3. Se jerarquizan manteniendo el signo: -1, 2, 3.5, -3.5, -5, 6. El cero no se incluye. 

4. La suma de los positivos es 11.5 y la de los negativos ­9.5. Se toma la menor de estas dos cifras como el estadístico de la prueba (-9.5). 

Como 9.5 es mayor que 2, el valor tabulado para una prueba de dos colas con n=7 y significación del 95% (tabla 15), no puede rechazarse H0, porque el error sería mayor del 95%. 

Esta prueba se puede usar como alternativa no paramétrica a la prueba t de datos apareados. El ensayo es muy sencillo. Se restan los valores por parejas y con las diferencias se realiza la prueba de los signos como se indica en los 4 pasos anteriores. Si el estadístico obtenido es menor que el tabulado, H₀ se puede rechazar con una probabilidad determinada. 

6.b Prueba de suma de rangos de Wilcoxon 

Es equivalente a la prueba U de Mann-Whitney. Se aplica para comparar dos muestras independientes que no pueden reducirse a un único conjunto de datos y por lo tanto no se puede aplicar la prueba anterior de los signos. Así por ejemplo, se utiliza para muestra, simétricas no normales y de distinto tamaño. 

1) Al igual que la prueba de los signos de Wilcoxon, los datos 
se ordenan y jerarquizan, con un número que indique su posición, de mayor a menor valor absoluto. Sin embargo se prescinde de los signos y los valores de una muestra se distinguen de la otra por una marca (Ej. subrayado). Si las mediciones de las dos muestras fueran indistinguibles, se esperaría que las posiciones subrayadas "1" y las no subrayadas "2" estuvieran mezcladas al azar en la lista. 

2) Se calcula el parámero T₁ y T₂ con las ecuaciones 2.31 y 2.32. 

T₁ = Σ₁-n₁(n₁+1)/2 (Ec. 2.31) 

T₂= Σ₂-n₂(n₂+1)/2 (Ec. 2.32) 

Σ₁: sumatorio de las posiciones subrayadas, Σ2: sumatorio de las posiciones no subrayadas 
n₁ y n₂: el tamaño de las dos muestras. 
n₁(n₁+1)/2 y n₂(n₂+1)/2: valores esperados para el sumatorio de posiciones de cada muestra. 


3) El menor de estos parámetros se compara con el valor tabulado para una prueba de una o dos colas, un nivel de significación determinado y tamaños de muestras n₁ y n₂ (tabla 16). 

Ejemplo 9. Sobre un suero se realizan 10 mediciones de creatinina, 6 por un método A y 4 por un método B. Los resultados se observan en la tabla 17, ordenados de menor a mayor, subrayados los del método A para distinguirlos de los del otro método. Se ha decidido aplicar la prueba de la suma de rangos de Wilcoxon. 

T₁=27.5-21=6.5
T₂=27.5-10=17.5

El menor de los T (T₁= 6.5), es mayor que 2, el valor crítico tabulado para tamaños de muestra n₁=6 y n₂=4, siendo una prueba de dos colas con una significación del 95%. H0 no puede ser rechazada porque la probabilidad de error sería mayor del 5% (p> 0.05). 

Nota: esta prueba se ve afectada cuando los valores promedios de las dos muestras son muy diferentes porque los valores de T1 y T2 serán parecidos, independientemente de la dispersión de ambas. Este problema se puede resolver estimando las medias de las dos muestras, y añadiendo el valor de su diferencia a cada valor de la muestra más pequeña, con lo que se consigue que ambas muestras tengan valores aproximadamente similares. 

6.c Test de la z para datos ordenados 

Si la muestra tiene más de 10 individuos, la estadística paramétrica renace de nuevo porque se puede utilizar el test de la z con buena aproximación. Sea N el tamaño total de la muestra y m el número de individuos del grupo con mayor parámetro T (ecuación 2.31 ó 2.32). El valor esperado de la suma de rangos es m(N+1)/2 y el valor de z calculado es [T+0.5-(m(N+1)/2)]/√(mn(N+1)/12)], valor que se compara con la tabla de valores z. 


6.d Prueba de Siegel y Tukey 

Es una variante de la prueba de suma de rangos de Wilcoxon. Esta prueba, que compara la dispersión de dos conjuntos de resultados, es una alternativa no paramétrica de la prueba F. 

1. Se disponen por orden creciente los datos de los dos grupos a comparar, subrayando uno de los conjuntos de resultados para diferenciarlo del otro. 

2. Se ordenan de forma que se asigna posiciones bajas a los resultados pequeños y altos y posiciones altas a los resultados centrales: a la medición más pequeña se le asigna la posición 1, a la más grande la posición 2, la medición inmediatamente inferior a la más grande se le asigna la posición 3 y a la posterior de la más pequeña la posición 4, la medición posterior a las dos más pequeñas se le asigna la posición 5 y así sucesivamente. Si el número total de mediciones es impar se ignora el valor central. 

3. Se calcula los parámetros T₁ y T₂ con las ecuaciones 2.31 y 2.32. 
Interpretación: si uno de los grupos tuviera una dispersión significativamente mayor que el otro, la suma de sus posiciones debería ser mucho menor, mientras que si las sumas de sus posiciones fueran similares los grupos tendría una dispersión parecida. 

4. El menor de estos estadísticos se usa para la prueba y se compara con el valor crítico tabulado, generalmente de una prueba de dos colas, a un p=0.05 (tabla 16). Si el estadístico es mayor que el valor tabulado, la hipótesis nula, es decir, que la dispersión de los dos grupos de datos es similar, debe ser aceptada. 

Ejemplo 10. Los resultados del ejemplo 9 se observan ordenados en la tabla 18, subrayados los del método A. Se ha decidido aplicar la prueba de Siegel y Tukey para evaluar si por los dos métodos se obtienen dispersiones diferentes. 

T₁= 36.5 ­ 21= 15.5 
T₂= 18.5 - 10 = 8.5 

El menor de los T (T₂= 8.5), es mayor que 2, el valor crítico tabulado para tamaños de muestra n₁=6 y n₂=4, siendo una prueba de dos colas con una significación del 95%. H0 no puede ser rechazada, los dos métodos no son significativamente diferentes (p> 0.05). 

6.e Prueba de Kruskal-Wallis 

Extensión del procedimiento de suma de rangos de Wilcoxon para comparar medianas de más de 2 muestras sin ningún tipo de emparejamiento. 

6.f Prueba de Friedman 

Se aplica con 3 o más conjuntos de resultados emparejados. Fue ideada por el famoso economista americano Friedman y utiliza de nuevo el estadístico X². Es similar en la práctica al método ANOVA aunque no tiene su capacidad. 

B.7. MEDIDAS DE RELACIÓN PARA DATOS ORDENADOS. PRUEBA DE CORRELACIÓN ORDINAL DE SPEARMAN

La prueba de correlación de Spearman es la más sencilla y empleada. Se calcula un coeficiente de correlación ordinal de Spearman "ρ", alternativa simple no parámetrica a la correlación lineal de Pearson. Se aplica cuando los datos están correlacionados linealmente pero no se distribuyen normalmente. 

Se calcula "ρ" (ecuación 2.33). 

ρ = 1 ­ [6 Σd_i²/(N³-N)] Ec. 2.33 

N: tamaño de la muestra. 
d_i: diferencia de rangos entre la dos medidas para el caso i 

Al igual que para el coeficiente de Pearson, el test de significación del coeficiente de Spearman se basa en un t-test (ecuación 2.34). 

t= ρ/√[(1-ρ²)/(N-2)] Ec. 2.34 

III) Interpretación de las pruebas de significación 

Hemos visto numerosos tipos de pruebas de significación, la mayoria de los cuales se incluyen en la tabla 19 que nos puede orientar en la prueba a aplicar según el tipo de variable dependiente e independiente. 

Nota: cuando las variables cuantitativas no cumplen la ley de distribución normal, se transforman las variables en cualitativas ordinales con varias categorías y se aplica el test no paramétrico correspondiente. 

La relación causa-efecto entre dos variables de una investigación no puede confirmarse sólo por la aplicación de una prueba de significación. Hay unas condiciones básicas que deben cumplirse para que una relación entre variables pueda ser interpretada en sentido causal: 

- Temporalidad: la causa debe preceder al efecto. 
- Asociación: obtener probabilidades significativas al aplicar pruebas estadísticas. 
- Ausencia de espuriedad: que no haya una 3ª variable causa de ambas. 

Es imprescindible para medir la relación causal entre las variables investigadas, que el diseño de la investigación sea el correcto. Aplicar un test de significación es sencillo y con ligeros conocimientos en estadística también es fácil elegir el correcto entre la batería de los disponibles, que no son todos los que en este resumen se han descrito. Hay otros problemas en estadística mucho más importantes que no se consideran, por desconocimiento o por dificultad pero que marcan de forma irreversible la calidad de toda la investigación y la fiabilidad de los datos y conclusiones logradas. 

Multitud de laboratorios toman muestras de una población (paciente) sin valorar si son representativas, gastan enormes recursos en su análisis y los resultados obtenidos se creen asociados al paciente, cuando en realidad, casi siempre, están asociados solamente a esa muestra. Y lo que es peor, se toman decisiones clínicas sobre la base de resultados obtenidos de una sola muestra, con un solo análisis de la misma, eso sin tener en cuenta los errores sistemáticos graves que se pueden cometer por mala calibración y control del método analítico, ni los errores por confusión entre muestras y/o informes que se cometen al tratar conjuntamente tantas muestras, como se tratan en los laboratorios de análisis clínico. 

En investigación los errores graves cometidos sobre muestras individuales se mitigan, pero aparecen muchos defectos que invalidan los resultados obtenidos: 

* Población a estudiar no idónea y/o sesgada. 
* Existencia de sesgos en la muestra escogida de la población a estudiar (muestra no representativa). 
* Obviar que las diferencias entre los grupos escogidos pueden ser debidas a errores sistemáticos y/o aleatorios. Querer ver diferencias demasiado pequeñas como apreciables. 
* Mala elección del grupo control de comparación, o elección sesgada del mismo. 
* Nulo control en las variables que modifican los resultados obtenidos (tiempo de toma de la muestra, origen y condiciones de conservación y procesamiento de la misma, ...). 
* Falta de diseño previo en la investigación o diseño erróneo. 
* Tratamiento subjetivo de los resultados obtenidos (descarte de datos anómalos o que no interesan, falsedad en el tamaño de la muestra analizada, falta de comprobación de la normalidad de la muestra, aplicación de tests inapropiados por interés, ...). 

El control de calidad y diseño de investigación pueden ser temas para otro trabajo, ahora sólo indicar de forma esquemática los pasos a seguir en la investigación de la población (Figura.5). 

---

NOTA: Algunos caracteres especiales o símbolos matemáticos no se pueden representar en html, por lo que las fórmulas pueden no corresponder exactamente con la versión impresa. Se recomienda consultar este artículo en la versión en papel de la Revista de Diagnóstico Biológico

---

 

Bibliografía 

* Gary DC. Analytical chemistry, Fifth edition. Capítulo 2: data handling, páginas 14-64. John-Wiley & sons, Inc. 1994.          [ Links ]

* Kellner R, Mermet JM, Otto M, Widmer MM. The Approved Text to the FECS Curriculum Analytical Chemistry. Capítulo 2: the analytical process, páginas 25-40 y capítulo 3: Quality assurance and quality control, páginas 41-67. Wiley VCH editors, 1998.          [ Links ]

* McCormick D, Roach A. Analytical chemistry by open learning ACOL. Measurement, statistics and computation. John Wiley & Sons, 1987.          [ Links ]

* Miller JC, Miller JN. Estadística para Química Analítica. segunda edición. Addison-Wesley Iberoamericana, 1993.          [ Links ]

* Neave HR. Elementary Statistics Tables. George Allen & Unwin Ltd.          [ Links ]

* Norman GR y Streiner DL. Bioestadística. Mosby/Doyma Libros, SA. 1996.          [ Links ]

* Skoog DA, West DM and Holler FJ. Fundamentals of Analytical Chemistry, Fifth edition. Capítulo 2: evaluation of analytical data, páginas 6-56. Saunders College Publishin, 1998.        [ Links ]

* Varcárcel M. Principios de química Analítica. Capítulo 2: propiedades analíticas, páginas 51-121. Springer-Verlag Ibérica 1999.         [ Links ]