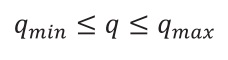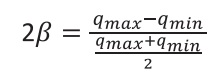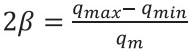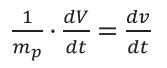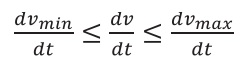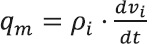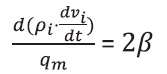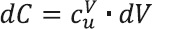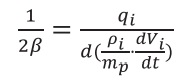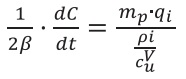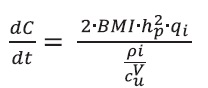INTRODUCTION
Nutrition therapy is a complex area of the healthcare system that encompasses the patient and clinical context, medical decision making, pharmacological aspects, supply issues, and costs, thus composing a complex system. Integration of these domains occurs individually in nutritional plans in an heuristic and iterative way, taking into account patient and formula characteristics with a limited capacity for the provider to make in-scale calculations to include pharmaco-economical aspects.
Although sufficient for bedside decision making, this method does not provide a comprehensive and integral view of critical domains in nutrition therapy. From a practical standpoint, the formulation in a simple model of these areas and its relationships as a general mathematical formula could provide the necessary equivalence to study dependence and consequence between equation terms.
The objective of this theoretical study is to provide a simple mathematical model that describes critical aspects of nutrition therapy.
CLINICAL NUTRITION AS A SYSTEM
Overview
Healthcare systems are often (or should we say always?) interpreted as hospitals or even healthcare services. However, when considered a system, healthcare systems attract to themselves a whole epistemological approach for analyzing several of their issues. In order to proceed with a real systemic analysis of healthcare systems, one must be able to describe its boundaries, structure, purpose and functioning.
Systems boundaries are important definition elements of systems, since they are responsible for distinguishing a system from another system or its environment as barriers or fences. Through its boundaries, one is able to clearly express what the system is and what the system is not. It is obvious, but not unnecessary, to say that different boundary definitions will impact the comprehension of the system described. On the other hand, it is kind of a desirable advantage of the approach, since different points of view can be used to understand the whole and complete each other.
A literature review should be carried out for the sake of describing the communis opinio of scholars around the globe. Nonetheless, we shall progress with the definition of the boundary of our healthcare system by using the firm as the interaction unit to describe.
The counterpart of a system's boundary is the system's environment. While the boundaries limit the system as part of the universe being studied, the environment is the remainder outside the boundaries. The environment can be divided into the microenvironment, which directly impacts the system, and the macroenvironment, which indirectly impacts the system.
Patient subsystem
The most important subsystem of a healthcare system is the patient. Health and patients are seen as the end of all the efforts of healthcare. The key characteristics of a patient subsystem for a clinical nutrition system are anthropometric measures, intensity of disease, type of disease, and comorbidities.
Pharmacological subsystem
Since nutrients must be supplied to patients in healthcare systems, especially when subjected to enteral and parenteral nutrition therapy, pharmacological subsystems play an important role in providing adequate solutions with enough concentrations. The technological capabilities to provide such solutions are limitations for the whole healthcare system, e.g., scarcity of industrialized enteral formulas with energy-to-nitrogen ratio < 1:60 or very low carbohydrate content (< 20 grams per liter).
Financial subsystem
Any flow in a modern organization falls subject to financial consideration. Nutrient flow and nutrition therapy inputs are no exception to this rule. However, in a clinical nutrition system the financial subsystem may be expressed by the resulting cash flow of the operation and the unit cost achieved by the deal between the demanding healthcare system and the pharmacological supplier.
Medical subsystem
Finally, the medical subsystem is responsible for therapy best practices and policies, such as target intake definition and the minimum precision admissible for the resulting integration of all the previous subsystems. Examples are clinical guidelines for daily macronutrient content, e.g., caloric intake between 25 and 30 kcal·kg-1·d-1
METHODS AND RESULTS
In this theoretical study, linear equations and simple calculus techniques were used to determine the coupling equations of the clinical nutrition system.
For prescription of industrialized formulas (IF) we applied an acceptable range described in society guidelines (1). In the case of caloric needs, the recommendation lies between 25 and 30 kcal·kg-1·d-1. These statements usually are expressed as a precise value or as an interval:
The guidelines can be rewritten as ratios. Rewritten as a ratio, has the form:
whereas q = goal normalized by patient's mass, mn = total nutrient/caloric intake, mp = patient mass, t = time interval
The nutritional goal per patient can be stated as a point inside the interval of recommendation and rewritten as an inequality:
The interval represents possible choices of prescription for a given nutrient. Inside this interval, the prescriptor arbitrates an amount of nutrients or calories per time period. This band of tolerance determines the length of the interval between two limit values accepted by the prescriber where the goal may be found, e.g., 25 to 30 kcal·kg-1·d-1 in terms of calories, or 1.2 to 1.5 g ptn·kg-1·d-1 in terms of protein. The narrower the band, the more precise the prescription will be. For example, an interval between 25 and 27 kcal·kg-1·d-1 has a narrower band of tolerance than the interval between 25 and 35 kcal·kg-1·d-1.
In clinical practice, using formulas with a defined composition implies sacrificing the precise meeting of the goal of a nutrient to meet another one, more relevant at the time. For example, in order to attain a goal of 1.5 kcal·kg-1·d-1 and 22 kcal·kg-1·d-1 with one of two available formulas may impose a choice in favor of the one that attends the protein goal even if it does not attend the precise caloric goal. If clinical requirements mandate a more precise interval, the prescriptor turns the band narrower, e.g., caloric target between 27.5 and 29 kcal·kg-1·d-1.
This band of tolerance may be represented as an adimensional variable, obtained by two times the distance between qm and qmax or qmin, as follows.
Whereas the numerator represents the interval between upper and lower nutritional limits of tolerance (qmax - qmin), and the denominator is the arithmetic mean that represents the middle of the interval, i.e., the precise nutritional target, qm.
The volume of the nutritional formula in the prescription will be viable when in a minimum amount to satisfy n restrictions posed in nutritional planning, since there is an specific density for each nutrient in the compound. This postulate was presented elsewhere (2). The volume per unit of time can be calculated by dividing:
Where qm is the target or recommended intake of the ith component of a nutritional strategy, mp is the patient mass, pi is the density of the ith component in a formula. For example: 25 kcal·kg-1·d-1 x 60 kg / 1.0 kcal/mL = 1500 mL·d-1.
Following Eq. (2), there is a band of tolerance for volumes per day, a measure of flow rate.
Let V be the volume flow rate per patient mass per unit of time. We can divide 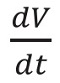 by the patient mass altering the patient mass dependence, without loss of generality.
by the patient mass altering the patient mass dependence, without loss of generality.
For example, if a target is achieved with 1500 mL·d-1, dividing by a patient mass of 60 kg would result in 25 mL·kg-1·d-1.
In this way, we can rewrite equation 6 as follows:
Since the nutrient mass to be administered is dependent on formula volume, let rewrite the equation (5) for:
In other words, the nutrient mass offered is dependent of flow per unit mass of patient multiplied by nutrient density of the formula. Let Vi be the lower limit accepted of flow rate interval for a given nutrient or calorie.
The equation (4) can be rewritten in terms of volume v of industrialized formula.
Now, let us consider the following relation that describes cost relations:
where dC = incremental costs related to using a volume of a nutritional formula (dV) with an unitary cost per volume (Cvu).
Equation 11 can be rewritten into by multiplying by -1
Now multiplying both by  , the cost relation, we obtain a descriptive equation of a whole system involves in nutrition therapy:
, the cost relation, we obtain a descriptive equation of a whole system involves in nutrition therapy:
Equation 14 can be rewritten representing mp as a function of body mass index (BMI) and patient height in meters. Replacing Eq (15) in the left side numerator, followed by simple algebraic replacement, we have:
DISCUSSION
As far as we know, we provided the first mathematical description of a nutrition therapy model that encompasses four critical aspects: patient attributes, expert decision making, nutritional formula characteristics, and costs. These critical elements are present in nutrition therapy planning whether enteral, parenteral or oral supplements. A mathematical representation has special properties that provide both a formal and quantitative study of the area, revealing unsuspected and quantitative relations among variables. This can open areas of investigation for future studies and multidisciplinary research.
Presented as equality, the isolation of an aspect from the left side can be represented as a combination of other terms. In this way, it is possible to study each of the variables as a function of the others and identify relationships between them. Another important consequence is the fact that the equation reveals multiplicative, not additive, properties that result from the relationships between the variables. The immediate consequence is that small changes in variables such as patient height, formula nutritional density, or cost per milliliter can significantly change cash flow. This can be illustrative of the potential for second-order effects, hitherto unquantified.
We can observe for example that cash flow is proportional to BMI until a limit of 29, because at 30, guidelines suggest lower caloric targets. Mean stature impacts the cash flow in a quadratic relation, and this can be relevant for national or regional means. Hypothesis as “Is cash flow higher in countries with higher height means than in countries where the mean height of the population is low?”. The equation also lends itself to comparing and identifying among different formulas and modalities (such as parenteral nutrition and mixed strategies as supplemental parenteral nutrition) that meet patient needs, the one that offers the most adequate cash flow for the economic scenario in question.
Formula density is inversely proportional to cash flow, and if other restrictions are satisfied, the selection of a higher density formula may be useful for reducing the amount of volume prescribed and overall costs. The use of nutritional formulas is not dissociated from the use of infusion pump circuits and their associated operating costs, so this issue may be relevant depending on the economic context.
Medical decision making is an unsuspected element in cash flow. At the bedside, nutritional planning is based on clinical judgment and takes into account guidelines. Common nutritional guidelines provide a wide margin of prescription, i.e., as seen in the relative distance between 25 and 30 kcal·kg-1·d-1 — greater than 20 %. A goal for calories or nutrients such as proteins, carbohydrates or lipids (usually less common) is set by the multidisciplinary team. Often, in the nutritional plan composed of independent target points, precision is sacrificed to optimize strategic nutrients for each clinical moment, which can result in higher cash flow as a second-order effect.
We call t this tolerability range around an optimal setpoint for each of the nutrients that is called a beta. The greater the tolerance range, or beta, the greater the tolerance for departing from the intention of the initial prescription: e.g., a band of caloric tolerance between 25 and 30 kcal·kg-1·d-1 denotes a lower precision than a band of caloric tolerance between 27,5 and 30 kcal·kg-1·d-1. It is still important to mention that beta is, among all elements of medical decision making, the one that is intrinsically linked to clinical reasoning, since clinical judgement implies clinical examination, laboratory panels and other sources of information, all of that integrated in the act of decision making or as beta definition. The freedom to expand, narrow or change the range according to patient needs is exclusive to the prescriber. On the other hand, when studying beta as an isolated term in the equation we can hypothesize that it may be restricted by other variables, such as cost per volume unit, available formula density, and patient mass.
The impact of this tolerability on cost is often not systematically considered in specialized practice at the bedside, possibly due to the limited computational capacity to take into account so many variables and also due to the lack of quantitative models. We argue that the determination of beta is a marker of the heuristic process in decision making and this field of research deserves further study.
In terms of bedside perception of bedside prescription, what is offered for the patient is a flow of homogenous nutritional formula that is administred, and cash flow is directly related to the delivery of a fixed proportion of nutrients per volume unit. The higher the flow of nutrients or calories, the higher will be the cash flow. In the actual scenario, with individualized importance of some nutrients as proteins, branched chain amino-acids, or carbohydrate restriction, it will be necessary to partition this term in each individualized nutrient species with its specific delivery. A perfectly adequate formula for the patient would be, at least in theory, cheaper than the formulation of formulas that meet the individualized compliances of each of the nutrients (macro and micro).
The model may shed light on cost per volume (CPV) as a strategic and organizational element. In models where payment for the service is the rule, the CPV will be considered as ideal as its minimization, safeguarding the care of the patient needs. In different models of healthcare financing, e.g., Brazil, CPV may be as optimal as maximizing cost. Taking into account these characteristics, this can be a critical factor for determination of a formula portfolio.
Our model has limitations and further developments must partition subcomponents in each term and use of mixed strategies of nutrition therapy, as supplementary parenteral nutrition. The model does directly not take in account operational aspects that interfere in nutritional formula delivery and other human factors. As far as we know, the model is the first approach for establishing quantitative, mathematical relationships between the factors involved in the prescription of nutritional therapy and, more specifically, with cash flow. Although it provides cash flow information as a function of other related variables, it does not intend to have predictive power, given the natural variations in the patients' clinical course, as well as any clinical needs or complications that require the replacement of the formula or nutritional strategy.
Unit cost is another critical determinant of cash flow. In our model, unit cost encompasses a wide array of factors that may influence the final cost per unit of volume. This factor is derived from several other technical and organizational aspects such as raw material costs, pharmacotechnical elements, logistical aspects of distribution, and other operational costs related to administration such as infusion devices, taxation, exchange rates for importation, contribution margin, and private business strategy. Externalities such as economic crisis, cambial rates, pandemic issues may be taken in account as relevant factors in these dynamics. Further development of the model will provide a description of quantitative relations among those factors, the relevance in each one of them according to the specific scenario and its impact in the final cost.
The notion that nutritional therapy makes up an intricate system of relationships with other domains directly or indirectly related to care was intuitive. The contribution of this formula lies in describing in a quantitative and simplified way the relationships between these different aspects. In a scenario of limited resources, where the use of technology must be judicious, tools like this can serve as support for medical training, especially with regard to care and rigor in decision making, the study of the impact of macro and microeconomic elements, and the development of new formula composition solutions.
Although other variables could have been included in our model, the mathematical formula presented here states for the first time quantitative relations among these areas, and may have a status of a general law for cash flow in nutrition therapy.
CONCLUSION
The assumptions are that the nutrition therapy environment can be described by four quantitative domains as patient characteristics, medical decision making, pharmacological aspects, supply issues, and costs. A mathematical model can correlate these dimensions and has a status of general law, since it can be used not only in nutrition therapy and enteral or parenteral nutrition scenarios but in any area of nutrition science.