Mi SciELO
Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO  Similares en Google
Similares en Google
Compartir
Gaceta Sanitaria
versión impresa ISSN 0213-9111
Gac Sanit vol.16 no.3 Barcelona may. 2002
Algunos aspectos metodológicos sobre los modelos edad-período-cohorte. Aplicación a las tendencias de mortalidad por cáncer
J.R. Gonzáleza / F.J. Llorcab / V. Morenoc
aServicio de Prevención y Control del Cáncer. Institut Català d'Oncologia.
bDepartamento de Medicina Preventiva y Salud Pública. Facultad de Medicina de la Universidad de Cantabria.
cServicio de Epidemiología y Registro del Cáncer. Institut Català d'Oncologia.
Correspondencia: Dr. V. Moreno.
Servei d'Epidemiologia i Registre del Càncer. Institut Català d'Oncologia. Avda. Gran Via, s/n. km 2,7. 08907 L'Hospitalet de Llobregat. Barcelona.
Correo electrónico: v.moreno@ico.scs.es
Recibido: 28 de diciembre de 2001.
Aceptado: 20 de febrero de 2002.
(Some methodological aspects of age-period-cohort models. Application to cancer mortality trends)
Resumen
Los modelos edad-período-cohorte suelen utilizarse en estudios de epidemiología descriptiva para analizar las tendencias de la incidencia y de la mortalidad para valorar el efecto temporal de la ocurrencia de un evento. La relación lineal exacta existente entre estos tres efectos hace que los parámetros del modelo completo no puedan estimarse, lo que se denomina no identificabilidad. En estas notas se explicarán dos de los métodos más usados para analizar modelos edad-período-cohorte: uno se basa en funciones de penalización y otro en funciones estimables (tendencia lineal y curvaturas o desviaciones). Ambos métodos se ilustrarán con dos ejemplos en el que se analizan la tendencia temporal de la mortalidad por cáncer de pulmón y mama en las mujeres de Cataluña. Estos ejemplos ilustran que los métodos basados en funciones de penalización tienden a atribuir la tendencia a un efecto cohorte exclusivo, por lo que se aconseja utilizar los métodos basados en funciones estimables.
Palabras clave: Tendencias temporales. Modelos edad-período-cohorte. Epidemiología descriptiva. Mortalidad por cáncer.
Abstract
Age-period-cohort models are usually used in descriptive epidemiological studies to analyze time trends in incidence or mortality. The exact linear relationship between the three effects of these models has the effect of making the parameters of the full model impossible to estimate, which is called non-identifiability. In these notes two of the most frequently used methods to analyze age-period-cohort models will be explained. One is based on penalty functions and the other on estimable functions (drift and curvatures or deviation from linearity). Both methods will be illustrated with two examples in wich temporal trends of breast and lung cancer mortality in women from Catalonia in Spain will be studied. These examples show how the methods based on penalty functions tend to attribute the trend exclusively to a cohort effect. Consequently, the use of methods based on estimate functions is recommended.
Key words: Time trends. Age-period-cohort models. Descriptive epidemiology. Cancer mortality.
Introducción
Los modelos edad-período-cohorte suelen utilizarse en estudios de epidemiología descriptiva para analizar las tendencias de la incidencia y la mortalidad por diferentes enfermedades como cáncer1-3, suicidios4 o sida5. También se ha aplicado en estudios sociológicos6 y, en general, pueden aplicarse a cualquier situación en la que se pretenda valorar el efecto temporal de la ocurrencia de un evento.
Una de las motivaciones principales de analizar los modelos edad-período-cohorte es estimar el efecto de cada uno de estos factores por separado en la evolución de las tasas. El efecto de la edad representa el cambio en las tasas asociado a la edad. Este efecto siempre es importante, pues la aparición de enfermedades crónicas suele aumentar al aumentar la edad. Los efectos período y cohorte, conjuntamente, responden a cambios en las tasas asociados al tiempo. El efecto período representa cambios en las tasas debidos a factores localizados en un momento del tiempo y que influyen a todos los grupos de edad simultáneamente. El efecto cohorte se asocia a factores que afectan a una generación y provoca cambios en las tasas de magnitud diferente en sucesivos grupos de edad, en sucesivos períodos. Un ejemplo de efecto período puede ser la introducción de un nuevo tratamiento que reduzca la mortalidad en todas las edades, la exposición a un agente que afecte a la población en su totalidad o el cambio en los procesos de diagnóstico como, por ejemplo, la introducción del antígeno prostático específico (PSA) en la detección precoz del cáncer de próstata7. Los ejemplos de efecto cohorte suelen estar asociados con hábitos o exposiciones de larga duración, como el consumo del tabaco, de manera que diferentes generaciones están expuestas a diferente nivel de riesgo. En consecuencia, suele interesar identificar si los cambios temporales de las tasas están asociados al período de diagnóstico o a la cohorte de nacimiento, objeto que no siempre es posible. En esta nota metodológica explicaremos las técnicas estadísticas más empleadas para tratar de identificar cuál de los efectos temporales es más importante.
El problema de no identificabilidad
Generalmente se dispone de información sobre los casos observados de una enfermedad resumidos en una tabla de dos entradas: el grupo de edad y el período calendario en que se registró el evento de interés (diagnóstico si se trata de incidencia o defunción si es mortalidad). Con esta información, se pueden calcular fácilmente las cohortes de nacimiento (fig. 1) según la fórmula:

| Figura 1. Cálculo de las cohortes de nacimiento a partir del período y de la edad de diagnóstico |
 |
donde al grupo de edad i con evento en el período j le corresponde la cohorte de nacimiento k. En la fórmula, E es el número total de grupos de edad y P el número de períodos. El número de cohortes diferentes es E + P 1.
Una vez que hemos identificado los componentes de los modelos edad-período-cohorte, podemos analizarlos como un modelo lineal generalizado. El modelo asume que el número de casos en cada grupo de edad i, período j y cohorte k sigue una distribución de Poisson de media qijk, donde i = 1,..., E; j = 1,..., P y k = 1,..., E + P 1. En este modelo los 3 efectos (edad, período y cohorte) actúan de manera multiplicativa sobre la tasa,  donde Nijk es el número de personas-año en el grupo de edad i, período j y cohorte k. De esta forma, el logaritmo del valor esperado de la tasa se puede escribir como una función lineal del efecto de la edad, el período y la cohorte mediante la fórmula:
donde Nijk es el número de personas-año en el grupo de edad i, período j y cohorte k. De esta forma, el logaritmo del valor esperado de la tasa se puede escribir como una función lineal del efecto de la edad, el período y la cohorte mediante la fórmula:

donde µ representa el efecto promedio, ai representa el efecto del grupo de edad i, bj el efecto del período j y gk el efecto de la cohorte k.
La fórmula para la construcción de las cohortes de nacimiento (fig. 1) muestra que existe una dependencia lineal exacta entre los tres factores. Por ello, para estimar los parámetros de (2) debe decidirse una serie de restricciones adicionales8-10. Debemos notar que los grupos de edad y período de diagnóstico deben de ser del mismo tamaño (generalmente 5 años), puesto que grupos de distinto tamaño hacen que el cálculo de las cohortes por esta fórmula asigne a una misma cohorte individuos pertenecientes a un grupo de años de nacimiento diferentes.
Las restricciones que se suelen introducir para cada efecto, son del tipo a1 = 0, b1 = 0 y g1 = 0 o a1 = aE , b1 = bP , g1 = gE+P1. Como en la regresión de Poisson el exponencial de cada parámetro se interpreta como una razón de tasas, una restricción del tipo ai = 0, bj = 0 y gk = 0 equivale simplemente a establecer cuáles son los grupos de edad, período y cohorte que se utilizan de referencia (razón de tasas = 1). Pero aún falta eliminar otro parámetro, hecho que da lugar a lo que se conoce como problema de no identificabilidad del modelo. En la práctica esto significa que se pueden obtener infinitos modelos máximo-verosímiles con diferentes parámetros (es decir, diferentes estimaciones de los efectos de edad, período y cohorte), pero que, sin embargo, producirán la misma predicción para cualquier combinación de edad i, período j y cohorte k. De esta forma, si la única finalidad del análisis es realizar predicciones sobre las tasas, entonces cualquiera de los modelos de tres factores es igualmente adecuado. Holford muestra cómo diferentes estimaciones pueden hacer rotar hasta 180° la pendiente del efecto período mientras los efectos de cohorte y de edad rotan en el sentido contrario9. Este hecho es debido a que la relación lineal descrita en (1) permite que podamos modificar los parámetros según estas ecuaciones:

así se obtienen infinitas soluciones con el mismo ajuste modificando arbitrariamente el valor de l, que se conoce como el parámetro de no identificabilidad. Podemos obtener la restricción extra que nos falta para identificar los parámetros, proponiendo algún método para obtener l que confiera a la solución una propiedad deseable.
No obstante, antes de emplear los métodos para determinar l, es recomendable representar gráficamente los efectos crudos y analizar si los modelos simplificados (edad-período o edad-cohorte) son suficientes para explicar los datos9. En este primer paso se puede realizar un test de la razón de verosimilitudes para comparar cada modelo de dos factores con el modelo de tres factores. Si de esta comparación se deduce que alguno de los modelos de dos factores no es peor que el de tres, entonces elegiremos el modelo dos factores y no se planteará el problema de no indentificabilidad. Otra posibilidad es calcular el criterio de información de Akaike (AIC), que permite comparar el ajuste de una serie de modelos relacionados teniendo en cuenta el número de parámetros que emplean. El AIC se calcula como 2 veces el valor del logaritmo de la función de verosimilitud (deviance) más dos veces el número de parámetros (p) del modelo (AIC = deviance + 2p). El modelo con menor AIC es el que mejor ajusta con relación al número de parámetro que emplea. En la mayoría de situaciones, estos análisis no suelen ser concluyentes para decidir si la tendencia temporal observada es debida a un efecto período o cohorte, ya que generalmente el modelo de tres factores es el que suele ajustar mejor. Debe tenerse en cuenta que aceptar un modelo de dos factores equivale a considerar que el tercer factor no tiene ningún efecto (es decir, que todos sus coeficientes serán iguales a cero), lo que en el fondo es una forma más de elegir arbitrariamente el parámetro de no identificabilidad l.
Funciones de penalización
Osmond y Gardner12 sugieren que la restricción extra que necesitamos se puede conseguir minimizando una función de penalización. Esta función mide la distancia, en el espacio de parámetros, entre los tres modelos de dos factores (edad-período, edad-cohorte, período-cohorte) y el modelo de tres factores (edad-período-cohorte) estimados mediante mínimos cuadrados ponderados. Ésta parece una propiedad deseable y es por ello que el parámetro de identificabilidad (l) se obtiene escogiendo el modelo de tres factores que minimiza esta distancia.
Definamos q (l) = (µ , a , b , g ) como el vector de parámetros del modelo edad-período-cohorte que depende de l según (4). Si llamamos qc al vector de parámetro del modelo edad-período (es decir, q[l] con g = 0) y q y θ P de forma similar para la edad y el período, la función de penalización12 es
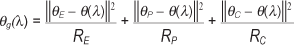
donde || || 2 es el cuadrado de la distancia euclídea entre los dos conjuntos de parámetros estimados, l es el parámetro de no identificabilidad y RE, RP, y RC es la media residual de la suma de cuadrados de cada modelo de dos factores.
Decarli y La Vecchia13 proponen una solución similar, estimando los modelos mediante regresión de Poisson, y facilitan unas macros de GLIM para calcular el parámetro l. La única diferencia con el método descrito por Osmond y Gardner radica en que la media residual de la suma de cuadrados se sustituye por la devian-ce residual del modelo dividida por los grados de libertad13.
Tendencia lineal (drift) y curvaturas
Otra forma de evitar el problema de no identificabilidad es limitar el análisis a los efectos, o sus combinaciones lineales, que permanecen constantes con cualquiera de los modelos de tres factores. A este método se le llama también de funciones estimables. Si se identifican estas funciones, no es necesario realizar ninguna asunción adicional para restringir los parámetros ya que cualquiera de los modelos máximo-verosímiles permite obtener los mismos resultados sobre ellas8,15. Holford8 mostró que, entre otras, ai + bj , ai gk y bj + gk (por error, en la referencia 8 figura como estimable ai + gk ) son funciones estimables. Clayton y Shifflers15 utilizan el resultado anterior para separar dos componentes lineales estimables. Uno es el efecto lineal de la edad y otro, que denominan tendencia lineal (drift), es la combinación no separable de los efectos lineales del período y la cohorte15. A partir del coeficiente de tendencia lineal se puede calcular, como índice resumen, el porcentaje de incremento promedio anual en la tasa. Para ello se usa la fórmula 100(exp[t] 1), donde t es el coeficiente asociado a la tendencia lineal en períodos o cohortes. Para su estimación se introduce en el modelo una variable cuantitativa que codifica los períodos (i) o cohortes (k), según la definición de la fórmula (1). Se obtiene el mismo resultado con i o k puesto que el efecto lineal del período o de la cohorte no es separable. A partir del error estándar de t se puede calcular un intervalo de confianza (k) para el porcentaje de incremento promedio anual.
Además de los efectos lineales, Holford6 propone realizar una estimación de la curvatura de los efectos de cada uno de los tres factores (el autor utiliza indistintamente los términos «curvatura» y «desviación» que debe entenderse como desviación de la linealidad). Para ello, estima los parámetros para un efecto y a continuación realiza una regresión lineal con estas estimaciones. Tras esto, calcula la curvatura como el residual entre el parámetro y la predicción de la regresión lineal. Esta curvatura es también una función estimable (es decir, independiente de la restricción utilizada) y permite interpretar la forma de la curva del efecto de período (p. ej., si es cóncava o convexa) o identificar en qué momentos se producen cambios importantes en la tendencia, pero no permite una interpretación en términos de riesgo relativo. Este análisis se realiza por separado para el efecto período y cohorte, pues las respectivas curvaturas sí son identificables. La principal limitación de estas curvaturas es la dificultad en su interpretación, por estar despr ovistas de la tendencia lineal.
Ejemplo práctico
A continuación pr esenta re mos dos ejemp los para ilustrar los métodos mencionados anteriormente. Se ilustrará gráficamente el análisis de la tendencia lineal y las curvaturas según el método de Holford y los parámetros obtenidos mediante las funciones de penalización según el método de Decarli y La Vecchia. Estos últimos se pueden interpretar como una modificación de los parámetros estimados mediante un modelo con los tres factores en los que en cada efecto se ha corregido teniendo en cuenta la relación lineal entre ellos mediante el parámetro de no identificabilidad l. Se pueden solicitar a los autores las funciones implementadas en S-Plus o R que realizan los cálculos.
Analizaremos los datos de mortalidad de Cataluña16 del período 1975-1998 para el cáncer de pulmón y mama en las mujeres mayores de 34 años. Los datos se han agrupado en períodos de 5 años y en quinquenios de edad (35-39, 40-44,..., 80-84, 85+) para cada uno de los dos tumores seleccionados.
En un primer análisis estadístico puede apreciarse claramente que para ambos tumores el modelo de 3 factores ajusta mucho mejor que cualquiera de los modelos de dos factores (tabla 1). El test de la razón de verosimilitudes es muy significativo y el AIC menor corresponde al modelo con tres factores. Si comparamos entre sí los modelos de dos factores mediante el AIC, el edad-cohorte es mejor en el caso de cáncer de pulmón y el edad-período para el cáncer de mama.
En el caso del cáncer de pulmón, la tendencia lineal asociada a período o cohorte (drift) no es significativa, el porcentaje de incremento anual promedio estimado es de 0,10 (IC del 95%: 0,21 a 0,19) y el AIC del modelo con la tendencia lineal aumenta respecto al modelo que sólo contiene edad. Los modelos de 2 factores mejoran el ajuste y ello indica que, a pesar de no existir un aumento lineal, hay curvatura, mayor en las cohortes que en el período según se deduce del AIC y de los tests de la razón de verosimilitudes. En la figura 2 se presenta la evolución de las tasas de mortalidad específicas por grupos de edad al cambiar la cohorte de nacimiento. Puede apreciarse que la pendiente creciente en las tasas aumenta de manera más pronunciada en las edades más jóvenes, que corresponden a individuos nacidos en cohortes más recientes, mientras que el aumento es menor en las edades mayores, que corresponden a cohortes más antiguas. Esto es característico de un efecto cohorte.
| Figura 2. Tendencia de la incidencia específica por edad de cáncer de pulmón y mama en mujeres en Cataluña en el período 1975-1978. |
 |
Para continuar la interpretación de los datos es útil realizar el análisis gráfico del modelo edad-período-cohorte mediante las técnicas mencionadas en los apartados anteriores. En la figura 3 podemos observar las curvaturas (o desviaciones) de Holford, junto con los parámetros de las cohortes corregidos por el método de Decarli y La Vecchia y los parámetros de las cohortes puros, es decir, asumiendo los parámetros del período nulos, y a su derecha se representan para el efecto período. En este tipo de representación se suele tomar una cohorte y un período centrales como referencia, por una cuestión puramente visual, que toman un riesgo relativo basal de 1. La impresión visual para el cáncer de pulmón en mujeres es que no hay gran variación en la mortalidad de las diferentes cohortes hasta las nacidas en 1950, momento en el que las tasas de mortalidad aumentan considerablemente. Este hecho se ratifica observando las curvaturas de Holford, pues en esos mismos períodos se observa una desviación de la linealidad importante. Este efecto cohorte nos indica que en las mujeres más jóvenes se observa un aumento de la mortalidad por cáncer de pulmón, hecho que podría ser atribuido al aumento del hábito tabáquico.
| Figura 3. Estimación de los efectos período y cohorte según el método de Decarli y La Veccia, del efecto exclusivo (ignorando el otro) y delas curvaturas según el métod de Holford. |
 |
En cuanto al cáncer de mama, parece que el efecto período es más importante que el efecto cohorte. En este tumor la tendencia lineal (drift) sí es significativa, y el porcentaje promedio anual de incremento estimado es de 1,04 (IC del 95%: 0,94-1,15). El modelo edad-período tiene un AIC bastante menor que el edad-cohorte, aunque claramente el modelo de tres factores es el que mejor se ajusta a los datos. En la figura 2 puede apreciarse cómo, para cada grupo de edad, a medida que se cambia de cohorte, la pendiente es creciente en los primeros períodos y se da un descenso en el último período. Estos cambios de tendencia afectan a todos los grupos de edad de manera similar, algo característico de un efecto período. En la figura 3 también se aprecia que la curvatura del efecto período es mayor que la del efecto cohorte, con un cambio brusco en la tendencia ascendente en la mortalidad en el último período, en el que desciende. Podríamos especular que esta reducción de la mortalidad en los últimos períodos se debe a la introducción de mejoras en los tratamientos tal como se ha atribuido en otros países17, puesto que es pronto para observar efectos de los programas de cribado poblacional que se han instaurado en Cataluña.
Debe tenerse en cuenta que, en ambos ejemplos, el efecto cohorte estimado mediante el método de Decarli y La Vecchia es prácticamente igual al efecto cohorte puro. Interpretar este método de manera aislada nos podría inducir a pensar que en ambos casos el efecto cohorte es el predominante.
Discusión
En este trabajo se han ilustrado las dos metodologías más usadas en el análisis de efectos edad-período-cohorte: los métodos de penalización y los de funciones estimables. Nuestra recomendación es emplear los métodos basados en funciones estimables y, en todo caso, no analizar los modelos con los métodos de penalización de manera aislada. El motivo principal radica en el hecho que los métodos basados en funciones de penalización tienden a atribuir la tendencia a un efecto cohorte exclusivo, incluso en casos en los que otros métodos muestran que el efecto principal es el período, como ocurre en el ejemplo mostrado del análisis de la mortalidad por cáncer de mama. Este fenómeno ha sido bien documentado en el trabajo de Robertson et al18 en el que comparan éstos y otros métodos de análisis simulando datos coefecto cohorte o pe-ríodo y comparando los resultados. Holford19 también menciona este fenómeno y lo atribuye al hecho de que al haber más términos de cohortes que de períodos, los primeros adquieren mayor peso en las funciones de penalización.
Aunque los dos métodos tratados en esta nota son los más usados para resolver el problema de no identificabilidad, existen otras posibles soluciones, aunque ninguna con resultados del todo satisfactorios. Sin querer ser exhaustivos, citaremos algunos. Robertson y Boyle11 proponen un método que precisa los datos individuales (no agrupados, como los ejemplos ya comentados) para poder construir una tabla de tres entradas (edad, período y cohorte). El problema es que este método infraestima el efecto en las cohortes jóvenes y lo sobreestima en las viejas18. Lee y Lin14 proponen un método que impone una estructura de serie temporal a los efectos. Esta aproximación considera que los efectos cohorte son estocásticos en vez de deterministas. Otra alternativa, menos empleada, es el procedimiento de las medias pulidas (mean polish) propuesto por Selvin20 y aplicado recientemente por Shahpar y Li4. Con este método se realizan estimaciones no máximo-verosímiles, evitando así el problema de no identificabilidad a costa de asumir que el efecto de cohorte es toda interacción no multiplicativa entre la edad y el período. Moolgavkar et al21 intentan evitar el problema de no identificabilidad introduciendo efectos no lineales pero la estimación de parámetros es difícil e inestable. Finalmente, Zheng et al1 utilizan regresión polinómica y con splines, métodos que proporcionan unos parámetros estimables pero de difícil interpretación.
En conclusión, el problema de los modelos edad-período-cohorte en la actualidad sigue sin tener una solución definitiva a pesar de los múltiples enfoques que se han probado. Nuestra recomendación, después de revisar los diferentes métodos propuestos, es que debe evitarse el análisis exclusivo mediante los métodos basados en funciones de penalización (Osmond y Gardner12 o de Decarli y La Vecchia13) ya que tienden a ensalzar sistemáticamente el efecto cohorte por lo que es más apropiado utilizar modelos basados en funciones estimables para ayudar a identificar qué efecto es más importante (Clayton y Schifflers10 o Holford6).
Agradecimientos
El autor agradece al Dr. Esteve Fernández la revisión y los comentarios críticos realizados a una versión final de este manuscrito. También al Registro de Mortalidad de Cataluña que ha facilitado los datos que se presentan en los ejemplos.
Bibliografía
1. Zheng T, Holford TR, Chen Y, Ma JZ, Flannery J, Liu W, et al. Time trend and age-period-cohort effects on incidence of thyroid cancer in Connecticut. Int J Cancer 1996;67:504-9. [ Links ]
2. Takahashi H, Okada M, Kano K. Age-period-cohort analysis of lung cancer mortality in Japan, 1960-1995. J Epidemiol 2001;11:151-9. [ Links ]
3. López-Abente G, Pollán M, Vergara A, Moreno C, Moreo P, Ardanaz E, et al. Age-period-cohort modeling of colorectal cancer incidence and mortality in Spain. Cancer Epidemiol, Biomarkers Prev, 1997;6:999-1005. [ Links ]
4. Shahpar C, Li G. Homicide mortality in the United States, 1935-1994: age, period and cohort effects. Am J Epidemiol 1999;150:1213-22. [ Links ]
5. Castilla J, Pollán M, López-Abente G. The AIDS epidemic among Spanish drug users: a birth cohort-associated phenomenon. Am J Public Health 1997;87:770-4. [ Links ]
6. Mason WM, Fienberg SE, editores. Cohort analysis in sociological research: New York: Springer-Verlag, 1985. [ Links ]
7. Moller H. Trends in incidence of testicular cancer and prostate cancer in Denmark. Human Reprod, 2001;16: 1007-11. [ Links ]
8. Holford TR. The estimation of age, period and cohort effects for vital rates. Biometrics 1983;39:311-24. [ Links ]
9. Holford TR. Age-period-cohort analysis. In: Gail MH, Benichou J, editors. Encyclopedia of epidemiologic methods. West Sussex: Wiley, 2000; p. 17-35. [ Links ]
10. Clayton D, Schifflers E. Models for temporal variation in cancer rates I: age-period and age-cohort models. Stat Med 1987;6:449-67. [ Links ]
11. Robertson C, Boyle P. Age, period and cohort models: The use of individual records. Stat Med 1986;5:527-38. [ Links ]
12. Osmond C, Gardner MJ. Age, period and cohort models applied to cancer mortality. Stat Med 1982;1:245-59. [ Links ]
13. Decarli A, La Vecchia C. Age, period and cohort models: a review of knowledge and inplementation in GLIM. Riv Stat Applicata 1987;20:397-410. [ Links ]
14. Lee WC, Lin RC. Autoregressive age period cohort models. Stat Med 1996;15:273-81. [ Links ]
15. Clayton D, Schifflers E. Models for temporal variation in cancer rates II: age-period-cohort models. Stat Med 1987; 6:468-81. [ Links ]
16. Registre de Mortalitat de Catalunya. Servei d'informació i Estudis, Direcció General de Recursos Sanitaris. Barcelona: Departament de Sanitat i Seguretat Social, 1999. [ Links ]
17. Peto R, Boreham J, Clarke M, Davies C, Beral V. UK and USA breast cancer deaths down 25% in year 2000 at ages 2069 years. Lancet 2000;355:1822. [ Links ]
18. Robertson C, Gandini S, Boyle P. Age-period-cohort models: A comparative study of available methodologies. J Clin Epidemiol 1999;52:569-83. [ Links ]
19. Holford TR. Understanding the effects of age, period, and cohort on incidence and mortality rates. Annu Rev publ Health 1991;12:425-57. [ Links ]
20. Selvin S. Statistical analysis of epidemiologic data. New York: Oxford University Press, 1996; p. 103-25. [ Links ]
21. Moolgavkar SH, Stevens RG, Lee JAH. Effect of age on incidence of breast cancer in females. J Natl Cancer Inst 1979;62:493-501. [ Links ]














