INTRODUCCIÓN
Para poder calcular el tamaño de las llamadas “poblaciones ocultas” (aquellas difíciles de identificar, generalmente por tener características estigmatizadoras o ilegales), los métodos más utilizados son los llamados métodos indirectos. Estos, parten de la premisa de que las fuentes de datos disponibles no son completas, por lo que realizan diferentes cálculos para estimar la prevalencia real de la población1,2.
Existen diversos métodos indirectos, de sencilla aplicación y que pueden ayudar al investigador a conocer el tamaño de estas poblaciones. El original publicado en 2017 por Revista Española de Salud Pública2 sobre estos métodos indirectos introducía en el conocimiento de cuatro de ellos: Captura-recaptura, Método Multiplicador, Poisson Truncado y Muestreo dirigido por participantes.
El propósito de este artículo es completar la revisión de este original con otros métodos muy útiles para obtener estimaciones de la prevalencia de poblaciones de difícil acceso: Método del indicador multivariado, Random walk, network Scale-up y métodos adaptativos geográficos.
MÉTODO INDICADOR MULTIVARIADO
Este método realiza estimaciones del tamaño de una población mediante la extrapolación de información de poblaciones en las que se dispone de datos (población de calibración) a la que queremos calcular (población objetivo). Y lo hace a través de variables de interés que están en ambas poblaciones3. Esto se realiza mediante la relación existente entre la variable de estudio y otras variables relacionadas con ella.
Para comprenderlo mejor, partamos de un ejemplo. Si deseamos estimar la prevalencia de usuarios de drogas en un país, necesitaríamos disponer de información de un conjunto de indicadores relacionados con el consumo de drogas (por ejemplo, número de personas en tratamiento por drogodependencia, número de arrestos relacionados con drogas, número de muertes relacionadas con drogas, etc.) en todas las regiones en las que se divide administrativamente dicho país. A estos indicadores se les denomina predictores. Por otro lado necesitaremos conocer la prevalencia de consumo de drogas en algunas de estas regiones (poblaciones de calibración), a las que llamaremos puntos de anclaje3,4. Una vez conocida esta información, se establece una relación entre los puntos de anclaje y los predictores mediante una regresión de mínimos cuadrados3, permitiendo así estimar la prevalencia de consumo de drogas en las regiones que carecieran de esta información. Por último, se estimaría la prevalencia de consumo de drogas en todo el país mediante la suma de las estimaciones de las prevalencias regionales3.
Así, si disponemos de los datos completos de prevalencia de usuarios de drogas en la comunidad de Madrid, así como del número de personas que se encuentran en tratamiento por esta adicción, los arrestos relacionados o el número de muertes relacionadas con el consumo de sustancias, podría inferirse qué ocurre en otras comunidades en las que solo tenemos información parcial.
El punto clave de este método, por tanto, es realizar una correcta asociación entre la información que desea estimar (Ej: Número de usuarios de drogas) que sería nuestra “variable dependiente”, y los predictores (Ej: Número de personas en tratamiento por consumo de drogas, número de arrestos relacionados con drogas) en nuestra muestra de calibración, y que ésta sea transferible a todas las demás áreas4,5. Dicho de otra forma, si existe una relación entre el tamaño de una población y varios de sus indicadores, cuando no conozcamos este tamaño podremos valernos de los indicadores para inferirlo.
Este método no está exento de limitaciones. La asunción de la existencia de una relación lineal entre las prevalencias no observadas y los indicadores observados es el principal componente a valorar3. Además, otros factores pueden influir en los indicadores y pueden invalidar el supuesto de linealidad. Siguiendo con el ejemplo antes expuesto, se podría pensar que un aumento en la prevalencia de usuarios de drogas llevaría a un número creciente de adictos en tratamiento; sin embargo, el número de adictos en tratamiento puede verse restringido por la capacidad de los servicios de tratamiento. Para la bondad en la aplicación de este método, debe analizarse con cuidado la comparabilidad de los indicadores entre la población objetivo y la de calibración. En este mismo sentido, la confiabilidad y la validez de los puntos de anclaje son de importancia crucial para la estimación; si las estimaciones se obtienen a través de técnicas diferentes, o se refieren a periodos de tiempo diferentes, pueden representar diferentes poblaciones de usuarios de drogas y esto influiría en la validez de la estimación nacional3. Esta validez se puede mejorar aumentando el número de puntos de anclaje4, lo que además es útil teniendo en cuenta que el número de puntos de anclaje debe ser superior al número de indicadores, pues de lo contrario no es posible establecer una regresión entre los mismos4.
Debemos tratar de minimizar todas estas limitaciones a la hora de aplicar este método, ya que, aunque se trate de inferencias y estimaciones y estas siempre lleven implícito un margen de error, nuestro objetivo es hacer dicho error lo más pequeño posible y obtener una estimación válida y exhaustiva.
Existen múltiples ejemplos prácticos de la aplicación de esta metodología que pueden ayudar a comprender mejor la misma3,4.
MÉTODO RANDOM WALK
Es una técnica que para calcular el tamaño de la población objetiva, contacta con sus miembros a través de nominaciones de sus contactos sociales6. Los reclutadores comienzan por seleccionar varias personas como informantes (por ejemplo, consumidores de drogas); este informante les ofrece una lista de posibles personas a riesgo, entre las cuales los reclutadores seleccionan aleatoriamente a una de ellas, que de nuevo les ofrece una lista de personas a riesgo entre sus contactos, de las cuales se selecciona aleatoriamente una, que ofrecerá otra lista de personas a riesgo, y así sucesivamente (figura 1).
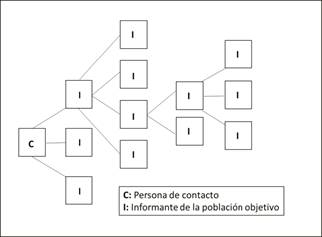
Fuente: Elaboración propia. Basado en el modelo expuesto en Bell DC, Erbaugh EB, Serrano T, Dayton-Shotts CA, Montoya ID. A comparison of network sampling designs for a hidden population of drug users: Random walk vs. respondent-driven sampling. Soc Sci Res. 2017;62:350-361.
Figura 1. Diseño de un estudio de estimación de prevalencias según el método Random-walk.
A medida que el Random-walk se introduce en la población, cada persona de la población objetivo tiene una probabilidad estadísticamente no nula de ser seleccionada7.
Es un método incluido dentro de los basados en redes sociales (entendiendo este término como el conjunto de individuos con algún tipo de relación personal o interés en común). Es muy similar al RDS (Respondent driven sampling) expuesto en el artículo anterior2, pero su principal diferencia radica en que mientras en el método RDS los propios participantes nominan a los participantes de la siguiente ola y son compensados mediante diversos incentivos, en el método random walk el participante facilita un listado de personas de su red social que cumplen los requisitos para ser elegidos, y es el propio investigador quien elige aleatoriamente entre las personas de esa lista al siguiente participante.
Si el método random walk es implementado correctamente puede producir una muestra altamente representativa de la población objetivo7. Sin embargo, existe la posibilidad de que aparezca un sesgo de muestreo si la población contiene múltiples redes que no están conectadas entre sí7. Si todos los miembros de la población estuviesen interconectados (situación ideal pero no real), todos serian alcanzables a través de una sola semilla. Pero al existir grupos aislados pequeños, estos se escapan del marco de muestreo. Para reducir este sesgo se deben seleccionar múltiples “semillas” en diferentes redes7. En el ejemplo expuesto, para calcular el número de usuarios de drogas en una ciudad no bastaría con partir de uno solo. Tendríamos que buscar varios, distribuidos por diferentes zonas de la misma.
Otros posibles sesgos ocurren cuando el informante no se siente seguro a la hora de divulgar información acerca del comportamiento de sus redes sociales, o se siente especialmente motivado a hacerlo por cualquier circunstancia, ofreciendo información no veraz en cualquiera de los dos casos. Para minimizar este sesgo, los investigadores deben involucrarse con los sujetos y reclutarlos personalmente, aumentando la confianza que los participantes depositan en ellos, aunque esto requiera una mayor inversión de tiempo y recursos7.
THE NETWORK SCALE-UP METHOD
Se trata de otro método basado en redes sociales. Este método asume que las redes sociales de las personas son representativas de la población general en la que viven8,9. A partir de este supuesto, se observa el número de individuos que presentan una característica en la red social de una persona y se extrapola esta información a la población general.
Siguiendo con el ejemplo de los usuarios de drogas, si un individuo (perteneciente a la población objetivo o no) conoce a 300 personas, y sólo dos de ellas son usuarias de drogas, asumimos que en la población general esta proporción se mantendrá igual, es decir 2/300 personas serían usuarias de drogas8. Combinando la información sobre las redes sociales de muchas personas, podremos determinar el tamaño de la población oculta con una sencilla fórmula (ver figura 2) que consiste básicamente en dividir el número de personas que cumplen los criterios de la población oculta a estudiar conocidos por los sujetos entrevistados entre la suma de sus redes sociales multiplicado por el tamaño de la población general.
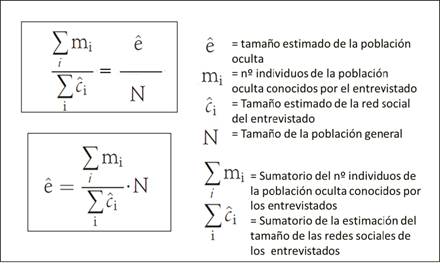
Fuente: Elaboración propia, basado en el modelo del artículo de Bernard HR, Hallett T, Iovita A, Johnsen EC, Lyerla R, McCarty C, et al. Counting hard-to-count populations: the network scale-up method for public health. Sex Transm Infect. 2010;86 (Suppl 2):ii11-ii15.
Figura 2. Fórmula utilizada para la estimación del tamaño de la población oculta según el método Network Scale up.
La dificultad principal estriba en la capacidad de estimar la verdadera red social de cada persona10. Para ello existen dos métodos:
a) Método de la población conocida. Mediante esta técnica se intenta cuantificar el número de sujetos conocidos por las personas entrevistadas de entre varios grupos de población cuyo tamaño se conoce a priori, incluyendo poblaciones diferentes a la población oculta de interés8,10. Por ejemplo, si se quiere conocer la población de diabéticos mayores de 18 de años en España, con esta técnica se preguntaría a los sujetos con esta enfermedad cuántos de sus contactos la padecen. Si un diabético dice conocer a 22, y se sabe que en España hay aproximadamente 5,3 millones de diabéticos mayores de 18 años y una población total de 38,2 millones de españoles con esa edad11 se asume con una sencilla “regla de tres” que el número de personas conocidas por el entrevistado es de 159. Para reducir la varianza de la estimación, se recomienda indagar en al menos 20 subpoblaciones diferentes8.
b) Método de la suma. Mediante esta técnica se intenta cuantificar el número de personas que cumplen los criterios de la población de estudio en cada uno de sus grupos sociales: familia, amigos, vecinos, compañeros de trabajo, etc. La suma de personas referidas en estas categorías nos proporcionaría una estimación del tamaño de su red personal8,10. Este método es más sencillo, pero requiere de una buena definición de las categorías, procurando no olvidar ninguna, pues de lo contrario caeríamos en una infraestimación, y que sean excluyentes entre sí, para no contabilizar un mismo conocido en dos categorías diferentes, lo que conduciría a una sobreestimación8.
Una vez calculado el número de personas que conoce el entrevistado (denominador), pasamos a preguntar por nuestra variable de interés: Número de personas usuaria de drogas de su red social (numerador). Continuando con el ejemplo inicial, si el entrevistado conoce a 2 personas usuarias de drogas, y su red social la componen 159 personas (estimado con el método de la población conocida), suponemos que 2/159 personas en España son usuarias de drogas. Según el INE11, en España hay 46,5 millones de personas, por lo que estimamos que existen 584.906 personas usuarias de drogas en España.
Este cálculo se repite con numerosos entrevistados, y aplicando la fórmula de la figura 2, podemos tener una estimación del tamaño de la población oculta.
Al igual que el resto de métodos, este no está exento de sesgos; el principal de ellos es el llamado sesgo de trasmisión8, en el cual el entrevistado no conoce todos los aspectos de la vida de sus contactos, lo que ocurre frecuentemente; y más en nuestro caso en particular, cuando se trata de actividades socialmente estigmatizadas. Otro es el llamado sesgo de barrera8, el tener contactos entre la población de estudio puede depender de barreras físicas o sociales como la raza, la etnia, la ocupación o el lugar de residencia. Otro sesgo que nos podríamos encontrar sería el sesgo del recuerdo, en el cual, el entrevistado no puede recordar correctamente la cantidad de personas que conoce de una subpoblación, o no puede hacerlo en el marco de tiempo permitido por el estudio10.
A pesar de ello, es un método que también tiene numerosas ventajas: no pregunta directamente a los encuestados sobre sus características, sino por las personas que conoce que presentan dichas características, facilitando una enumeración anónima de contactos; esto hace que disminuya la carga del estigma en los entrevistados10. En segundo lugar, como no necesitamos entrevistar directamente a los miembros de una población oculta, sino a población general, podemos realizar técnicas de muestreo generales que son más baratas y fáciles de implementar10. Otra de las ventajas es que se puede usar para producir estimaciones para varias poblaciones ocultas diferentes simultáneamente y, además, puede aplicarse fácilmente a poblaciones de tamaño conocido, lo que nos serviría para valorar la validez del propio método12.
El Network scale-up es un método eficiente. Su capacidad para generar estimaciones precisas de estas poblaciones utilizando marcos de muestreo convencionales y técnicas de encuesta lo convierte en un método considerablemente más barato y rápido que las técnicas comúnmente utilizadas para estudiar poblaciones ocultas10. Debido a esto, se está utilizando en estudios en todo el mundo, y su uso se está ampliando cada vez más8,9,10,12,13. Es una de las técnicas más utilizadas actualmente en diferentes campos de la salud pública9,14,15.
MÉTODOS ADAPTATIVOS GEOGRÁFICOS
Los métodos adaptativos son aquellos que tras una muestra aleatoria inicial, van incluyendo participantes en función de sus respuestas y la información recopilada durante el estudio. En este caso en particular, esta adaptación se basa en la localización, ya que los investigadores usan relaciones geográficas entre personas para encontrar otras personas que incluir en la muestra.
Existen varios métodos adaptativos geográficos:
1) Método de la asignación adaptativa: el punto de partida es una muestra obtenida utilizando un diseño convencional, como el muestreo aleatorio simple o estratificado. Posteriormente se examina esta muestra en busca de evidencia de que algunas áreas geográficas exhiben más comportamientos de interés que otras, según los valores observados en algunas variables clave. Se continúa entonces el muestreo concentrándose en estas áreas16.
Siguiendo con el ejemplo de las anteriores metodologías, si queremos conocer el número de jóvenes que están en riesgo de convertirse en usuarios de drogas, se puede tomar una muestra aleatoria estratificada inicial, que mida las variables clave que, se sabe, indican el riesgo de inicio del consumo de drogas (absentismo escolar, creencias sobre los niveles normativos de las drogas…). A continuación, en áreas geográficas donde aparece una alta concentración de riesgo, se asignan más recursos de muestreo y se toma una muestra más grande para continuar el estudio16.
2) Muestreo adaptativo por conglomerados: al igual que en modelo anterior, se selecciona una muestra inicial con un diseño de muestreo convencional. Cuando encontremos un individuo que presente nuestra variable de interés, las unidades (casa, colegio, familia…) del vecindario de esa unidad se agregan a la muestra. Si, a su vez, un individuo de cualquiera de las unidades agregadas satisface la condición, se agregarán aún más unidades, y así sucesivamente16. Por ejemplo, un estudio de personas que consumen drogas podría comenzar tomando una muestra aleatoria de hogares. Siempre que se encuentre que un hogar contiene una persona usuaria de drogas, se tomarán muestras de las casas vecinas. Si a su vez cualquiera de estas casas contiene una persona usuaria de drogas, se tomarán muestras de las casas vecinas, y así sucesivamente17.
Sin embargo, estos métodos tienen una limitación importante: Ambos parten de un muestreo aleatorio, y por lo tanto podemos encontrar que las variables de interés (consumo de drogas, VIH, prostitución, etc.) propias de algunas poblaciones ocultas, que no se distribuyen aleatoriamente en la población, sean de difícil detección en este primer paso.
Además de todos los métodos descritos tanto en este artículo como en el anterior2, existen muchos más pero de mayor complejidad estadística y metodológica18,19,2, que quedan fuera de los objetivos de este artículo.
CONCLUSIONES
Como hemos podido comprobar tanto en este artículo como en el anterior2, disponemos de diferentes formas para estimar el tamaño de poblaciones ocultas, pero ninguna de ellas está exenta de limitaciones ni puede considerarse como el método ideal (anexo I). La elección de la técnica dependerá de los datos de los que dispongamos, del objetivo de nuestro estudio y del tipo de población a la que queramos acceder.
Además, siguiendo las recomendaciones de la literatura revisada para la estimación de la prevalencia de las poblaciones ocultas, lo más correcto sería aplicar varios métodos sobre la misma población evaluando cuidadosamente las limitaciones de cada uno de ellos y comparando los diferentes resultados obtenidos y su coherencia con la realidad. Finalmente, señalar que los métodos desarrollados en este y en el anterior artículo2 pueden ser muy útiles integrados en sistemas de vigilancia de poblaciones ocultas. La estimación repetida y periódica del tamaño de estas poblaciones, aun con las debilidades señaladas, puede ser una excelente herramienta para describir tendencias.















