Introduction
The Body Mass Index (BMI)1 is used to classify individuals into to certain categories in conventional quickly and practically ranges2. BMI is used worldwide because it is considered an important index of mortality (risk factor)3. When the BMI increases or decreases from the range of normality there is a reduction of life expectancy4,5. In fact, increasing BMI above the normal range raises the risk of diseases such as type 2 diabetes, cardiovascular disease, joint diseases, hormonal disorder and cancer6-8. In addition, increased BMI also increases the risk of menstrual dysfunction in women of childbearing age, difficulty in conceiving, and complications in pregnancy for both mother and child. By contrast, an underweight index below 18.5kg/m2 is associated with various diseases, including anorexia nervosa, amenorrhea and osteoporosis4,9,10. Nowadays, it is important to acknowledge that BMI does not distinguish whether the change in weight is due to the amount of muscle mass, bone mass, water content or fat accumulation2,11,12. This classification is also fixed and is not adaptable to all adults, especially athletes or the elderly13. The established BMI categories are not specific enough because, taking two individuals of the same height; their classifications are based only on the variability of the mass, without considering the body composition12,14-16. The body surface area obtained by using the square of the height is only an approximation of the actual body surface area and can differ substantially between individuals with the same height17-19. This is because they have different body compositions, which differentially affect body volume. Considering, on the other hand, two people having the same body volume; the person with the higher fat content will have a lower body surface area, since the ratio between the volume and the surface area increases in relation to the increasing fat content, and vice versa.
The aim of this study is to propose a new index without altering the structural meaning, the units of measurement and the physical dimensions of BMI can provide more information, at least on the lipid component.
Material and methods
The study with 108 patients, including the informed consent procedure, was approved by the Ethical Committee of University of Milan (Italy). Data were collected and processed with the help of DIES4, a program that through anthropometric measurements calculates the classic BMI, the new BMI-BFMNU, volume, surface and body pseudospessore20.
The classic BMI is calculated using the formula:
Therefore BMI can also be calculated as density* (volume/height2). As height square is obviously a surface area, but if we use the real surface of body instead of height square, we can calculate BMI-BFMNU as follows:
The body Volume/body Surface corresponds to the new size that is the pseudospessore. The term pseudospessore was not translated because it was misleading. We used a term that gave the idea but deviate from everything known, as it is totally new:
The “pseudospessore” is used in the BFMNU method for the evaluation of the fat component:
Volume [dm3] = sum of the partial volumes of regular solids (cylinders, truncated cones, spheres, etc.) obtained from anthropometric measures.
Surface [m2] = sum of the surfaces of the partial volumes (from which must be subtracted the contact surfaces between adjacent partial volumes), obtained from the anthropometric measures.
Results
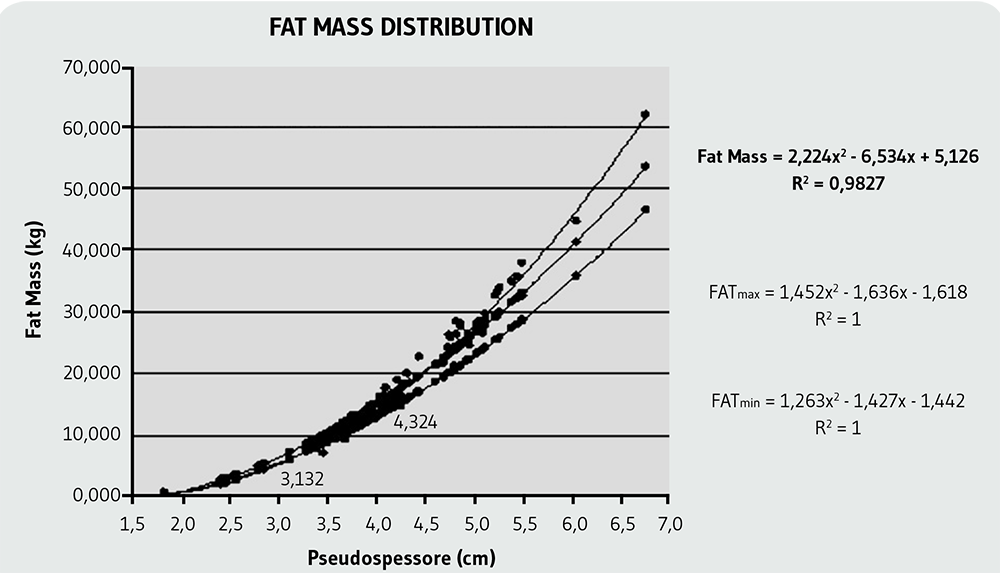
Figure 1 shows the correlation between fat mass and “body-thickness” (“pseudospessore”) demonstrating a strong correlation (R2=0.9827) with the measured values. The normal range and the top and bottom limits for the BMI-BFMNU was determined by taking a sample of patients considered “normal” as per the classic BMI (between 20 and 25kg/m2). The lower-limit curve for the obese range was determined using a sample with traditional BMI≥30kg/m2 and the upper limit curve of the underweight range using a sample with BMI≤17kg/m2. In addition, these two ranges were subdivided into intermediate intervals.
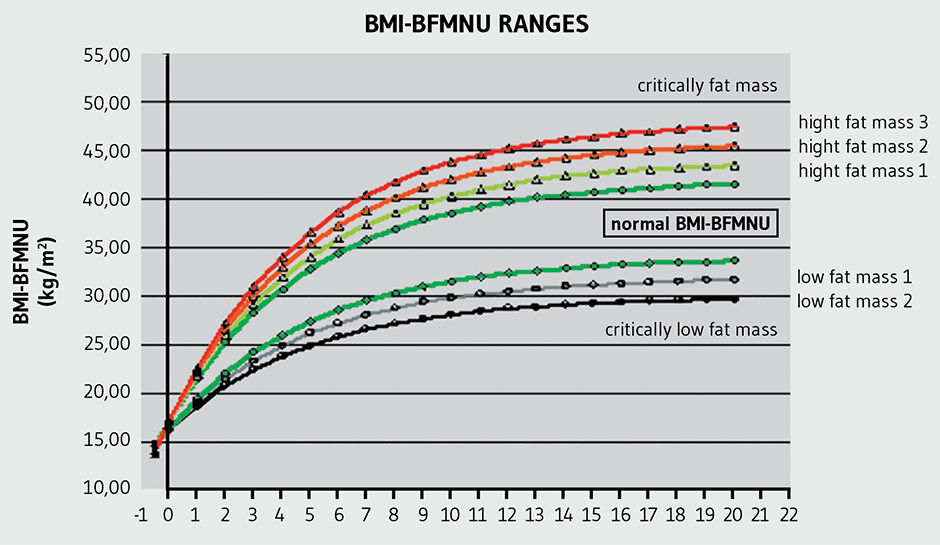
The normal ranges explained above are related to the adult population aged ≥20 years. As mentioned previously, the ranges for individuals below 20 years are established by curves (Figure 2) in function of the age being the following normal range:
As can be seen from the curves, the point of origin coincides with the beginning of the fetal stage and the birth interval has a width so small that they cannot distinguish between the obese and underweight ranges. In the table of study individuals, the normal ranges are represented for each of them according to their age (See Tables AM1 and AM2 in additional materials: http://www.renhyd.org/index.php/renhyd/article/view/1161/733).
Discussion
The relationship between volume and surface area is present in any definition of BMI. From a dimensional point of view, this ratio provides the value of a length (length3/length2 = length). This length was defined for the first time as pseudospessore21,22.
As expected, the BMI-BFMNU features new normal ranges. This was due to the fact that in the calculation of BMI-BFMNU, the patient's real body surface appears in the denominator, instead of the surface obtained as the square of the height. The new values of BMI-BFMNU do not only give general information on the structure (height) but provide quantitative information on the body fat composition as determined by the volume/surface area (pseudospessore).
From a structural point of view, the link with the fat component of the body was indicated by the ratio between the volume and the real surface for any age. While the classic BMI, having as denominator the square of the height, depends on the age and height, BMI-BFMNU depends only on the age. A good example is a developing child. During this phase, the individual grows in height, weight and surface. Although, the development in height produces a variation of the volume and the surface. However if their ratio (pseudospessore) increases, the individual tends towards being “fat” and, if vice versa, the ratio decreases the individual tends towards being “lean”. This statement can be confirmed by the comparison between the BMI and BMI-BMNU performed on a sample of patients. Although, patients 29 and 32 (Table AM2) are both classified as normal, falling into the lower limit of the classic BMI, the BMI-BFMNU of these patients are located into the normal range, which means that they are moving to the higher fat mass. Patient 19 (Table AM2) was classified as strongly underweight according to BMI, but was about normal for BMI-BFMNU; this means that the underweight is not due to a lack of body fat mass but to other components. Patients 38 (Table AM1) and 7 (Table AM2) were classified as overweight, while BMI-BFMNU was placed in the normal range; similarly to the previous case, the overweight condition was not due to the body fat component but to other factors. Finally, the patient that shows the greatest discrepancy between the two BMI classifications, was patient 1 (Table AM2), for whom according to the classic undefined BMI, the BMI-BFMNU falls into the upper limit of the normal range. It should be emphasized that being classified in the normal range of the BMI-BFMNU means that there was an appropriate amount of body fat in relation to the overall body mass, information that the older BMI did not provide.
Therefore, if a patient was classified as overweight according to the classical BMI and normal according to the BMI-BFMNU, if they decrease their mass to return to normal (by the classical definition), they will decrease all the mass components, with the fat component decreasing by a lower percentage than the other components. The example of patient 4 (Table AM2), provides a point to be considered; although the patient presents a minimal discrepancy between the classical BMI, which was slightly above normal, and BMI-BFMNU, which was normal even though slightly below the upper limit, they show an incongruous lipid component. The incongruity lies in the fact that the lipid component was certified in the classic BMI as upper the normal range, while in the BMI-BFMU it appears just below the normal.
A possible interpretation of every incongruities is the objective difficulty of using anthropometric measurements. Particularly in children, an error made in the anthropometric measures produces an even larger error in the calculation of the volume and the surface area compared to the same type of error in adults23,24.The error in the calculation of the lipid component in the total sample (n=108) was 11.7%, about 28% for patients under 13 years (n=18) and 7% for adults (n=90) respectively.
In fact, the use of BMI was contradictory in the literature; Frankenfield et al.8 observed limmitations of this parameter to detect obesity and predict body composition. Gallagher et al.16 showed that this index was age and sex dependent when used as an indicator of body fatness, but that it was ethnicity independent in black and white adults. De Lorenzo et al.7 concluded that adiposity rather than BMI could determine the metabolic risk. Furthermore, BMI was not useful to reflect body fat, changes in body composition that take place in the different periods of life or the sexual dimorphism characteristics of body adiposity25,26.
Conclusions
In conclusions, BMI-BFMNU has the following advantages: i) provides an instant indication of the body lipid content; ii) shows the influence of the fat component in the total body mass; iii) classifies individuals according to a uniform criterion based on lipid content regardless of their heights; iv) represents an additional tool for the evaluation of dyslipidemic disorders; v) supports the preparation of optimal personal nutritional plans including patients and athletes; and vi) its value is related to the age while the BMI depends on height and weight.